2.3. Сопротивление воздушной среды
2.3.1. Аэродинамические силы и моменты
На автомобиль, как и на всякое тело, движущееся в воздушной среде, действуют; аэродинамические силы. Равнодействующая всех элементарных аэродинамических сил называется полной аэродинамической силой Р w. Ее значение определяется по формуле
Р w = cwFq (2.5)
где сy - безразмерный коэффициент полной аэродинамической силы;
F - площадь миделева сечения, м2;
q - скоростной напор воздушного потока, Па.
Величина скоростного напора определяется по формуле
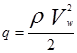
 (2.6)
(2.6)
где rв - плотность воздуха, кг/м3;
V w - относительная скорость воздушного потока, м/с.
Автомобили имеют довольно сложную форму, поэтому для них, в отличие от простых тел, вместо площади миделева сечения используется площадь их проекции на поперечную плоскость (рис. 2.2). Скоростной напор воздушного потока (q, Па) представляет собой величину динамического давления на корпус автомобиля, создаваемого воздушным потоком, омывающим автотранспортное средство. Точка приложения вектора полной аэродинамической силы (Р w) называется метацентром. автомобиля (или центром парусности). Метацентр в зависимости от аэродинамических свойств автомобиля может располагаться как внутри, так и вне автомобиля.
Проекция вектора полной аэродинамической силы на оси X, У и Z, проходящие через центр тяжести автомобиля, в общем случае дает три составляющие (см. рис. 2.2);
Р wx = cxF(r в Vw2/2) (2.7)
Р w у = c у F(r в Vw2/2) (2.8)
Р wz = czF(r в Vw2/2) (2.9)
Продольная составляющая (Р wx) полной аэродинамической силы называется лобовой аэродинамической силой или силой сопротивления воздуха.
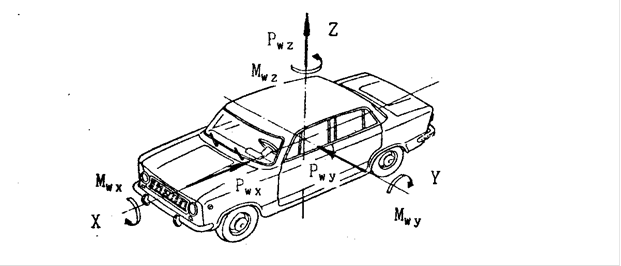 Рис. 2.2. Аэродинамические силы и моменты
Рис. 2.2. Аэродинамические силы и моменты
Поперечная составляющая (Р w у) называется боковой, а вертикальная (Р wz) подъемной аэродинамической силой.
Коэффициенты Сх, Су и С z называются безразмерными коэффициентами соответственно лобовой, боковой и подъемной аэродинамической силы. Указанные коэффициенты связаны между собой формулой:
cw2 = cx2 + c у2 + cz2. (2.10)
Как показывают эксперименты, центр тяжести автомобиля и его метацентр не совпадают, поэтому кроме указанных аэродинамических сил на автомобиль действуют и соответствующие аэродинамические моменты.
Результирующий момент всех элементарных аэродинамических сил относительно центра масс автомобиля называется полным аэродинамическим моментом. Его величина определяется по формуле
М w = mwFqbw. (2.11)
где mw - безразмерный коэффициент полного аэродинамического момента;
bw - характерный линейный размер по ширине, м.
Проекция вектора М w, на оси X, Y и Z дает три составляющие этого момента (см. рис. 2.2):
- аэродинамический момент крена;
М w х = m х F(r в Vw2/2)bw (2.12)
где mx - коэффициент аэродинамического момента крена.
- поворачивающий аэродинамический момент:
М wz = mzF(r в Vw2/2)bw (2.13)
где mz - коэффициент аэродинамического поворачивающего момента.
- опрокидывающий (продольный) аэродинамический момент:
М w у = m у F(r в Vw2/2)lw (2.14)
где m у - коэффициент опрокидывающего аэродинамического момента;
- lw - характерный линейный размер автомобиля по длине.
Связь между коэффициентами аэродинамических моментов выражается формулой:
mw2 = mx2 + m у2(lw / bw)2 + mz2 (2.15)
В качестве характерного линейного размера по ширине (bw) принимают обычно расстояние между правыми и левыми колесами автомобиля, т.е. его колею, а в качестве характерного размера по длине (lw) - базу автомобиля, т.е. расстояние между передним и задним мостом.
При расчетах аэродинамических сил и моментов следует учитывать изменения плотности воздуха в зависимости от температуры и атмосферного давления (см. формула 2.6).
3.3.2. Лобовая аэродинамическая сила и ее составляющие
При эксплуатации автомобилей из всех аэродинамических сил наибольшее значение имеет сила лобового сопротивления (Р wx). которая является одной из основных сил сопротивления движению автомобиля. При больших скоростях она становится главным фактором сопротивления движению. Так, например, для автомобиля "Волга" ГАЗ-3102 при скорости движения около 100 км/ч сила лобового аэродинамического сопротивления численно равна силе сопротивления качению. Значение лобовой аэродинамической силы часто выражают следующей формулой:
Р wx = kwFVw2, (2.16)
где kw = cx r в/2 - коэффициент обтекаемости автомобиля, Нс2/м4.
Мощность, необходимая для преодоления лобовой аэродинамической силы, описывается кубической параболой:
Nw = kwFVw3. (2.17)
Для легковых автомобилей площадь лобового сопротивления можно определить по приближенной формуле
F » 0,78brhr, (2.18)
где br , hr - габаритные ширина и высота автомобиля, м.
Приближенный расчет площади лобового сопротивления грузовых автомобилей производят по формуле
F » H к hr, (2.19)
где Нк - колея автомобиля, м.
Численные значения коэффициента обтекаемости и площади лобового сопротивления ряда отечественных марок и моделей автомобилей приведены в табл.1 Приложения 1.
Анализ аэродинамического сопротивления показывает, что лобовая аэродинамическая сила сопротивления складывается из 5 составляющих:
1) сопротивления формы;
2) сопротивления выступающих частей (сопротивление интерференции);
3) сопротивления поверхностного трения;
4) сопротивления внутренних потоков;
5) индуктивного сопротивления.
Сопротивление формы. Совокупность всех элементарных сил нормального давления воздуха, действующих на переднюю и заднюю наружные поверхности корпуса автомобиля, создает силу. которую принято называть сопротивлением формы. Величина указанной силы определяется разностью давлений воздуха на переднюю и заднюю стенки корпуса (рис. 2.3) и площадью их поверхности. При этом разница давлений в решающей степени зависит от формы кузова. Как показывают исследования, сопротивление формы составляет примерно 50...60% лобовой аэродинамической силы.
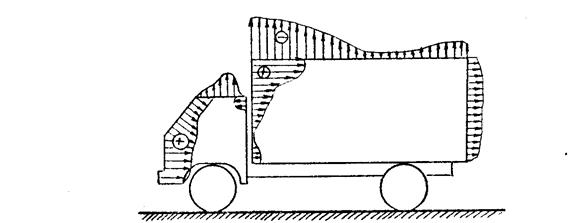 Рис.2.3. Распределение давления по поверхности автомобиля
Рис.2.3. Распределение давления по поверхности автомобиля
Сопротивление выступающих частей. Наличие на кузове выступающих частей (фар, подфарников, указателей поворотов, зеркал заднего вида, багажника и т.п.) создает дополнительное сопротивление. При этом все вышеуказанные элементы при установке на кузов создают гораздо большие аэродинамические сопротивления, чем те, которые они создают сами по себе, будучи отделенными от кузова. Это объясняется усилением перемешивания воздушных струй и турбулизацией воздушного потока, омывающего корпус автомобиля и его выступающие элементы. На долю сопротивления выступающих частей приходится около 15...17 % лобовой аэродинамической силы.
Сопротивление поверхностного трения. При обтекании автомобиля воздушным потоком вследствие трения о различные поверхности автомобиля скорость движения пограничных слоев воздуха, т.е. слоев, непосредственно примыкающих к стенкам, значительно снижается. Из-за разницы скоростей соседние слои воздушного потока, примыкающие к пограничным, тоже испытывают силу трения, вследствие чего скорость их движения также снижается. В результате в пристеночном слое воздушного потока, омывающего поверхности автомобиля, образуется градиент скорости. Наличие градиента скорости и сил трения приводит к дополнительному сопротивлению воздуха, называемому сопротивлением поверхностного трения.
По своей сути эта сила является результатом сложения всех касательных сил, прикладываемых к автомобилю. На долю силы сопротивления поверхностного трения приходится около 10 % лобовой аэродинамической силы.
Сопротивление внутренних потоков. Наряду с наружным обтеканием автомобиля некоторая часть воздушного потока проходит через внутренние полости (подкапотное пространство, салон, кабину водителя. кузов и др.), которые оказывают значительное сопротивление его продвижению. Как показывает анализ, сопротивление, испытываемое внутренними потоками воздуха, обусловливает примерно 8...10 % лобовой аэродинамической силы.
Индуктивное сопротивление. Некоторая часть воздушного потока, омывающая автомобиль, имеет вертикальную составляющую скорости, т. е. движется не только вдоль продольной оси кузова, но и одновременно в вертикальном направлении. Это способствует турбулизации воздушного потока и появлению дополнительного аэродинамического сопротивления, которое принято называть индуктивным. На долю индуктивного сопротивления приходится около 6...8 % лобовой аэродинамической силы.
2.3.3. Подъемная аэродинамическая сила
Образование подъемной аэродинамической силы Р wz; обусловлено перепадом давлений воздуха на автомобиль снизу и сверху (рис.2.3). Преобладание давления воздуха снизу над давлением сверху объясняется тем, что скорость движения воздушного потока, омывающего автомобиль снизу, гораздо меньше скорости потока. омывающего его сверху. Значение подъемной аэродинамической силы относительно мало и не превышает 1,5 % от веса самого автомобиля. Так, например, для автомобиля ГАЗ-3102 "Волга" подъемная аэродинамическая сила при скорости движения 110 км/ч достигает всего лишь 245 Н, что составляет около 1,3 % от собственного веса автомобиля. Спортивным автомобилям, движущимся с большими скоростями, придают такую форму, чтобы сила Р wz; была направлена не вверх, а вниз. т.е. прижимала его к дороге.
2.3.4. Боковая аэродинамическая сила
Боковая аэродинамическая сила возникает при обтекании автомобиля воздушным потоком под некоторым углом к его продольной оси. Наличие указанного угла в подавляющем большинстве случаев объясняется наличием бокового ветра, дующего под углом, а к продольной оси автомобиля (рис. 2.4).
|
|
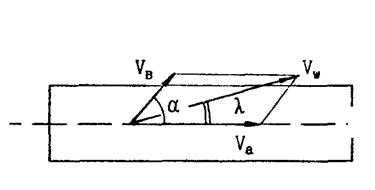
Рис.2.4. Обтекание автомобиля воздухом при боковом ветре:
l - угол натекания;
a - угол атаки ветра.
Если боковой ветер дует со скоростью Vв под углом a к продольной оси автомобиля, то результирующая скорость движения воздушного потока V w будет равна:
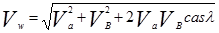 (2.20)
(2.20)
Из формулы (2.20), в частности, следует, что при угле атаки a = 0 (встречный ветер) скорость воздушного потока равна сумме скоростей автомобиля и ветра (V w = Va+ Vв), а при угле 180° (попутный ветер) разнице указанных скоростей (V w = Va – Vв).
Изменение скорости и направления бокового ветра приводит не только к изменению скорости воздушного потока, но и к изменению угла натекания воздушного потока (l). тангенс которого можно определить по формуле:
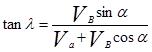 (2.21)
(2.21)
Как показывают испытания, действие бокового ветра особенно ощутимо для автотранспортных средств большой длины и высоты, т.е. автобусов и автопоездов.
2.3.5. Основные аэродинамические характеристики автомобиля
Основными характеристиками, дающими представление об аэродинамических свойствах автомобиля, являются распределение давления воздуха на наружной поверхности автомобиля (рис. 2.4) и зависимости коэффициентов аэродинамических сил и моментов от угла натекания воздушного потока (рис. 2.5): сх = f(l); су = f(l); с z = f(l); m х = f(l); mz = f(l).
Все указанные характеристики устанавливаются экспериментальным путем, как правило, на основе продувки автомобилей или их уменьшенных моделей (копий) в аэродинамической трубе.
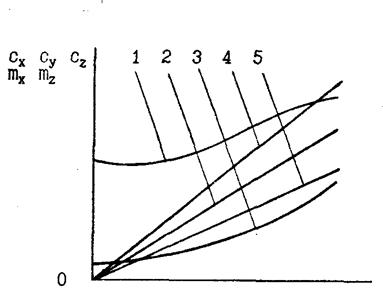
Как показывают аэродинамические эксперименты (рис. 2.5), при продольном движении воздушного потока (l = 0) значения Су, mz , mx равны 0. Это означает, что при отсутствии бокового ветра аэродинамическая сила Р w у и моменты этой силы (относительно осей Х и Z) не возникают. Важно также подчеркнуть, что увеличение угла натекания воздуха от 0 и выше приводит не только к возрастанию Су, но и к существенному повышению Сх и С z . Следовательно, боковой ветер вызывает не только появление боковой
Как показывают аэродинамические эксперименты (рис. 2.5), при продольном движении воздушного потока (l = 0) значения Су, mz , mx равны 0. Это означает, что при отсутствии бокового ветра аэродинамическая сила Р w у и моменты этой силы (относительно осей Х и Z) не возникают. Важно также подчеркнуть, что увеличение угла натекания воздуха от 0 и выше приводит не только к возрастанию Су, но и к существенному повышению Сх и С z . Следовательно, боковой ветер вызывает не только появление боковой аэродинамической силы, но и оказывает влияние на величину лобовой и подъемной аэродинамических сил.
|
Рис. 2.5. Основные аэродинамические характеристики автомобиля: 1 – C х=f(l); 2- C у = f(l); 3 – Cz = f(l); 4 - mx = f(l); 5 – mz = f(l)/ |
2.4. Внутренние силы сопротивления
2.4.1. Сопротивление двигателя
Работа ДВС сопровождается силами трения в цилиндропоршневой группе (ЦПГ) и подшипниках коленчатого вала, которые создают момент трения двигателя (Мтд). При этом особенно большие силы трения возникают между поршнями и гильзами цилиндров, на долю которых приходится почти половина всех механических потерь в двигателе. Это связано с весьма неблагоприятными условиями смазки ЦПГ и работой поршневых колец (особенно верхнего компрессионного) зачастую в условиях полусухой и даже сухой смазки. Условия смазки подшипников коленчатого вала более благоприятны, поэтому силы трения в них гораздо ниже. В целом потери на трение обусловливают около 65...75% всех механических потерь в двигателе (см. рис. 2.6). Величина момента трения зависит от литража, тактности, частоты вращения вала и теплового состояния ДВС.
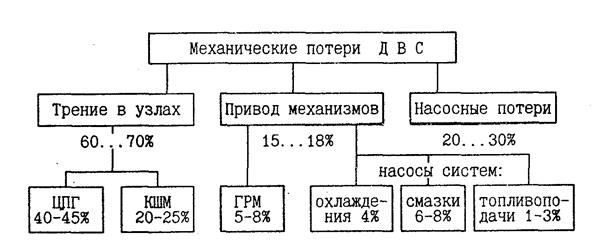
Рис. 2.6. Примерная структура механических потерь ДВС
Значительная часть сил сопротивления ДВС обусловливается работой газораспределительного механизма, а также насосов системы охлаждения, смазки и топливоподачи. Все они создают так называемый момент сопротивления механизмов двигателя (Ммд), на долю которого приходится около 15...20% суммарного сопротивления.
Определенная часть мощности ДВС затрачивается на засасывание, сжатие воздуха (или топливно-воздушной смеси) и выталкивание отработавших газов из цилиндров. Момент сопротивления газов (М rд), обусловливающий указанные насосные потери, составляет 15...20% всех механических потерь. Следует отметить, что у карбюраторных ДВС доля насосных потерь при прикрытии дроссельной заслонки может достигать 35...50%. У дизельных двигателей, в которых поток воздуха, идущий в цилиндры, не регулируется, эта доля намного ниже. При наличии системы наддува величина момента сопротивления газов может быть отрицательной. В этом случае М rд является движущим моментом, а не моментом сопротивления. Однако за счет устройства, обеспечивающего наддув, соответственно возрастает указанный выше момент сопротивления механизмов (Ммд).
Таким образом, момент сопротивления двигателя складывается из 3-х моментов:
Мд = Мтд + Ммд Мгд. (2.22)
Значение Мд можно выразить через давление условных механических потерь (rд, МПа), т.е. среднее давление, которое должны развивать газы для равномерного проворачивания вала:
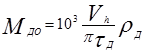
 (2.23)
(2.23)
где Vh - рабочий объем (литраж) двигателя, л;
tд - тактность двигателя.
Как показывает анализ, величина давления условных механических потерь практически не зависит от нагрузки (величины развиваемого момента) и прямо пропорциональна средней скорости движения поршней в цилиндрах (Сд, м/с):
rд » rдо + kдсп, (2.24)
где rдо - давление условных механических потерь при предельно малой угловой скорости вращения коленчатого вала, МПа;
kд - коэффициент, учитывающий возрастание механических потерь при увеличении средней скорости поршней, МПа с/м.
Значение средней скорости поршней Сп прямо пропорционально угловой скорости вращения коленчатого вала и длине хода:
сп = sпwе/p, (2.25)
где Sп – ход поршня, м;
wе – угловая скорость вращения коленчатого вала, рад/с.
Значения rдо и kд для различных типов двигателей приведены в табл. 2.1.
Таблица 2.1
Показатели механических потерь двигателей разных типов
| Тип двигателя | rдо, МПа | kд МПа с/м | Тип Двигателя | rдо, МПа | kд МПа с/м |
| С искровым зажиганием: а) Sп|Дп > 1 0,05 0,0155
б) Sп|Дп < 1 0,04 0,0135 | Дизели: а) раздельная камера сгорания 0,105 0,0138 б) нераздельная камера сгорания 0,105 0,0120 | ||||
2.4.2. Сопротивление дополнительного оборудования
При установке двигателя в подкапотное пространство к нему присоединяется вспомогательное (дополнительное) оборудование: вентилятор, воздухофильтр, генератор, компрессор, насос гидроусилителя руля, глушитель, коробка передач. В процессе работы двигателя указанное оборудование создает сопротивление, которое складывается из суммы соответствующих моментов:
Мо = Мфил + Мвен + Мглуш + Мген + Мкомп + Мнгур + Мкп. (2.26)
где Мфил; Мвен; Мглуш; Мген; Мкомп; Мнгур; Мкп. соответственно момент сопротивления, создаваемый воздухофильтром, вентилятором, глушителем, генератором, компрессором, насосом гидроусилителя рулевого привода, коробкой передач, Нм.
Количественное представление о влиянии вспомогательных агрегатов и механизмов грузового автомобиля на величину подкапотных потерь мощности дает табл. 2.2.
Как показывают исследования, при установке двигателя в подкапотное пространство наибольшие затраты мощности обусловливаются вентилятором системы охлаждения и насосом гидроусилителя руля суммарная доля которых составляет около 60%. При больших скоростях вращения коленчатого вала значительные потери создают глушитель, воздухофильтр и компрессор, на долю которых приходится в совокупности около 30% всех затрат мощности.
Таблица 2.2
Затраты мощности на привод вспомогательного (дополнительного) оборудования грузового автомобиля с карбюраторным двигателем
| N n/n
| Агрегаты и механизмы автомобиля
| Частота вращения коленчатого вала, об/мин | |||||
| 1000
| 2000
| 3000
| |||||
| кВт | % | кВт | % | кВт | % | ||
| · 1. | Воздухофильтр | 0 | 0 | 0,7 | 9,1 | 1,3 | 7,5 |
| · 3. | Вентилятор | 0,3 | 15,1 | 2,6 | 31,8 | 7,7 | 44,0 |
| · 3. | Глушитель | 0 | 0 | 1.0 | 12,7 | 2,6 | 14,7 |
| · 4. | Генератор | 0,1 | 5,7 | 0,2 | 2,7 | 0,3 | 1,8 |
| · 5. | Компрессор | 0,3 | 15,1 | 0,9 | 10,9 | 1,2 | 6,7 |
| · 6. | Насос гидроу-силителя руля | 0,9 | 45,3 | 2,4 | 21,8 | 2,6 | 14,7 |
| · 7. | Коробка передач | 0,4 | 18,9 | 0,9 | 10,9 | 1,8 | 10,6 |
| Итого: | 2,65 | 100 | 11,0 | 100 | 23,85 | 100 | |
Момент сопротивления вспомогательного оборудования можно вычислить исходя из той величины давления газов, которая обеспечивает его работу:
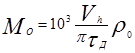 (2.27)
(2.27)
где rо - давление газов, обеспечивающее работу вспомогательного оборудования, МПа;
Значение rо зависит от частоты вращения вала и описывается квадратичной параболой
rо » rоо + kоwе2, (2.28)
где rоо - давление газов, необходимое для привода вспомогательного оборудования при минимальной скорости вращения коленчатого вала двигателя (0,010 МПа):
kо - коэффициент, учитывающий увеличение потерь на привод вспомогательного оборудования при увеличении угловой скорости вращения коленчатого вала (kо » 0,7 10-8 МПа с2; для дизелей с наддувом kо » 1,0 10-8 МПа с2).
В целом затраты на привод вспомогательного оборудования автомобиля достигают 12%...16% от максимального крутящего момента двигателя.
2.4.3. Сопротивление трансмиссии
В общем балансе сил сопротивления движению существенное значение имеет сопротивление трансмиссии. Ее источником является трение в зубчатых передачах, подшипниках валов, карданных шарнирах и шлицевых соединениях, а также перемешивание масла в картерах коробки передач (КП), раздаточной коробки (РК) и главной передачи (ГП).
Суммарные потери в трансмиссии можно представить в виде совокупности скоростных и силовых потерь. При этом момент силовых потерь (Мн) обусловлен силами трения при передаче нагрузки от двигателя к ведущим колесам автомобиля. В отличие от него момент, скоростных потерь (Мс), т.е. потерь холостого хода, обусловлен перемешиванием трансмиссионного масла. Таким образом, момент сопротивления трансмиссии, приведенный к ведущим колесам автомобиля, складывается из двух моментов:
Мтр = Мс + Мн. (2.29)
При передаче усилий к ведущим колесам потери в трансмиссии оцениваются коэффициентом полезного действия (см. формулу (1.19)):
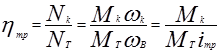 , (2.30)
, (2.30)
где Nт, Мт - мощность и момент, подводимые к трансмиссии;
iтр - передаточное отношение трансмиссии.
Учитывая (2.30), к.п.д. трансмиссии можно выразить формулой:
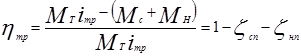 (2.31)
(2.31)
где 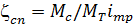 - коэффициент скоростных потерь;
- коэффициент скоростных потерь;
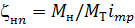 - коэффициент силовых потерь.
- коэффициент силовых потерь.
Как показывает анализ экспериментальных данных, величина силовых потерь в первом приближении прямо пропорциональна величине передаваемой ведущим колесам нагрузки (Мн ~ Mтiтр). Поэтому коэффициент силовых потерь (zнп) остается величиной постоянной. В отличие от силовых абсолютная величина скоростных потерь (Мс) от передаваемой нагрузки не зависит, а определяется скоростью движения автомобиля. Поэтому их доля (zсп) зависит от того, какова величина передаваемой нагрузки. При снижении нагрузки коэффициент скоростных потерь значительно возрастает. Это приводит к соответствующему снижению к.п.д. трансмиссии. Наоборот, увеличение передаваемого усилия вызывает снижение zсп, что приводит к повышению hтр. Переменный характер к.п.д. трансмиссии усложняет расчеты, поэтому в целях их упрощения значение hтр считают постоянным. Однако это не всегда оправдано и в некоторых случаях приводит к существенным погрешностям. Кроме того, следует иметь ввиду, что к.п.д. имеет пределы применимости.
В частности, при движении автомобиля накатом двигатель отключается от трансмиссии и Nт = 0. В этом случае показатель hтр теряет смысл. В силу указанных причин потери в трансмиссии целесообразно оценивать не относительной, а абсолютной величиной, т.е. не к.п.д., а приведенным к ведущим колесам моментом (Мтр) или силой (Ртр).
Как показывают экспериментальные исследования, значение момента сопротивления трансмиссии, приведенного к ведущим колесам автомобиля, можно представить в виде линейной функции от скорости движения (Vа) и передаваемого ведущим колесам момента (Мк):
Мтр = Мтро + mV а + mМк, (2.32)
где Мтро - момент сопротивления трансмиссии на холостом ходу при предельно малой скорости вращения валов. Нм;
m, m - коэффициенты, характеризующие скоростные и силовые потери в трансмиссии.
Значения Мтро, m и, m зависят от конструкции трансмиссии, N передачи и вязкости масла. При передаче усилий от ДВС к ведущим колесам автомобиля поток мощности проходит последовательно через несколько агрегатов и механизмов трансмиссии, в каждом из которых некоторая часть ее теряется вследствие сил сопротивления. При приведении последних к ведущим колесам важно знать, как сказывается момент сопротивления, создаваемый тем или иным агрегатом или механизмом (Мсk), на общем сопротивлении трансмиссии. Для этого рассмотрим процесс передачи усилий от ДВС к колесам.
Крутящий момент (Мk) и угловая скорость вращения (wk) на выходе из k-го агрегата трансмиссии являются одновременно входными величинами для последующего k+l агрегата.
Используя закон сохранения энергии, для каждого агрегата можно составить следующее уравнение:
Nk -1 = Nk + Nck, (2.33)
где Nk -1 , Nk , Nck, - соответственно мощность на входе, на выходе и
мощность, в самом агрегате.
Поделив правую и левую части уравнения (2.33) на угловую скорость вращения выходного вала k-ro агрегата (wк) и произведя перестановку членов, получим
Nk = Nk -1 ik - Nck, (2.34)
где ik = wk-1/wk - передаточное отношение k-ro агрегата.
Формула (2.34) справедлива как для отдельного агрегата (механизма), так и для всей трансмиссии в целом (если последняя рассматривается как система, состоящая из одного элемента).
Рассматривая трансмиссию автомобиля в целом как один элемент, на входе которого действует крутящий момент Мо, а на выходе момент Мп. можно составить аналогичное уравнение:
Mn = Moiтр –Мтр, (2.35)
где iтр = i1i2…ik…in - передаточное отношение трансмиссии.
Момент на выходе из трансмиссии является одновременно и моментом на выходе из последнего n-го агрегата. Поэтому, используя формулу (2.35), величину момента на выходе из трансмиссии (Мп) можно выразить через момент на выходе n-1 -агрегата (Mn-1):
Mn = Mn-1in – Mcn.
В свою очередь, Mn-1 можно выразить через момент на выходе из n-2 агрегата (Мn-2) и т.д. В конечном счете путем последовательных подстановок величину момента на выходе из трансмиссии можно выразить через момент на входе, а также передаточные отношения и моменты сопротивления составляющих трансмиссию агрегатов:
М n = (Mo – Mc1/i1 -…- Mck/i1i2…ik -…- Mcn/i1i2…in)iтр. (2.36)
k = 1, 2,…, n
Приравняв (2.35) и (2.36) и сделав соответствующие преобразования, получим момент сопротивления трансмиссии, приведенный к ведущим колесам автомобиля:
Mтр = Мci(i2…in) +…+ Mck(ik+1…in) +…+ Mcn. (3.37)
k = 1, 2, …, n
Из полученной формулы следует, что моменты сопротивления агрегатов трансмиссии могут складываться только с учетом передаточного отношения на участке трансмиссии от данного агрегата до ведущих колес. Другими словами, величина момента сопротивления, создаваемая k - м агрегатом, тем весомее в общем сопротивлении трансмиссии, чем "ближе" он расположен
к двигателю и "дальше" от ведущих колес.
Учитывая (2.37), величину силы сопротивления трансмиссии, состоящую, например, из основной коробки передач, раздаточной коробки и ведущих мостов, имеющих центральную передачу и колесные редукторы, можно представить в виде суммы сил сопротивления "соответствующих агрегатов:
Ртр = Ркп + Ррк + Рцр + Ркр, (2.38)
где Ркп, Ррк, Рцр, Ркр - силы сопротивления соответственно основной коробки передач, раздаточной коробки, центрального редуктора главной передачи и колесных редукторов, приведенные к ведущим колесам автомобиля.
Силы сопротивления указанных агрегатов и механизмов определяются по формулам:
- основной коробки передач:
Ркп = Мскпiркiцрiкр/rд, (2.39)
- раздаточной коробки:
Ррк = Мсркiцрiкр/rд, (2.40)
- центрального редуктора главной передачи:
Рцр = Мсцрiкр/rд, (2.41)
- колесных редукторов;
Ркр = Мскр/rд, (2.42)
где iрк, iцр, iкр - передаточные отношения соответственно раздаточной коробки, центрального редуктора главной передачи и колесных редукторов.
Учитывая, что суммарный момент сопротивления трансмиссии зависит от скорости движения и передаваемого усилия (формула 2.32), величину суммарной силы сопротивления можно выразить аналогичной функцией:
Ртр = Ртро + kVа + u Рт, (2.43)
где Ртро - сила сопротивления холостого хода трансмиссии при медленном проворачивании валов;
k и u - коэффициенты скоростных и силовых потерь;
Рт - сила тяги. создаваемая на ведущих колесах автомобиля за счет подвода к ним крутящего момента (Мк).
В формуле (2.43) второе слагаемое (kVа) характеризует величину дополнительной силы сопротивления, приведенной к ведущим колесам автомобиля, обусловленной скоростными потерями, а последнее слагаемое передачей усилий к ведущим колесам.
Зимой, пока агрегаты и механизмы трансмиссии еще не прогрелись, сопротивление трансмиссии может быть основным фактором сопротивления движению. Особенно велико сопротивление трансмиссии в момент трогания автомобиля с места, когда при низких температурах трансмиссионное масло теряет свою подвижность. Наблюдения показывают, что при температурах минус 40°С и ниже вязкость некоторых трансмиссионных масел может быть столь высока. что автомобиль из-за большого сопротивления даже не в состоянии самостоятельно тронуться с места.
2.5. Продольные усилия ведущих колес
При подводе крутящего момента к ведущим колесам возникают продольные реакции Rх, толкающие корпус автомобиля:
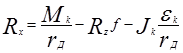 (2.44)
(2.44)
Из формулы (2.44) следует, что величина продольных усилий, создаваемых ведущими колесами, определяется, прежде всего, величиной подводимого к ним крутящего момента. Используя схему передачи усилий (рис. 2.7), определим величину указанного момента.
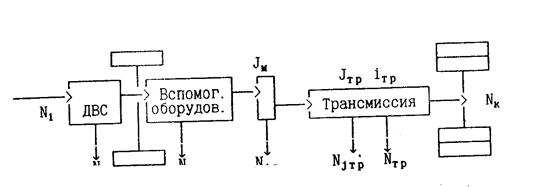
Рис.2.7. Передача мощности к ведущим колесам автомобиля
Для этого составим уравнение мощностного баланса:
Ni = Nд + Nо + Njд + Njтр + Nтр + Nк, (2.45)
где Ni - индикаторная мощность двигателя;
Nд - мощность условных механических потерь в двигателе;
Nо - мощность, затрачиваемая на привод вспомогательного оборудования;
Njд - мощность, затрачиваемая на разгон инерционных масс двигателя (маховика и соединенных с ним элементов);
Njтр - мощность, затрачиваемая на разгон инерционных масс трансмиссии (валов, шестерен,...);
Nтр - мощность, теряемая в трансмиссии;
Nк - мощность, подводимая к ведущим колесам.
Из (2.45) следует, что к ведущим колесам автомобиля подводится лишь часть индикаторной мощности ДВС, т.к. другая часть их теряется вследствие внутренних сопротивлений и разгона инерционных масс двигателя и трансмиссии.
Мощности, затрачиваемые на разгон инерционных масс двигателя и трансмиссии, определяются соответственно по формулам:
Njд = Jд(dwе/dt)wе; (2.46)
Njтр = Jтр(dwк/dt)wк, (2.47)
где Jд, Jтр - осевые моменты инерции вращающихся масс соответственно двигателя и трансмиссии, кгм2;
wе, wк - угловые скорости вращения соответственно колен. вала двигателя и ведущих колес автомобиля, рад/с.
Поделив правую и левую части уравнения (2.45) на угловую скорость вращения колес, получим уравнение моментов, которое можно привести к следующему виду:
Мк = Nк/wк = [М i – Мд – Мо – Jд(dwк/dt)iтр]iтр – Мтр – Jтр(dwк/dt). (2.48)
Подставив (2.48) в формулу (2.44), получим:
Rx = (M1/rд)iтр - (Mд/rд)iтр -(Mо/rд)iтр -(Mтр/rд) –
- Rzfc – (Jдiтр + Jтр + Jк)(dwк/dt)/rд. (2.49)
Формулу (2.49) можно представить следующим образом:
Rx = Р i – Pд – Po - Pтр – Р f – Pjк, (2.50)
где Р i = (М i / rд)iтр - индикаторная сила тяги автомобиля;
Рд = (Мд/rд)iтр - сила сопротивления двигателя;
Ро = (Мо/rд)iтр - сила сопротивления вспомогательного оборудования;
Ртр = (Мтр/rд) - сила сопротивления трансмиссии;
Р j к = (Jдiтр + Jтр + Jк)(dwе/dt)/rд - сила инерции вращающихся масс двигателя, трансмиссии и ведущих колес, приведенная к ведущим колесам автомобиля.
Разница между индикаторной силой тяги и силами, обусловленными внутренними сопротивлениями (Рд, Ро и Ртр), называется силой тяги автомобиля:
Рт = Р i – Рд – Ро – Ртр. (2.51)
Из (2.50) и (2.51) следует, что суммарное продольное усилие, прикладываемое в пятне контакта ведущих колес, равно силе тяги за вычетом сил сопротивления качения и инерции всех вращающихся масс автомобиля, связанных с ведущими колесами:
Rx = Рт – Р f – Р jк. (2.52)
Формула (2.52) означает, что суммарное продольное усилие на ведущих колесах автомобиля всегда меньше силы тяги на величину сил сопротивления качения и инерции.
2.6. Уравнение силового баланса
Уравнение силового баланса - это уравнение, выражающее равенство продольных сил, движущих автомобиль и оказывающих сопротивление его движению. При выводе уравнения силового баланса будем исходить из схемы сил, действующих на автомобиль при его движении (рис. 2.8).
| Рис.2.8. Силы и моменты при прямолинейном движении автомобиля |
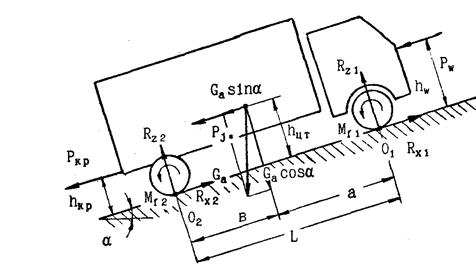
Складывая продольные силы с учетом направления их действия, получим следующее уравнение:
Rx2 = Rx1 + Pa - Pw – Pj* - P кр = 0. (2.53)
Подставим в данное уравнение вместо продольных реакций Rх2 и Rх1 полученные ранее выражения:
(Р1 – Рд – Ро – Ртр - Рe2 – Р f2) +
+ (-Рe1 – Р f1) - Pa - Pw – Pj* - Pкр = 0. (2.54)
Складывая силы сопротивления качения, испытываемые передними и задними колесами (Р f1, и Pf2). а также силы инерции (Pe2, Pe1 и Pj*), соответственно получим:
- суммарную силу сопротивления качению:
Р f1 + Pf2 = Pf (*)
- суммарную (приведенную) силу инерции автомобиля:
Pe2 + Pe1 + Pj* = Pj, (**)
где Pj - суммарная (приведенная) сила инерции автомобиля;
Pj* - сила инерции поступательного движения.
Используя (*) и (**), уравнение (2.54) можно привести к следующему виду:
Р1 = Рд – Ро + Рf + Pa + Pw + Pj + Pкр. (2.55)
Уравнение (2.55) представляет собой уравнение силового баланса. Оно выражает тот факт, что индикаторная сила тяги, развиваемая автомобилем, всегда уравновешивается алгебраической суммой всех сил сопротивления движению.
Если в левую часть уравнения (2.55) перенести силы сопротивления двигателя, вспомогательных механизмов и трансмиссии, то уравнение силового баланса можно представить в следующем виде:
Рт = Р f + Pa + Pw + Pj + Pкр. (2.56)
При движения автомобиля некоторые силы могут отсутствовать. Так, например, при равномерном движении нет силы сопротивления инерции (Р j = 0), при отсутствии прицепа - силы на крюке (Ркр = 0), а при отсутствии продольного уклона - силы сопротивления подъему (Pa = 0). При отключении двигателя от трансмиссии, например, при движении накатом или переключении передачи, отсутствует индикаторная сила тяги (Pi). Однако во всех случаях уравнения (2.55) и (2.56) сохраняют свою силу.
2.7. Приведенная сила инерции
Согласно (**) суммарная (приведенная) сила инерции автомобиля представляет собой сумму трех сил инерции:
Pj = Pj * + P e 2 + P e (2.57)
Подставим в формулу (3.57) соответствующие выражения входящих в нее сил. В результате получим следующую формулу:
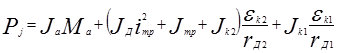 (***)
(***)
Выразим угловые ускорения колес через линейное ускорение автомобиля (eк2 = Ja / r к2; eк1 = Ja / r к1) после чего подставим их в формулу (***) и вынесем Ja и М a за скобки. В результате получим следующую формулу:
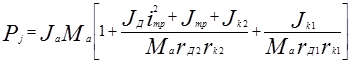 (2.58)
(2.58)
В формуле (2.58) выражение в квадратных скобках представляет собой безразмерную величину, которую называют коэффициентом учета вращающихся масс автомобиля. Обозначив указанный коэффициент буквой d, приведенную силу инерции автомобиля можно выразить формулой
Pj = JaMa d (2.59)
где d - коэффициент учета вращающихся масс автомобиля:
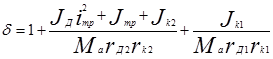 . (2.60)
. (2.60)
Из (2.60) следует, что d > 1. Это отражает тот факт. что часть массы автомобиля (маховик двигателя и все связанные с ним элементы, валы, шестерни, шарниры трансмиссии, а также колеса) испытывают инерции не только поступательного, но и вращательного движения.
Численные значения моментов инерции вращающихся масс различных марок и моделей автомобилей приведены в Приложении 2.
При отсутствии проскальзывания колес относительно опорной поверхности rк » rд » rст. Так как в таких случаях нет особой необходимости различать радиусы, то нижний индекс опускается. Поэтому формулу (3.60) можно представить так:
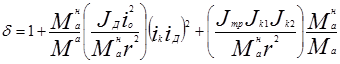

 (2.61)
(2.61)
где iк, iд, iо - передаточные отношения основной и дополнительной коробки передач (делителя, раздаточной коробки), а также главной передачи (центрального редуктора и колесных редукторов);
Ман - полная масса автомобиля при номинальной загрузке, кг.
Как показывает анализ, для всех одиночных автомобилей
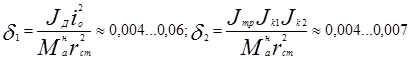
В целях удобства практического использования формулу (2.61) целесообразно представить в следующем виде:
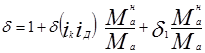 (2.62)
(2.62)
При отключении двигателя от трансмиссии (при накатах либо переключениях передач) инерция его вращения не влияет на режим движения автомобиля. Поэтому в целях соблюдения формальности значение момента инерции маховика следует принимать равным нулю (Jм = 0) или полагать, что d1 = 0.
2.8. Уравнение мощностного баланса
Умножив левую и правую части уравнения (2.55) на скорость движения, получим уравнение мощностного баланса автомобиля:
Ni = Nд + Nо + Nтр + Nf + Na + Nw + Nj + Nкр (2.63)
Так как разница между индикаторной мощностью N i и затратами мощности на преодоление внутренних сопротивления (Nд) есть так называемая эффективная мощность двигателя, то уравнение мощностного баланса можно представить и так:
Nе = Nо + Nтр + Nf + Na + Nw + Nj + Nкр (2.64)
Если в левую часть уравнения (2.64) перенести величину мощности, теряемой на привод вспомогательного оборудования (Nо) и в трансмиссии (Nтр), то получим еще одно уравнение мощностного баланса:
Nт = Nf + Na + Nw + Nj + Nкр (2.65)
где Nт - тяговая мощность автомобиля.
Тяговая мощность - это та часть индикаторной мощности двигателя, которая используется автомобилем для преодолевания внешних сопротивлений движению и ускорения.
Отношение тяговой мощности (Nт) к мощности, получаемой трансмиссией от силовой установкой автомобиля (Ni - Nд – Nо), представляет собой к. п. д. трансмиссии (hтр). Как отмечалось выше, значение hтр используется для оценки механических потерь, возникающих в трансмиссии.
2.9. Распределение усилий между ведущими колесами
При передаче усилий от двигателя к ведущим колесам в некоторых узлах трансмиссии автомобиля происходит разветвление потока мощности. К узлам деления мощности относится, прежде всего, раздаточные коробки и ведущие мосты. При этом в раздаточной коробке происходит деление потока мощности между ведущими мостами автомобиля, а в ведущем мосту - между колесами.
Функцию разделения потока мощности непосредственно выполняет дифференциал, который призван обеспечивать различные скорости вращения валов. Потребность в различных скоростях вращения колес возникает, прежде всего, при движении автомобиля на поворотах, когда путь проходимый левым и правым колесом, неодинаков. Соотношение кинематических параметров дифференциала выражается формулой
w1 + w2i = (1 + i)wд (2.66)
где w1, w2, wд - соответственно угловые скорости валов и корпуса самого дифференциала;
i - передаточное отношение дифференциала.
Передаточное отношение дифференциала численно равно отношению угловой скорости забегающего (т.е. более быстро вращающего) вала к угловой скорости отстающего вала при неподвижной коробке самого дифференциала.
Дифференциация скоростей вращения сопряжена с перераспределением мощности, а иногда и крутящего момента, между выходными валами дифференциала. Рассмотрим, от чего зависит распределение мощности и крутящих моментов между валами: Для этого составим уравнение силового и мощностного баланса дифференциала.
Из условия равновесия моментов сил, приложенных к дифференциалу, следует, что подводимый к дифференциалу крутящий момент (Мд) равен сумме крутящих моментов на его валах, т.е.
Мд = М1 + М2. (2.67)
При работе дифференциала часть подводимой к нему мощности (Nд) вследствие внутреннего трения теряется. Значение теряемой мощности можно выразить через момент сил внутреннего трения (Мтд) и разницу угловых скоростей вращения валов:
Nтд = 0,5Mтд(w2 - w1). (2.68)
Оставшаяся часть мощности (Nд - Nтд) распределяется между валами. Поэтому уравнение мощностного баланса можно выразить следующим образом:
Nд – Nтд = N1 + N2, (2.69)
где N1, N2 - мощности на валах дифференциала.
Решая совместно уравнения (2.66) - (2.69) и принимая, что (w1 < w2), получим формулы крутящих моментов на отстающем и забегающем валах:
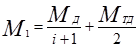 (2.70)
(2.70)
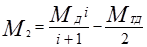 (2.71)
(2.71)
Как видно из формул (2.70) и (2.71), соотношение моментов на валах дифференциала определяется передаточным отношением и моментом внутреннего трения. Если передаточное отношение дифференциала равно единице (i = 1), то имеет место так называемый симметричный дифференциал, т. е. такой дифференциал, у которого при остановке коробки угловые скорости вращения валов по модулю одинаковы. Согласно (2.66) у симметричного дифференциала, имеющего i = i, всегда соблюдается соотношение
w1 + w2 = 2wд. (2.72)
Из формулы (2.72) вытекает, что при равенстве угловых скоростей валов их скорость всегда равна скорости вращения коробки дифференциала (w1 = w2 = wд), а всякое снижение скорости вращения одного вала на некоторую величину Dw (w1 = wд - Dw) вызывает автоматически приращение скорости вращения второго вала на точно такую же величину (w2 = wд + Dw).
По конструкции симметричные дифференциалы представляют собой, как правило, конические (гораздо реже цилиндрические) планетарные механизмы. Симметричный конический дифференциал - это самый распространенный тип дифференциала. Он устанавливается как в ведущих мостах автомобилей, так и раздаточных коробках. Для дифференциалов такого типа Мтд » 0, поэтому они всегда делят подводимый крутящий момент между его валами примерно поровну (М1 » М2). Действительно,
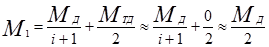
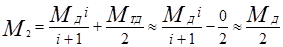
Если i > 1, то имеет место несимметричный дифференциал, который обеспечивает неодинаковые значения крутящих моментов на его валах. Если у такого дифференциала невелики и силы внутреннего трения (Мтд » 0), то указанное неравенство крутящих моментов на валах обеспечивается только за счет его кинематических свойств. При этом отношение моментов на его валах примерно прямо пропорционально передаточному отношению дифференциала, т.е. M2/M1 » 1. Необходимость в несимметричном дифференциале возникает, например, у 3-х осных автомобилей, у которых 1/3 крутящего момента необходимо подавать на передний ведущий мост, а 2/3 - на тележку из двух мостов. Указанное распределение обеспечивает дифференциал с передаточным отношением, равным двум (i = 2).
Использование в трансмиссии симметричных и несимметричных дифференциалов с низким внутренним трением имеет свои недостатки, главный из которых постоянное соотношение крутящих моментов, не позволяющее в полной мере использовать силы сцепления ведущих колес, находящихся в разных условиях. Это снижает суммарную силу тяги ведущих колес и отрицательно сказывается на проходимости автомобиля. Поэтому для повышения проходимости в раздаточной коробке, а иногда и в ведущих мостах, предусматривается установка блокируемых или самоблокирующихся дифференциалов. В некоторых случаях прибегают к бездифференциальному приводу ведущих мостов, при котором в раздаточной коробке отсутствует дифференциал, но предусматривается возможность отключения переднего моста.
У блокируемых и самоблокирующихся дифференциалов неравенство крутящих моментов обеспечивается, как правило, не за счет кинематических свойств, а за счет изменения сил внутреннего трения, которые препятствуют относительному вращению валов. Теоретическая возможность неравенства моментов вытекает из ранее полученных Формул (2.70) и (2.71). Поэтому для указанных видов дифференциалов важное значение имеет такой силовой показатель, как коэффициент блокировки, представляющий собой отношение момента сил внутреннего трения (Мтд) к подводимому моменту, т.е.
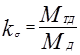 (2.73)
(2.73)
Если валы вращаются с разными скоростями (причем w1 < w2), то
работающий дифференциал, имея момент внутреннего трения Мтд, распределяет подводимый момент в пользу отстающего вала за счет забегающего:
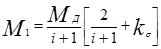 (2.74)
(2.74)
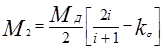
Как следует из формул (2.74), с увеличением коэффициента блокировки разница в моментах возрастает. У дифференциалов рассматриваемой группы коэффициент блокировки может изменяться от 0 до 1. При этом у самоблокирующихся дифференциалов значение ks изменяется в диапазоне от 0 до некоторого максимального значения, зависящего от типа конструкции (0,4...0,5 у дифференциалов кулачкового типа; 0,7...0,8 у дифференциалов червячного типа). У блокируемых дифференциалов ks » 0 либо ks = 1 (при блокировке). Заметим, что при полной блокировке дифференциала (ks = 1) угловые скорости валов равны и дифференциал теряет все свои кинематические свойства.
Таким образом, дифференциал обеспечивает не только разницу угловых скоростей валов, но и разницу в крутящих моментах.
Рассмотрим влияние сил внутреннего трения на к.п.д. дифференциала при его использования в ведущем мосту автомобиля.
Коэффициент полезного действия дифференциала можно представить в виде отношения мощности, отводимой от дифференциала (N1 + N2), к мощности, подводимой к нему (Nд):
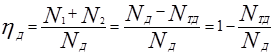
 (2.75)
(2.75)
Мощность, подводимую к дифференциалу, выразим через подводимый момент (Мд) и угловую скорость его коробки (wд): Nд = Мдwд.
Разницу угловых скоростей наружного (w2) и внутреннего (w1) колес при движении автомобиля со скоростью Vа, имеющего колею Нк, на повороте радиусом R можно выразить формулой
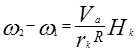 (2.76)
(2.76)
Угловая скорость вращения коробки дифференциала определяется формулой
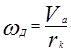 (2.77)
(2.77)
Подставляя (3.68), (3.76) и (3.77) в (3.75), после соответствующих сокращений получим
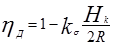 (2.78)
(2.78)
Из формулы следует, что к.п.д. межколесного дифференциала зависит не только от коэффициента блокировки, но и радиуса поворота. При прямолинейном движении hд » 1, а при движении на повороте значение hд меньше, но, несмотря на большое внутреннее сопротивление, коэффициент полезного действия не опускается ниже 0,88...0,90. Следовательно, большие внутренние сопротивления в самоблокирующихся дифференциалах не являются препятствием для их использования в ведущих мостах.
При выключении дифференциала из работы, т.е. его блокировании, внутренние потери близки к нулю, поэтому к.п.д. блокируемого дифференциала также близок к единице. Однако движение автомобиля при блокированном приводе сопровождается повышенным сопротивлением движений и циркуляцией паразитной мощности, обусловленной особенностями распределения усилий между ведущими колесами. Рассмотрим это явление на примере движения автомобиля с колесной формулой 4 х 4, у которого заблокирован дифференциал в раздаточной коробке.
У автомобилей такого типа передний и задний ведущие мосты имеют, как правило, одинаковые передаточные числа главной передачи. При заблокированном приводе ведущих мостов передние и задние колеса автомобиля вынуждены вращаться с одинаковой скоростью. Однако в реальности из-за разных траекторий движения путь, проходимый передними и задними колесами, неодинаков (особенно при поворотах), поэтому их угловая скорость должна быть разной. Более того, разная угловая скорость вращения колес необходима, зачастую даже при прямолинейном движении автомобиля.
Это связано с тем, что при одинаковой линейной скорости возможны
неодинаковые радиусы колес. Разница в радиусах передних и задних колес может быть обусловлена неодинаковым давлением воздуха в шинах, разной степенью износа протектора, разной вертикальной нагрузкой. Поэтому принудительное качение колес с одинаковой угловой скоростью сопряжено с возникновением дополнительных нагрузок в их приводе. Предположим, что радиус передних колес в силу тех или иных причин оказался больше, чем задних. Если колеса были бы абсолютно жесткими, то их качение неизбежно сопровождалось бы пробуксовкой передних, либо проскальзыванием задних. Однако колеса, снабженные эластичными шинами, за счет деформаций в тангенциальном направлении и соответствующего изменения радиусов качения способны перекатываться без пробуксовок и проскальзываний. Другими словами, кинематическая несогласованность вращения передних и задних колес компенсируется изменением кинематических радиусов их качения. Определим, каковы при этом крутящие моменты на передних и задних колесах.
Согласно (1.22), радиус качения при приложении к нему крутящего момента изменяется. Поэтому для передних и задних колес имеем:
rк1 = rко1 - lм1Mк1. (2.79)
rк2 = rко2 - lм2Mк2. (2.80)
При этом сумма крутящих моментов на ведущих колесах должна быть равна моменту всех сил сопротивления движению, приведенных к ведущим колесам (Мсд):
Мк1 + Мк2 = Мсд. (2.81)
Приравнивая (2.79) и (2.80) и учитывая (2.81), получим:
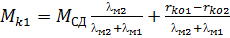 (2.82)
(2.82)
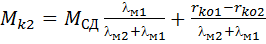 (2.83)
(2.83)
Из полученных формул следует, что при rко1 > rко2 крутящий момент на передних колесах будет больше, чем на задних, а при rко1 < rко2 - наоборот. При этом, если момент сил сопротивления движению (Мсд) невелик, а разница радиусов rко1 и rко2 значительна. то задние колеса могут перейти в ведомый (Мк2 = 0) или даже тормозной режим качения (Мк2 < 0). Последний случай особенно неблагоприятен, т.к. тормозной момент загружает не только силовой привод заднего моста, но и через раздаточную коробку передается в привод переднего, что обусловливает его дополнительную загрузку. В результате при блокировке дифференциала по ветви трансмиссии, передающей усилие к действительно ведущим колесам автомобиля, мощность передается от раздаточной коробки к колесам. В другой ветви, загруженной из-за отставания в скорости вращения тормозным моментом. усилие передается от дороги к колесам, а от них к раздаточной коробке, т.е. в противоположном направлении. Таким образом, обе ветви вместе с опорной поверхностью образуют замкнутый контур, внутри которого циркулирует мощность, которая загружает валы, но в итоге не приносит никакой пользы. Поэтому эту мощность называют "паразитной". Если кинематическое несоответствие достаточно велико, а сопротивление движению относительно мало, то паразитная мощность становится сопоставимой с мощностью, развиваемой автомобильным двигателем.
Циркуляция паразитной мощности возникает и при блокировке межколесного дифференциала. Поэтому при движении на дорогах с небольшим сопротивлением движению следует избегать блокировки привода, т.е. необходимо разблокировать дифференциал либо отключить передний ведущий мост.
Таким образом, при блокированном приводе распределение усилий между ведущими мостами отличается от дифференциального, при котором работающий дифференциал обеспечивает кинематическую согласованность вращения колес и разгружает тем самым трансмиссию.
2.10. Время и путь выбега
Время движения накатом (время выбега) определяется разницей между начальной и конечной скоростью движения, а также параметрами автомобиля и условиями движения. Формулу времени выбега можно получить в следующем виде:
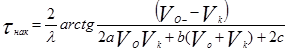
 (2.84)
(2.84)
где tнак - продолжительность движения накатом, с.
Путь, пройденный автомобилем за время наката, определяется по формуле
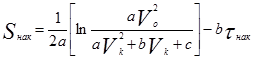 (2.85)
(2.85)
2.11. Динамический фактор автомобиля
Учитывая, что Ма =Ga/g и Рy = Gay), ускорение автомобиля можно выразить следующей формулой:
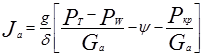 (2.86)
(2.86)
Из (2.86) следует, что ускорение, которое развивает автомобиль. Тем больше, чем больше отношение свободной силы тяги (Рсв = Рт – Рw) к полному весу автомобиля (Ga):
Показатель D представляет собой удельную свободную силу тяги. Его значение согласно (5.33) определяет интенсивность разгона автомобиля, т.е. его динамичность. По этой причине показатель D был назван Е.А. Чудаковым динамическим фактором автомобиля.
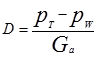 (2.87)
(2.87)
Используя динамический фактор, уравнение силового баланса можно представить так:
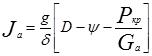
 (2.88)
(2.88)
Из уравнения (2.88) следует, что максимальное значение динамического фактора определяет:
а) максимальное ускорение, развиваемое автомобилем:
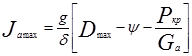 (2.89)
(2.89)
б) максимальное сопротивление дороги, преодолеваемое автомобилем:
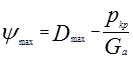 (2.90)
(2.90)
в) максимальное тяговое усилие на крюке:
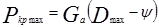 (2.91)
(2.91)
Таким образом, максимальное значение динамического фактора предопределяет предельные тяговые и скоростные показатели автомобиля.
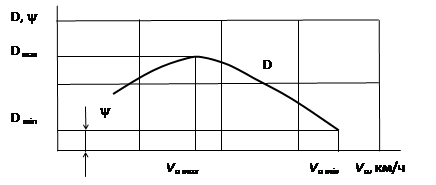
Представление о тягово-скоростных свойствах автомобилей дает его динамическая характеристика которая представляет собой зависимость динамического фактора от скорости автомобиля.
Как видно из графиков D = f(V), они представляют собой вогнутые кривые. На рис. 2.9 приведена динамическая характеристика автомобиля с гидромеханической трансмиссией. По мере увеличения скорости динамический фактор снижается. Отсутствие у кривых D = f(V) точек перегиба и резкое возрастание D при малых скоростях движения свидетельствует о лучшей, по сравнению с автомобилями с механической ступенчатой трансмиссией, способностью преодолевать возрастание внешней нагрузки, особенно при малых скоростях движения.
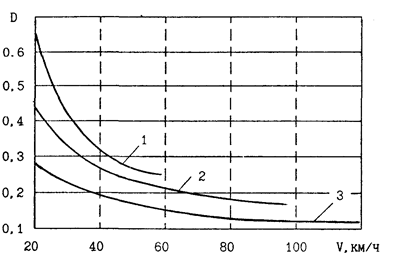
Рис.2.9. Динамическая характеристика автомобиля с гидромеханической трансмиссией
3. МЕТОДИКА РАСЧЕТА КОНСТРУКТИВНЫХ И ТЯГОВО-ЭКОНОМИЧЕСКИХ ПОКАЗАТЕЛЕЙ РАБОТЫ АВТОМОБИЛЯ
3.1. Определение полного веса автомобиля
При проектировании легкового автомобиля задается его сухой вес, определяющий его класс. Снаряженный вес берется на 10% больше сухого. Вес человека принимают равным 785,8 Н (масса 75 кг). Вес багажа, приходящегося на одного человека, включая водителя, принимается равным 98 Н.
Следовательно, полный вес, G, Н легкового автомобиля равен:
Ga=1,1k+883,8 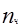 ,(3.1)
,(3.1)
где 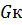 – сухой вес автомобиля;
– сухой вес автомобиля;
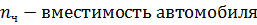 .
.
Вместимость автомобиля особо малого класса составляет 4 человека, малого и среднего – 5 человек, большого – 7 человек.
Для проектирования автобуса задается его тип и габаритная длина А, м. Снаряженный вес GСН, Н автобуса находят по коэффициенту собственного веса Ко, Н/м:
Gсн = Ко А. (3.2)
Коэффициент собственного веса определяют по обобщенным данным (Приложение 3).
Для городских сочлененных автобусов длинной А=16…18 м, КО = 7,5…8,0 кН/м. для междугородных автобусов и автобусов дальнего следования длинной 11…12 м КО = 10,0 кН/м.
Для определения полного веса автобуса необходимо знать вес груза (массу людей), погруженного в автобус.
Для городских не сочлененных и сочлененных автобусов при номинальной вместимости вес груза, Н. определяется из выражения
Gг = (1,85…2,15) А∙В (3.3)
Их нагрузка, Н, при предельной вместимости
Gг = (2,6…2,9) А∙В (3.4)
Для междугородных автобусов и автобусов дальнего следования нагрузка, Н, задается количеством посадочных мест и остается постоянной:
Gг = 1,5 А∙В, (3.5)
где А – габаритная длина, м; В – габаритная ширина, м.
Полный вес, Н, автобуса Gа = Gсн + Gг. (3.6)
При проектировании грузовых автомобилей снаряженную массу, Н, находят по грузоподъемности Gг и коэффициенту снаряженной массы К′о (Пприложение 4).
G сн = К′о Gг. (3.7)
Полный вес, Н, грузового автомобиля
G а = Gсн + Gг + G ч 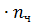 , (3.8)
, (3.8)
где G ч – вес одного человека (785,8 Н); 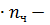 число человек в кабине (при Gг менее 50 кН
число человек в кабине (при Gг менее 50 кН 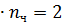 ; при Gг более или равным 50 кН
; при Gг более или равным 50 кН 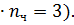
3.2. Определение размера шин
Размер шины выбирают по нагрузке, приходящейся на шину, и заданному внутреннему давлению в шине. Для шин грузовых автомобилей используют ГОСТ 17393-72 и ГОСТ 5513-75. Для шин легковых автомобилей ГОСТ 20993-75 и ГОСТ 4754-80. Справочный материал по шинам автомобилей приведен в Приложении 5, а временные нормы эксплуатационного пробега шинавтотранспортных средств в Приложении 6. Данные приложения позволяют определять марку шин на каждый автомобиль любой категории, а следовательно, наружный диаметр D, 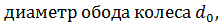 статический радиус r с а по нему радиус качения колеса r к. Для диагональных шин грузовых автомобилей r к = 1,02 r с, для радиальных r к = 1,04 r с .
статический радиус r с а по нему радиус качения колеса r к. Для диагональных шин грузовых автомобилей r к = 1,02 r с, для радиальных r к = 1,04 r с .
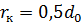 +(1 - lш)bш,
+(1 - lш)bш,
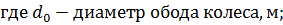
lш – коэффициент радикальной деформации шины;
bш – высота профиля шины в свободном состоянии, м.
Давление в шинах зависит от типа автомобиля – легковой, грузовой, относится ли он группе Б (для движения на всех дорогах) или к группе А (для движения на дорогах I и II категорий). Давление колеблется от 0,75 Мпа до 0,15 Мпа.
3.3. Расчет требуемой мощности автомобильного двигателя
Мощность автомобильного двигателя, кВт, для движения полностью нагруженного автомобиля с заданной максимальной скоростью
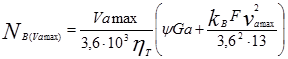 , (3.9)
, (3.9)
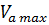 – при заданных дорожных условиях, км/ч;
– при заданных дорожных условиях, км/ч;
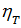 – механический к.п.д. трансмиссии при движении с максимальной скоростью. Для легкового автомобиля и автомобилей ограниченной грузоподъемности
– механический к.п.д. трансмиссии при движении с максимальной скоростью. Для легкового автомобиля и автомобилей ограниченной грузоподъемности 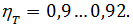 Для полноприводных
Для полноприводных 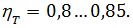 Для тяжелых грузовых
Для тяжелых грузовых 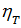 = 0,85…0,88;
= 0,85…0,88;
y - приведенный коэффициент дорожного сопротивления, при движении по горизонтальному ровному участку дороги y=f (f – коэффициент сопротивления качению, Приложение 7). При движении в гору y = f+i, под гору y = f - i. Здесь i = tgaд, а aд – угол уклона дороги;
Кв – коэффициент сопротивления воздуха (обтекаемости), Н∙с2/м4 (выбираем по типу автомобиля из Приложения 1);
F – лобовая площадь автомобиля, м2, приближенно определяется по формулам:
для легковых автомобилей F = 0,78 ВаНа; (3.10)
для грузовых автомобилей F = ВНа, (3.11)
где На – наибольшая высота автомобиля, м;
Ва – наибольшая ширина легкового автомобиля, м;
В – ширина колеи грузового автомобиля, м.
Для более лучших динамических качеств автомобилей при движении со средними эксплуатационными скоростями необходимо, чтобы максимальная мощность двигателя, кВт, была в пределах:
карбюраторного Ne max = (1,05…1,1) Ne (Va max), (3.12)
дизеля Ne max = Ne ном. (3.13)
Величину мощности, кВт, определяют расчетным путем по формуле Лейдермана:
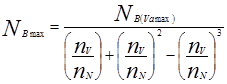 , (3.14)
, (3.14)
где nV – частота вращения коленчатого вала при максимальной скорости движения, мин-1; nN – частота вращения коленчатого вала в режиме максимальной мощности, мин-1.
У карбюраторных двигателей грузовых автомобилей 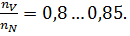 Для дизелей
Для дизелей 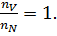
Для современных карбюраторных двигателей грузовых автомобилей 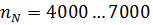 мин-1, для дизелей
мин-1, для дизелей 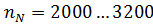 мин-1. Меньшие частоты вращения относятся к двигателям большого литража.
мин-1. Меньшие частоты вращения относятся к двигателям большого литража.
3.4. Расчет и построение внешней скоростной характеристики двигателя
Внешнюю скоростную характеристику двигателя строят для интервала частот вращения коленчатого вала:
- для карбюраторных двигателей от n е min = 600…800 мин-1 до n е max = (1,05…1,2) n е ном мин-1.
- для дизелей от n е min = 800…1000 мин-1 до n е ном мин-1.
Затем определяют промежуточные точки частот вращения.
Для дизелей:
- эффективная мощность, кВт,
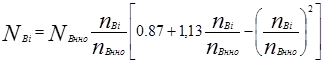
- эффективный крутящий момент, Н∙м,
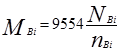
- удельный расход топлива, г/кВт∙ч,
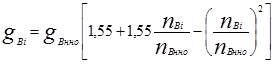
- часовой расход топлива, кг/ч,
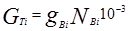
Для карбюраторных двигателей:
- эффективная мощность, кВт,
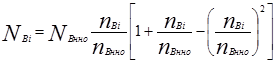
- эффективный крутящий момент, Н∙м,
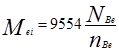
- удельный расход топлива, г/кВт∙ч,
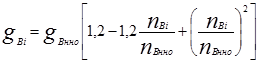
- часовой расход топлива, кг/ч,
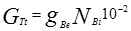
где i – текущее значение показателя;
nei – задают от величины ne min, с интервалом 200 мин-1.
Соответствующие расчеты сводят в таблицу 3.1.
Таблица 3.1 – Расчетные показатели работы двигателя
| Расчетные точки | Показатели работы двигателя | ||||
| nei, мин-1 | Nei, кВт | Mei, Н∙м | gei, г/кВт∙ч | GTi, кг/ч | |
| 1 | 800 | «…» | «…» | «…» | «…» |
| 2 | 1000 | «…» | «…» | «…» | «…» |
| … | … | «…» | «…» | «…» | «…» |
| i | 2500 | «…» | «…» | «…» | «…» |
На основании расчетных показателей строят внешнюю скоростную характеристику двигателя в зависимости от частоты вращения коленчатого вала (nei) (см. рисунок 3.1).
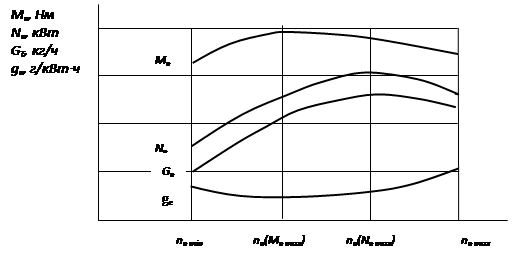 |
Рисунок 3.1 – Внешняя скоростная характеристика карбюраторного двигателя
3.5. Расчет передаточных чисел агрегатов трансмиссии
Расчет будет осуществляться (в учебных целях) только для прямой передачи, т. е. для передачи, у которой передаточное число коробки передач равно единице. При движении на прямой передаче передаточное число коробки передач iк =1, скорость движения равна максимальной Va max. Рассчитываем передаточное число главной передачи
io =0,377 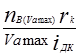 , (3.22)
, (3.22)
где 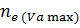 – частота вращения коленчатого вала двигателя при максимальной скорости движения на прямой передаче;
– частота вращения коленчатого вала двигателя при максимальной скорости движения на прямой передаче;
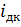 – передаточное число на высшей передаче в дополнительной коробке передач.
– передаточное число на высшей передаче в дополнительной коробке передач.
3.6. Расчет и построение динамической характеристики автомобиля
Динамическая характеристика автомобиля представляет собой зависимость динамического фактора от скорости движения автомобиля на различных передачах в трансмиссии при полной нагрузке. Для расчета скоростей движения автомобиля выбирают расчетные точки изменения частоты вращения коленчатого вала двигателя nei:
- для карбюраторных двигателей от ne min до ne max;
- для дизелей от ne min до ne ном.
Количество расчетных точек i по частотам вращения коленчатого вала двигателя следует выбирать из следующих условий:
- для карбюраторных двигателей: первая точка соответствует частоте вращения коленчатого вала ne min; вторая выбирается в середине интервала от ne min до ne (Ме mах); третья - при ne (Ме mах); четвертая - от ne (Ме mах) до ne (Nе mах); пятая – при ne (Nе mах); шестая – в середине интервала от ne (Nе mах) до ne max; седьмая – при ne max.
- для дизелей: первая точка соответствует частоте вращения коленчатого вала ne min; вторая выбирается в середине интервала от ne min до ne (Ме mах); третья - при ne (Ме mах); четвертая – в середине интервала от ne (Ме mах) до ne max; пятая – при ne max.
Затем подсчитывают величину скоростей, км/ч, для прямой передачи 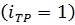 , в каждой выбранной точке частоты вращения коленчатого вала двигателя по формуле (22)
, в каждой выбранной точке частоты вращения коленчатого вала двигателя по формуле (22)
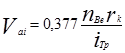

 . (3.23)
. (3.23)
Рассчитанные данные сводят в таблицу 3.2.
Таблица 3.2 - Исходные данные для построения динамической характеристики на прямой передаче
| nei, мин-1 | 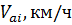
| 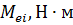
| 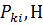
| 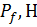
| 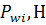
| 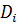
|
| ne min | … | … | … | … | … | … |
| … | … | … | … | … | … | … |
| ne max | … | … | … | … | … | … |
Далее, с учетом выбранных расчетных точек nie определяют:
- величину касательной силы тяги, Н, для прямой передачи
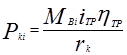
где 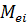 – величины крутящих моментов (рассчитываются методом интерполяции для выбранных расчетных точек nie из таблицы 3.1);
– величины крутящих моментов (рассчитываются методом интерполяции для выбранных расчетных точек nie из таблицы 3.1);
- величину силы, Н, сопротивления качению в зависимости от скорости
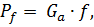 (3.25)
(3.25)
где 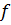 – коэффициент сопротивления качению в зависимости от скорости.
– коэффициент сопротивления качению в зависимости от скорости.
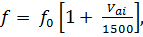 (3.26)
(3.26)
здесь 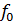 – коэффициент сопротивления качению при движении с малой скоростью (Приложение 7);
– коэффициент сопротивления качению при движении с малой скоростью (Приложение 7);
- величину силы сопротивления воздуха, Н, для прямой передачи
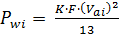 , (3.27)
, (3.27)
где величины 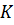 (коэффициент лобового сопротивления) и
(коэффициент лобового сопротивления) и 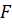 (площадь миделева сечения) находят в зависимости от марки автомобиля (Приложение 1);
(площадь миделева сечения) находят в зависимости от марки автомобиля (Приложение 1);
величину динамического фактора для прямой передачи
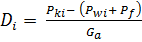 . (3.28)
. (3.28)
 Расчетные значения величин
Расчетные значения величин  также заносят в таблицу 3.2.
также заносят в таблицу 3.2.
 | |||
 | |||
Рисунок 3.2 – Динамическая характеристика автомобиля на прямой передаче
3.7. Расчет и построение экономической характеристики автомобиля
Экономическая характеристика автомобиля показывает расход топлива из учета 100 км пробега в зависимости от скорости движения и дорожного сопротивления, при равномерном и прямолинейном движении на прямой передаче.
По выбранным расчетным точкам частот вращения nei (таблица 3.2) и соответствующим скоростям движения vi для прямой передачи определяется мощность двигателя, кВт, требуемая для движения автомобиля на одной из заданных дорог до полной загрузки дигателя:
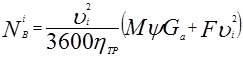 . (3.28)
. (3.28)
Удельный расход топлива 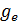 является величиной, зависящей от нагрузочного режима работы двигателя. По отношениям мощностей, соответствующих внешней скоростной характеристике двигателя и рассчитанных
является величиной, зависящей от нагрузочного режима работы двигателя. По отношениям мощностей, соответствующих внешней скоростной характеристике двигателя и рассчитанных
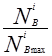
определяют величину коэффициента К N по графику (рис 3.3), а далее делают проверочный расчет по следующим формулам:
К N = 1,97124 – 2,53537 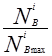 +1,5506
+1,5506 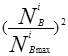 + 0,0031123
+ 0,0031123 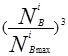 (3.29) -для дизелей;
(3.29) -для дизелей;
К N = 2,588 – 3,084 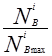 +0,925(
+0,925( 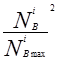 ) + 0,558(
) + 0,558( 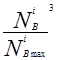 ) (3.30) - для карбюраторных двигателей.
) (3.30) - для карбюраторных двигателей.
Значения 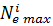 подсчитывают по формуле (3.28), а значения
подсчитывают по формуле (3.28), а значения 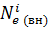 берут из таблицы 3.1, внешней скоростной характеристики двигателя.
берут из таблицы 3.1, внешней скоростной характеристики двигателя.
 |
Рисунок 3.3 – Зависимости коэффициента К N
Удельный расход топлива 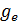 также является величиной, зависящей и от скоростного режима работы двигателя. По отношениям мощностей, соответствующих внешней скоростной характеристике двигателя и рассчитанных
также является величиной, зависящей и от скоростного режима работы двигателя. По отношениям мощностей, соответствующих внешней скоростной характеристике двигателя и рассчитанных 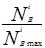 находят коэффициент КП по графику (рис. 3.4) по графику (рис 3.3), а далее делают проверочный расчет по следующим формулам:
находят коэффициент КП по графику (рис. 3.4) по графику (рис 3.3), а далее делают проверочный расчет по следующим формулам:
КП = 1,2177 – 0,580437 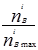 +0,91829(
+0,91829( 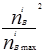 )+ 0,271465
)+ 0,271465 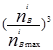 (3.31)
(3.31)
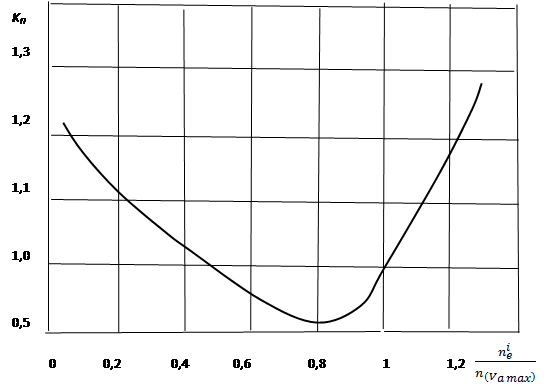
Рисунок 3.4 – Зависимости коэффициента КП
По формуле 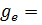 КП К N
КП К N 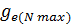 подссчитывается удельный расход топлива для разных скоростей движения автомобиля.
подссчитывается удельный расход топлива для разных скоростей движения автомобиля.
Согласно полученным для 
 на прямой передаче определяют удельный путевой расход топлива:
на прямой передаче определяют удельный путевой расход топлива:
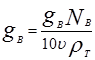 ,(3.32)
,(3.32)
где rТ - плотность для бензина rТ = 0,725 кг/л, для дизельного топлива rТ = 0,825 кг/л.
По формуле (3.32) аналогично проводится расчет расхода топлива на 100 км пробега автомобиля Qs.
Далее производится построение экономической характеристики автомобиля для заданных дорожных условий, график которой показан на рис. 3.5
3.8. Расчет и построение мощностного баланса автомобиля
Уравнение мощностного баланса автомобиля, кВт, в общем случае имеет вид:
NT = Ne hTp = Ny ± Nj + Nw, (3.33)
где NT – мощность, кВТ, подводимая к ведущим колесам:
NT = 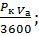 (3.34)
(3.34)
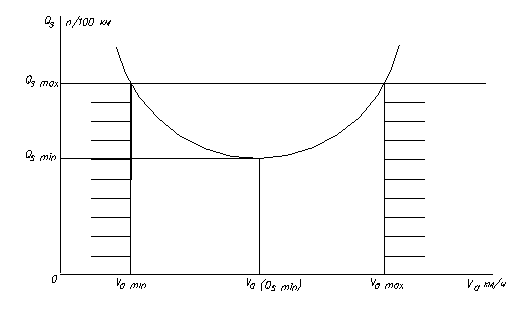
Рисунок 3.5 – Экономическая харатеристика автомобиля
здесь Рк -0 касательная сила тяги, Н;
Ny - мощность, кВт, затрачиваемая на преодоление дорожных сопротивлений: Ny = 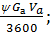 (3.35)
(3.35)
Nj – мощность, кВт, затрачиваемая на разгон автомобиля:
Nj = 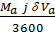 ; (3.36)
; (3.36)
Nw – мощность, затрачиваемая на преодоление сопротивления воздуха:
Nw = 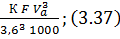
Построение графика мощностного баланса выполняют только для случая равномерного движения (Nj=0, j = 0) автомобиля по горизонтальной дороге (a=0) на прямой передаче.
Расчетные данные сводят в таблицу вида 3.3.
Таблица 3.3 – Исходные данные для построения мощностного баланса автомобиля.
| nei, об/мин | Vai, км/ч | Nei,кВт | NiT, кВт | Niy, кВт | Niw, кВт | Niy+ Niw, кВт |
| n1e | ||||||
| … | ||||||
| nme |
По данным таблицы строят график мощностного баланса автомобиля (рис. 3.5).
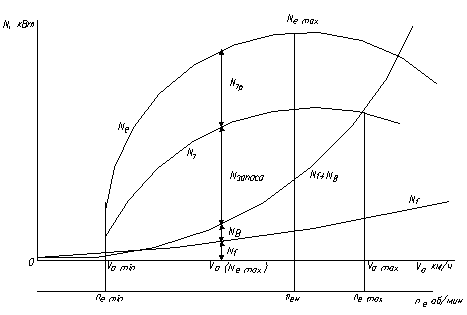
Рисунок 3.5 – График мощностного баланса автомобиля








