Методические рекомендации по оформлению и выполнению контрольной работы
Контрольная работа представляет собой работу практического характера. Подготовка контрольной работы предполагает владение навыками практической работы: умение анализировать задание и формулировать подходы к его решению; подбирать литературу и работать с ней, умение добиться практического результата с помощью стандартного набора средств.
Вариант контрольной работы = списочному номеру в группе (уточняйте у преподавателя). При выполнении контрольной работы надо строго придерживаться следующих правил:
ü На листе должны быть ясно написаны фамилия обучающегося, его инициалы, группа, название темы;
ü В работу должны быть включены все задачи, указанные в задании, строго по своему варианту.
ü Решение задач надо располагать в порядке, указанном в заданиях, сохраняя номера задач. Задачи выполняются строго по порядку номеров, записывается полное условие каждого номера, аккуратно и подробно оформляется решение (с пояснениями), формулируется четкий ответ.
ü Перед решением каждой задачи надо выписать полностью её условие. Если несколько задач имеют общую формулировку, следует, переписывая условие задачи, заменить общие данные конкретными из соответствующего номера.
Теоретические основы темы
1. Основные сведения из теории
1.1Арксинус числа
Определение: Арксинусом числа а℮[-1;1] называется такое число α℮[- 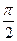 ;
; 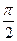 ], синус которого равен а.
], синус которого равен а.
Обозначение: arcsina , - 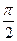 ≤ arcsina ≤
≤ arcsina ≤ 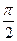
Определение: arcsina = α ↔ sinα = а
| а | 0 | 
|  ( ( 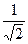 ) )
| 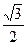
| 1 |
| arcsina | 0 | 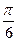
| 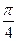
| 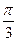
| 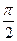
|
Свойства: 1) sin(arcsina)=а
2) arcsin(sinα)=α
3) arcsin(-a)=- arcsina
Таблица значений arcsina
| а | - 
| -  (- (- 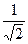 ) )
| - 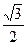
| -1 |
| arcsina | - 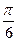
| - 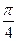
| - 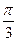
| - 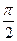
|
1. 2. Арккосинус числа
Определение: Арккосинусом числа а℮[-1;1] называется такое число α℮[0;π], косинус которого равен а.
Обозначение: arccosa , 0≤ arccosa ≤ π
Определение: arccosa = α ↔ cosα = а
Свойства: 1) cos(arccosa)=а
2) arccos(cosα)=α
3) arccos(-a)=π- arccosa
Таблица значений arccosa
| а | 0 | 
|  ( ( 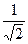 ) )
| 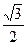
| 1 |
| arccosa | 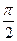
| 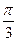
| 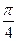
| 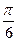
| 0 |
| а | - 
| -  (- (- 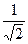 ) )
| - 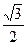
| -1 |
| arccosa | 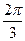
| 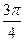
| 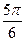
| π |
1. 3. Арктангенс числа
Определение: Арктангенсом числа а℮[- 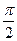 ;
; 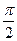 ] называется такое число α, тангенс которого равен а.
] называется такое число α, тангенс которого равен а.
Обозначение: arctga , - 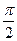 ≤ arccosa ≤
≤ arccosa ≤ 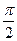
Определение: arctga = α ↔ tgα = а
Свойства: 1) tg(arctga)=а
2) arctg(tgα)=α
3) arctg(-a)=- arctga
Таблица значений arctga
| а | 0 | 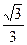
| 1 | 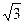
|
| arctga | 0 | 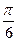
| 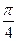
| 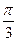
|
| а | - 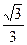
| -1 | - 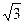
|
| arctga | 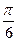
| 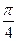
| 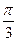
|
1.4. Уравнение sinx=a
 |
sinx=a
x=(-1)narcsina+ πn,n 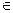 Z
Z
1.5. Уравнение cosx=a
 |
cosx=a
x=±arccosa+ 2πn,n 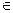 Z
Z
1.6. Уравнение tgx=a
 |
tgx=a
x=arctgx+ πn,n 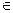 Z
Z
2. Примеры и упражнения
Пример: Найти значение выражения:
1) аrcsin1-arcsin(-1)+ arcsin(  )+arcsin(-
)+arcsin(- 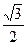 ) =
) =
= 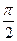 -(-
-(- 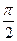 )+
)+ 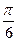 +(-
+(- 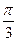 )=
)= 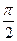 +
+ 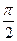 +
+ 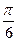 -
- 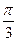 =
= 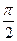 (3+
(3+ 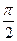 (3+
(3+ 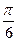 (1-
(1- 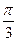 (2= =
(2= = 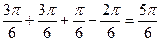
2) tg(2 arcsin  )=tg(2∙
)=tg(2∙ 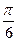 )=tg
)=tg 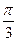 =
= 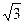
3) cos(аrcsin(tg 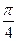 ))= cos(аrcsin1)= cos
))= cos(аrcsin1)= cos 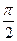 =0
=0
4) аrcsin(cos(аrcsin(  tg(
tg( 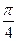 )))=аrcsin(cos(аrcsin(
)))=аrcsin(cos(аrcsin(  ∙1))= =аrcsin(cos(аrcsin
∙1))= =аrcsin(cos(аrcsin  ))= аrcsin(cos
))= аrcsin(cos 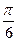 )= аrcsin
)= аrcsin 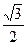 =
= 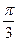
5) 2аrccos0+3arccos1=2∙ 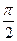 +3∙0=
+3∙0= 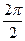 +0=π
+0=π
6) 12аrccos 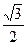 -3arccos(-
-3arccos(-  )=12∙
)=12∙ 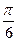 -3∙
-3∙ 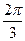 =2π-2π=0
=2π-2π=0
7) аrccos (- 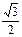 )+3аrcsin(-1)=
)+3аrcsin(-1)= 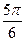 +3∙(-
+3∙(- 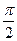 )=
)=
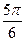 -
- 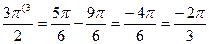
8) sin(6аrccos  )= sin(6∙
)= sin(6∙ 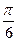 )= sinπ=0
)= sinπ=0
Пример 2: Решить тригонометрическое уравнение:
(1-2 sin х )(1-3 cos х )=0
Решение:
1-2sinх=0 или 1-3cosх=0
-2sinх=-1 - 3cosх=-1
sinх=  cos=-
cos=- 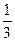
х1=(-1)narcsin  +πn,n℮Z х2=±arccos(-
+πn,n℮Z х2=±arccos(- 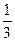 )+πn,n℮Z
)+πn,n℮Z
х1=(-1)n∙ 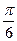 +πn,n℮Z х2=-arccos
+πn,n℮Z х2=-arccos 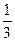 +πn,n℮Z
+πn,n℮Z
Ответ: х1=(-1)n∙ 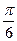 +πn,n℮Z х2=-arccos
+πn,n℮Z х2=-arccos 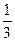 +πn,n℮Z
+πn,n℮Z
Пример 3: Решить тригонометрическое уравнение:
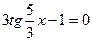 .
.
Решение:
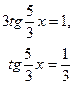 .
.
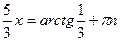 .
.
Разделим левую и правую части уравнения на 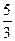 :
: 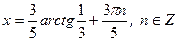 .
.
Ответ: 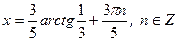
Пример 4: Решить тригонометрическое уравнение:
2 sin 2 х+ sin х-6=0
Решение:
Пусть sinх=t, t℮[-1;1]
2t²+t – 6 = 0
Решение:
а=2, b=1, с=-6
t1,2= 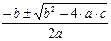 =
= 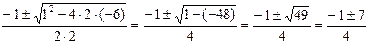
t1= 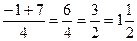 t2=
t2= 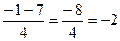
t1 = 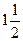
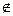 [-1;1],т.е. не уд. t2 = -2
[-1;1],т.е. не уд. t2 = -2 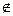 [-1;1],т.е. не уд.
[-1;1],т.е. не уд.
Ответ: решений нет
Пример 5: Решить тригонометрическое уравнение:
2 sin 2 х+5 cos х-5=0
Решение:
2(1-cos2х)+5cosх-5=0
2-2cos2х+5cosх-5=0
-2cos2х+5cosх-3=0 :(-1)
2cos2х-5cosх+3=0
Пусть cosх=t, t℮[-1;1]
2t²-5t +3 = 0
а=2, b=-5, с=3
t1,2= 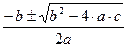 =
= 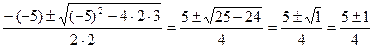
t1= 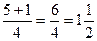 t2=
t2= 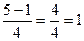
t1= 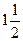 t2=1
t2=1
cosх= 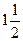
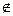 [-1;1],т.е. не уд. cosх=1(частный случай)
[-1;1],т.е. не уд. cosх=1(частный случай)
х=2πn,n℮Z
Ответ: х=2πn,n℮Z
Пример 6: Решить тригонометрическое уравнение:
4 sin 2 x -5 sinx ∙ cosx -6 cos 2 x =0
Решение:
4sin2x-5sinx∙cosx-6cos2x=0(разделим на то, что стоит перед знаком «=», т.е. на cos2х)
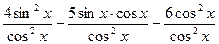 =0
=0
4tg2x-5tgx-6=0
Пусть tgx=t
4t2-5t-6=0
а=4, b=-5, с=-6
t1,2= 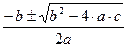 =
= 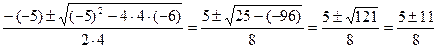
t1= 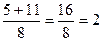 t2=
t2= 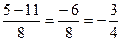
t1=2 t2=- 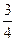
tgx=2 tgх=- 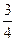
х1= arctg2+πn,n℮Z х2= arctg(- 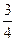 )+πn,n℮ Z,
)+πn,n℮ Z,
Ответ: х1= arctg2+πn,n℮Z, х2=-arctg 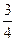 +πn,n℮Z
+πn,n℮Z
Варианты контрольной работы
Задание 1: Найти значение выражения
Вариант 1:
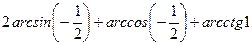
Вариант 2:
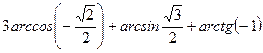
Вариант 3:
arcsin  +4 arcsin
+4 arcsin 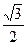 - arccos
- arccos  + аrctg
+ аrctg 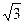
Вариант 4:
arcsin(сos(аrctg 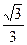 ))
))
Вариант 5:
аrctg 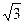 +аrccos
+аrccos 
Вариант 6:
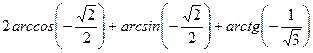
Вариант 7: 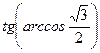
Вариант 8:
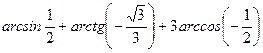
Вариант 9:
аrctg (сos(аrctg 1))
Вариант 10:
аrctg 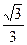 -12аrcsin(-
-12аrcsin(- 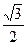 )
)
Вариант 11:
аrcsin(- 1) + аrccos (-1) +аrctg 0
Вариант 12:
cos(аrctg 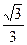 )
)
Вариант 13:
arctg1+ arccos 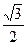 - arcsin
- arcsin  - аrctg
- аrctg 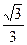
Вариант14:
аrctg(- 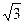 )+ аrccos(-
)+ аrccos(-  )-аrcsin(-
)-аrcsin(-  )
)
Вариант 15:
arcsin  +4 arcsin
+4 arcsin 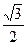 - arccos
- arccos  + аrctg
+ аrctg 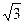
Вариант 16:
аrccos(-  )+ аrctg 1
)+ аrctg 1
Вариант 17:
аrcsin1 + аrccos 1 +аrctg 0
Вариант 18:
аrcsin0 + аrccos +аrctg 0
Вариант19:
аrctg 1+аrcsin 
Вариант 20 :
аrccos  + аrctg 1
+ аrctg 1
Вариант 21:
аrccos(-  )- аrctg(- 1)
)- аrctg(- 1)
Вариант 22:
аrctg (-1)-аrcsin(-  )
)
Вариант 23:
cos(аrctg 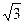 )
)
Вариант 24:
tg(аrcsin  )
)
Вариант 25:
tg(аrcsin 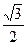 )
)
Вариант 26:
cos(аrctg 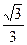 )
)
Вариант 27:
аrctg(- 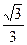 )- аrcsin(-
)- аrcsin(-  )+ аrccos (-
)+ аrccos (-  )
)
Вариант 28:
arcsin  +4 arcsin
+4 arcsin 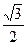 - arccos
- arccos  + аrctg
+ аrctg 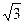
Вариант 29:
аrctg(- 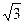 )+ аrccos(-
)+ аrccos(-  )-аrcsin(-
)-аrcsin(-  )
)
Вариант 30:
arctg1+ arccos 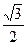 - arcsin
- arcsin  - аrctg
- аrctg 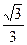
Задание 2: Решить тригонометрическое уравнение:
Вариант 1:
1) sinx= 
2) 3cos²x – 5cosx +2 =0
3) 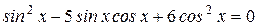
Вариант 2:
1) sinx= 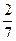
2) 4sin²x -11sinx +8 =0
3) 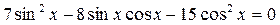
Вариант 3:
1) (2sinx+1)(2sinx- 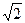 )=0
)=0
2) 8cos²x -12sinx +7 =0
3) 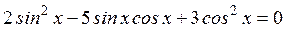
Вариант 4:
1) (sin7x+1)(4sinx-2)=0
2) 2sin²x +5cosx -5 =0
3) 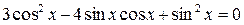
Вариант 5:
1) Sin5x=- 
2) sin²x -5sinx·cosx -6cos²x =0
3) 4cos²x – 4cosx -3 =0
Вариант 6:
1) Sin10x=- 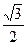
2) 3sin²x -5sinx·cosx +2cos²x =0
3) 4cos²x -13sinx +1 =0
Вариант 7:
1) tgx=0
2) 2sin²x -sinx·cosx -cos²x =0
3) (2sinx- 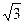 )(2sinx+1)=0
)(2sinx+1)=0
Вариант 8:
1) ( 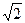 sinx+1)(2sinx-1)=0
sinx+1)(2sinx-1)=0
2) 4sin²x +4sinx -3 =0
3) sin²x -5sinx·cosx -6cos²x =0
Вариант 9:
1) Cosx= 
2) 2sin2x+sinx-1=0
3) 3sin2x-5sinx∙cosx+2cos2x=0
Вариант 10:
1) Cos13x= 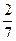
2) 3sin2x-5sinx-2=0
3) sin2x+4sinx∙cosx+3cos2x=0
Вариант 11:
1) cosx=- 
2) 2cos2x-5cosx+2=0
3) 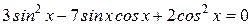
Вариант 12:
1) 3tgx- 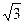 =0
=0
2) 2cos2x-3cosx+1=0
3) 2sin²x + sinx·cosx - cos²x =0
Вариант 13:
1) (1-2cosx)(2sinx+1)=0
2) cos2x-9cosx+8=0
3) 2sin2x+3sinx∙cosx-2cos2x=0
Вариант 14:
1) Sin15х= 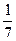
2) 4sin2x-12sinx+5=0
3) 2sin²x +7cosx +2 =0
Вариант 15:
1) cosx=- 
2) 2cos2x-sinx-1=0
3) sin²x -5sinx·cosx -6cos²x =0
Вариант 16:
1) tgx- 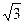 =0
=0
2) 6cos2x-sinx-1=0
3) 2sin²x -5 sinx·cosx -7 cos²x =0
Вариант 17:
1) (2cosx+ 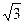 )(2sinx-
)(2sinx- 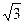 )=0
)=0
2) 2cos2x+5sinx-4=0
3) 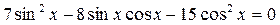
Вариант 18:
1) Sin20х= 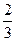
2) 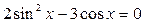
3) 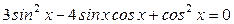
Вариант19:
1) cosx= 
2) 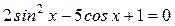
3) 2cos²x - sinx·cosx - sin²x =0
Вариант 20:
1) sinx=- 
2) 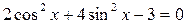
3) 2sin²x -5 sinx·cosx -7 cos²x =0
Вариант 21:
1) tgx=1
2) 3sin²x -5sinx·cosx +2cos²x =0
3) 2cos²x – cosx -1 =0
Вариант 22:
1) Sin11х= 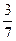
2) 3sinx+ 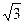 cosx=0
cosx=0
3) 4sin²x -12sinx +5 =0
Вариант 23:
1) tgx= 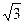
2) 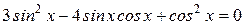
3) 4sin²x +4cosx -5 =0
Вариант 24:
1) tgx=- 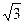
2) 2sin²x +5cosx -5 =0
3) 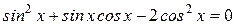
Вариант 25:
1) sinx=-1
2) 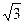 cosx -sinx =0
cosx -sinx =0
3) 3sin²x -5sinx·cosx +2cos²x =0
Вариант 26:
1) 2sinx=1
2) sinx+cosx=0
3) 8cos²x -12sinx +7 =0
Вариант 27:
1) Sin7x= 
2) 2sin2x+3sinx∙cosx-2cos2x=0
3) cos²x – 3cosx -4 =0
Вариант 28:
1) Sin78x=0
2) 3sin2x-5sinx∙cosx+2cos2x=0
3) 4 cos²x +4cosx -3 =0
Вариант 29:
1) cos8x=0
2) 2sin2x-5sinx∙cosx-7cos2x=0
3) 2sin²x – 3sinx +1 =0
Вариант 30:
1) 2cosx=-1
2) sin2x+4sinx∙cosx+3cos2x=0
3) sin²x + 3sinx +2 =0








