«Определение перемещений и напряжений в модели пускового устройства расчетным и экспериментальным
Московский Государственный технический университет имени Н.Э. Баумана
Факультет СМ «Специальное машиностроение»
Кафедра СМ8 «Стартовые ракетные комплексы»
ОТЧЕТ О ВЫПОЛНЕНИИ ЛАБОРАТОРНЫХ РАБОТ
по дисциплине «Строительная механика наземного оборудования»
«Определение перемещений и напряжений в модели пускового устройства расчетным и экспериментальным
методом»
Выполнил: Рокосовский К.С.
Плотников И.С.
Группа: СМ8-72
Преподаватель: Языков А.В.
Москва 2015
ЛАБОРАТОРНАЯ РАБОТА СМНО-2.
ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ И НАПРЯЖЕНИЙ В
МОДЕЛИ РАСЧЕТНЫМ МЕТОДОМ
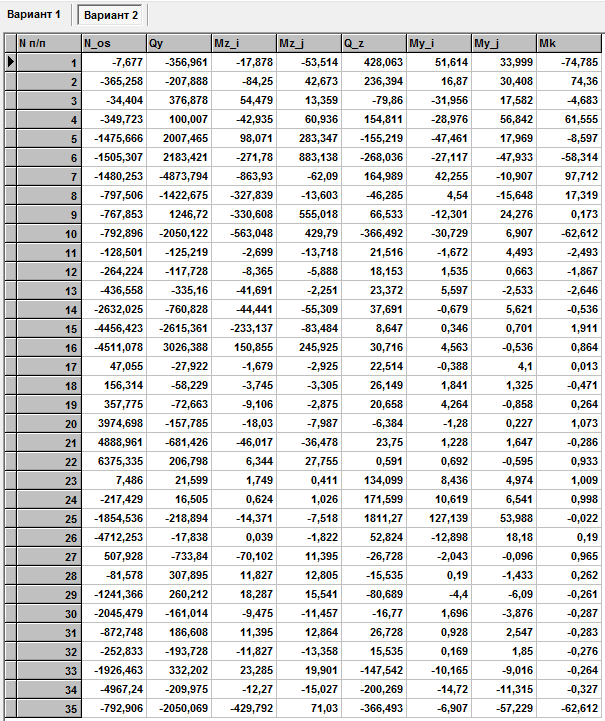
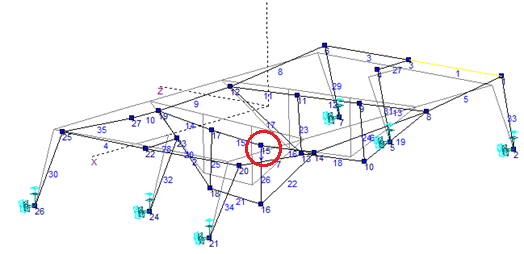
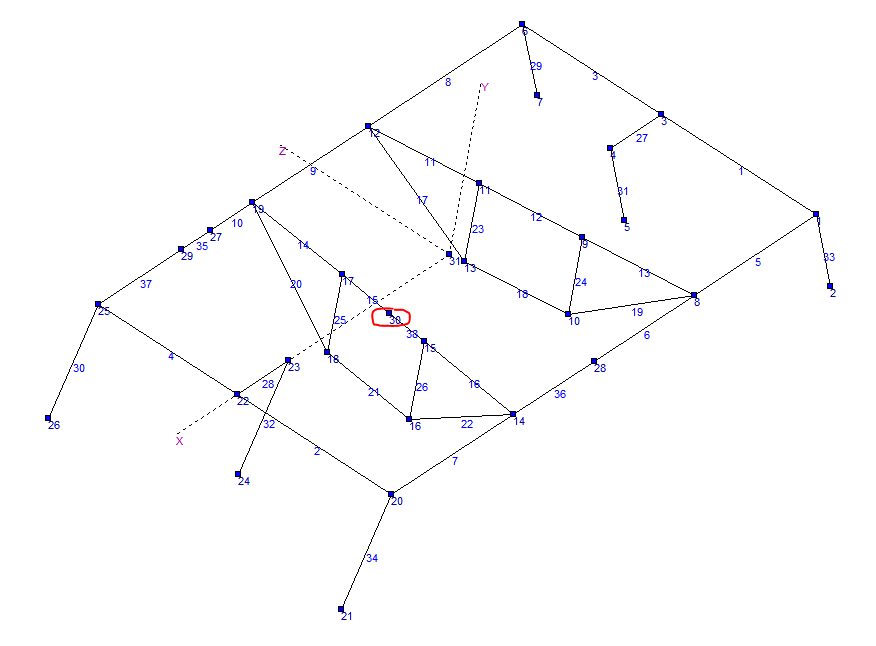
1. Исходная расчетная схема (ИРС)
Модель рамной листовой конструкции имеет весьма сложную форму. Многочисленные вырезы, компенсирующие их местные подкрепления, формируют локальные факторы, существенно искажающие линейный характер распределения нормальных напряжений (деформаций) в элементах рамы. Исследование расчётным путем напряжённо-деформированного состояния конструкций такого рода даже, применением ЭВМ представляет весьма сложную задачу.
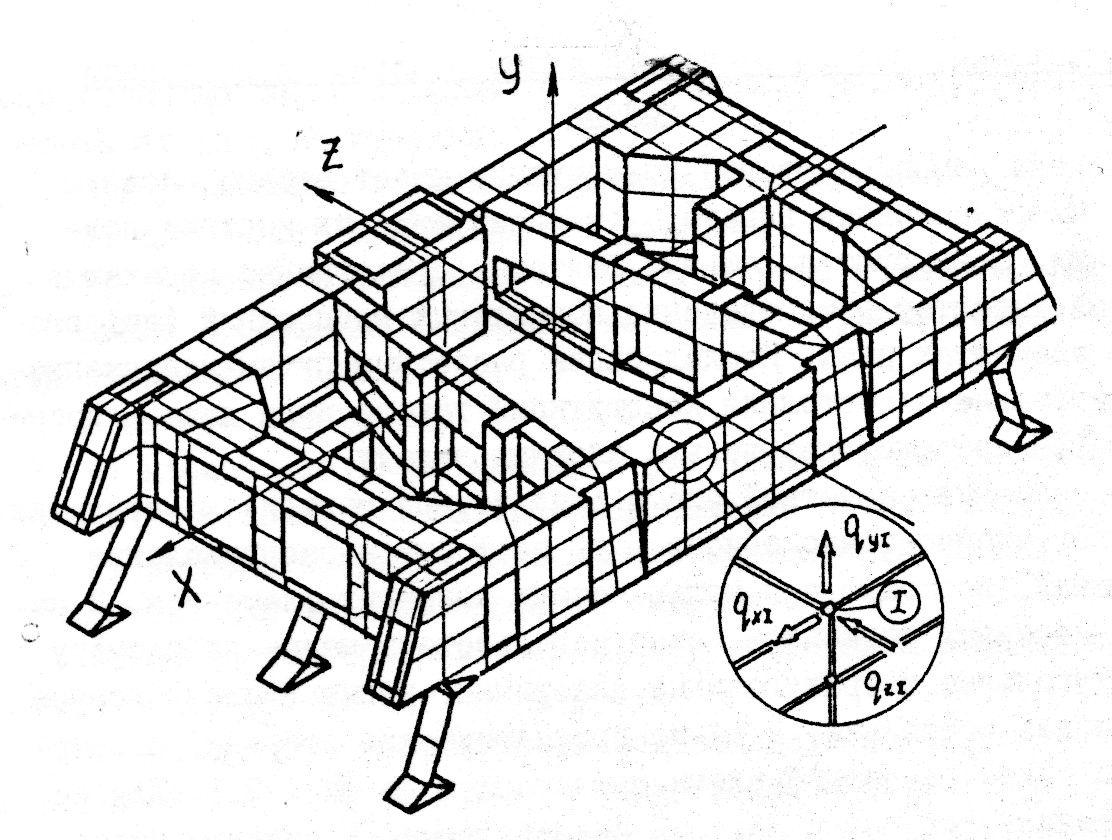 Построение расчётной схемы (физической модели) конструкции рамы, достаточно точно описывающей ее форму и распределение напряжений, возможно с помощью метода конечных элементов. В качестве конечных элементов можно использовать малые по размеру четырёхугольные и треугольные пластинки, испытывающие плоское напряженное состояние, а также призматические стержни. Ниже представлен примерный вид такой расчётной схемы.
Построение расчётной схемы (физической модели) конструкции рамы, достаточно точно описывающей ее форму и распределение напряжений, возможно с помощью метода конечных элементов. В качестве конечных элементов можно использовать малые по размеру четырёхугольные и треугольные пластинки, испытывающие плоское напряженное состояние, а также призматические стержни. Ниже представлен примерный вид такой расчётной схемы.
В ряде практических случаев, однако, оказывается важным определить в первую очередь с достаточной точностью жёсткостные характеристики конструкций, матрицу податливости или матрицу жёсткости. Жёсткостные свойства определяются перемещениями от заданных нагрузок, а перемещения в свои очередь складываются из деформаций по всему объему конструкций. Поэтому для расчета жёсткостных характеристик часто применяют упрощённые расчётные схемы, правильно отражающие основные особенности формы конструкции, а распределение усреднённых деформаций по сечениям и длинам ее элементов. При этом элементы конструкции сложной геометрии заменяют простыми, например, призматическими стержнями, имеющими эквивалентные характеристики сечений. При назначении эквивалентных геометрических характеристик элементов той или иной конструкции весьма ценным является опыт сопоставления результатов расчёта по упрощенной схеме похожей конструкции с результатами ее экспериментального исследования.
Для более точного расчета напряжений в элементах конструкции (с учетом вырезов и других локальных факторов) часто бывает достаточно провести расчёт по подробной схеме только отдельно взятых элементов. Для этого принимают характер их нагружения по границам с соседними элементами на основе результатов расчёта всей конструкции по упрощённой схеме.
Ниже изображена упрощённая расчётная схема конструкции (физическая модель).
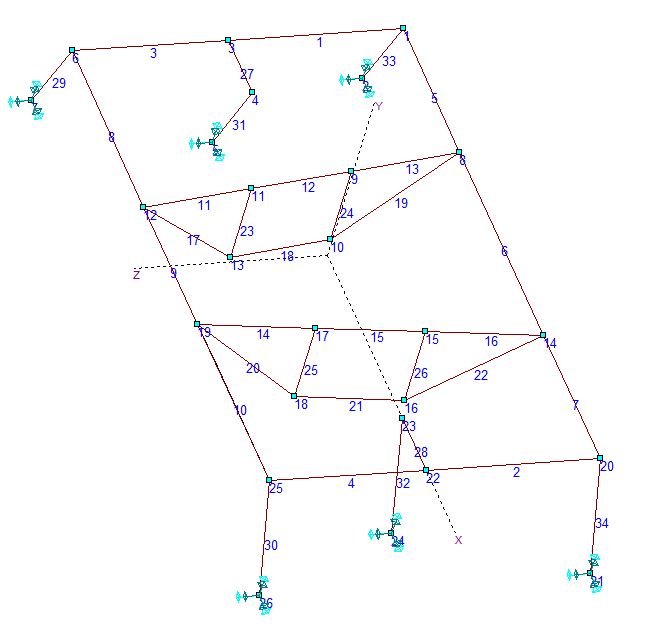
Она представляет собой пространственную симметричную стержневую систему. Все узлы схемы являются жёсткими телами, соединёнными между собой призматическими стержнями, которые можно считать конечными элементами. Положение в пространстве каждого узла характеризуется при отсутствии внешних сил тремя декартовыми координатами глобальной системы XYZ. Положение начала координат глобальной системы и направление ее осей принято с учётом симметрии расчётной схемы.
Декартовы координаты узлов и характеристики сечений призматических стержней назначаются с учётом геометрических особенностей реальной конструкции и математической модели, лежащей в основе алгоритма вычислительной программы.
Расчёт модели конструкции по упрощённой схеме проводится на ЭВМ с помощью вычислительного программного комплекса “Sadas”, реализующего метод перемещений.
Алгоритмом вычислительного комплекса предусмотрено, что внутренние силовые факторы стержня в двух взаимно перпендикулярных плоскостях (изгибающие моменты, крутящий момент, поперечные и продольная силы) являются независимыми.
Для выполнения этого условия оси инерции каждого призматического стержня (y и z) должны проходить через центр тяжести сечения, а продольная ось x должна проходить через центры узлов, соединяемых стержнями. Оси x продольных балок конструкции и смежных с ними поперечных стержней не всегда пересекаются в одной точке. Поэтому при назначении координат узлов соответствующего фрагмента расчётной схемы придётся несколько исказить форму конструкции. Аналогичные допущения должны быть сделаны и в отношении узлов, соединяющих стойки, продольные и поперечные балки.
2. Исходные данные ИРС
а) Координаты узлов:
| № узла | X, м | Y, м | Z, м | № узла | X, м | Y, м | Z, м | |
| 1 | -0,33 | 0 | -0,2 | 14 | 0,14 | 0 | -0,2 | |
| 2 | -0,38 | -0,12 | -0,2 | 15 | 0,123 | 0 | -0,07 | |
| 3 | -0,33 | 0 | 0 | 16 | 0,123 | -0,1 | -0,07 | |
| 4 | -0,25 | 0 | 0 | 17 | 0,107 | 0 | 0,05 | |
| 5 | -0,3 | -0,12 | 0 | 18 | 0,107 | -0,1 | 0,05 | |
| 6 | -0,33 | 0 | 0,18 | 19 | 0,09 | 0 | 0,18 | |
| 7 | -0,38 | -0,12 | 0,18 | 20 | 0,33 | 0 | -0,02 | |
| 8 | -0,14 | 0 | -0,2 | 21 | 0,38 | -0,12 | -0,02 | |
| 9 | -0,123 | 0 | -0,07 | 22 | 0,33 | 0 | 0 | |
| 10 | -0,123 | -0,1 | -0,07 | 23 | 0,25 | 0 | 0 | |
| 11 | -0,107 | 0 | 0,05 | 24 | 0,3 | -0,12 | 0 | |
| 12 | -0,9 | 0 | 0,18 | 25 | 0,33 | 0 | 0,18 | |
| 13 | -0,107 | -0,1 | 0,05 | 26 | 0,38 | -0,12 | 0,18 |
б) информация о стержнях:
| № стержня | Узел I | Узел J | Индекс | № стержня | Узел I | Узел J | Индекс | |
| 1 | 1 | 3 | 912 | 18 | 10 | 13 | 5 | |
| 2 | 20 | 22 | 912 | 19 | 8 | 10 | 5 | |
| 3 | 3 | 6 | 934 | 20 | 18 | 19 | 5 | |
| 4 | 22 | 25 | 934 | 21 | 16 | 18 | 5 | |
| 5 | 1 | 8 | 2 | 22 | 14 | 16 | 5 | |
| 6 | 8 | 14 | 2 | 23 | 11 | 13 | 6 | |
| 7 | 14 | 20 | 2 | 24 | 9 | 10 | 6 | |
| 8 | 12 | 6 | 2 | 25 | 17 | 18 | 6 | |
| 9 | 12 | 19 | 909 | 26 | 15 | 16 | 6 | |
| 10 | 19 | 25 | 2 | 27 | 3 | 4 | 6 | |
| 11 | 11 | 12 | 4 | 28 | 23 | 22 | 7 | |
| 12 | 9 | 11 | 4 | 29 | 6 | 7 | 7 | |
| 13 | 8 | 9 | 4 | 30 | 25 | 26 | 7 | |
| 14 | 17 | 19 | 4 | 31 | 4 | 5 | 7 | |
| 15 | 15 | 17 | 4 | 32 | 23 | 24 | 7 | |
| 16 | 14 | 15 | 4 | 33 | 1 | 2 | 7 | |
| 17 | 13 | 12 | 5 | 34 | 20 | 21 | 7 |
в) индексы стержней:
| № п/п | Индекс | Материал | Тип сеч. | Мод. сеч. I | Мод. cеч. J | Угол |
| 1 | 2 | 8 | 50 | 1 | 1 | 0 |
| 2 | 4 | 8 | 50 | 2 | 2 | 0 |
| 3 | 5 | 8 | 50 | 3 | 3 | 0 |
| 4 | 6 | 8 | 50 | 4 | 4 | 0 |
| 5 | 7 | 8 | 50 | 1 | 1 | 0 |
| 6 | 909 | 8 | 909 | 1 | 1 | 0 |
| 7 | 912 | 8 | 912 | 1 | 1 | 0 |
| 8 | 934 | 8 | 934 | 1 | 1 | 0 |
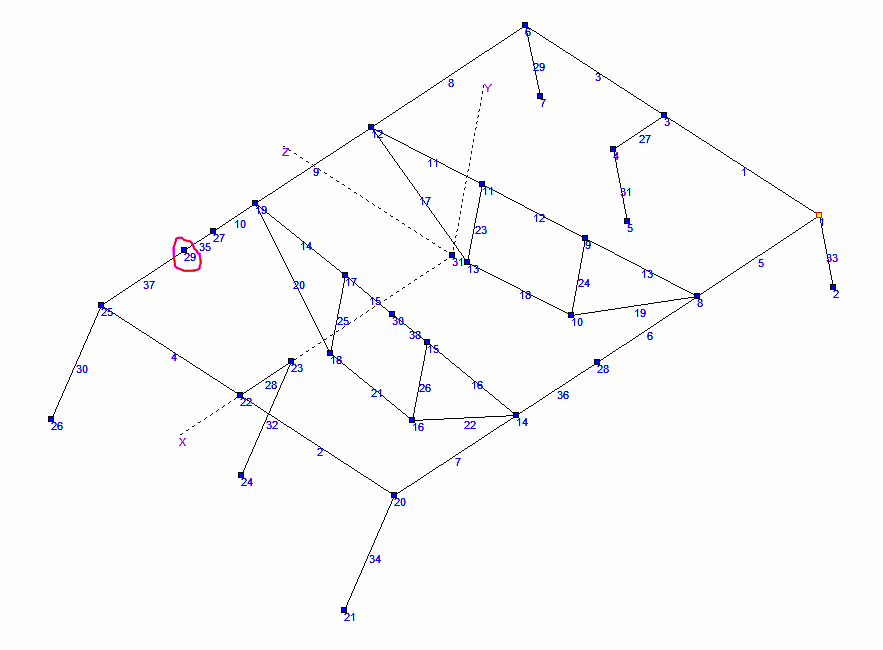
3. Принятая расчетная схема (ПРС)
Одна из нагрузок будет приложена в точке, лежащей между узлами 19 и 25, поэтому для проведения расчетов в упрощенную расчетную схему конструкции была введен дополнительный узел 27 (см. рис. ниже). Он разделил стержень 10 на два новых стержня: 10 и 35.
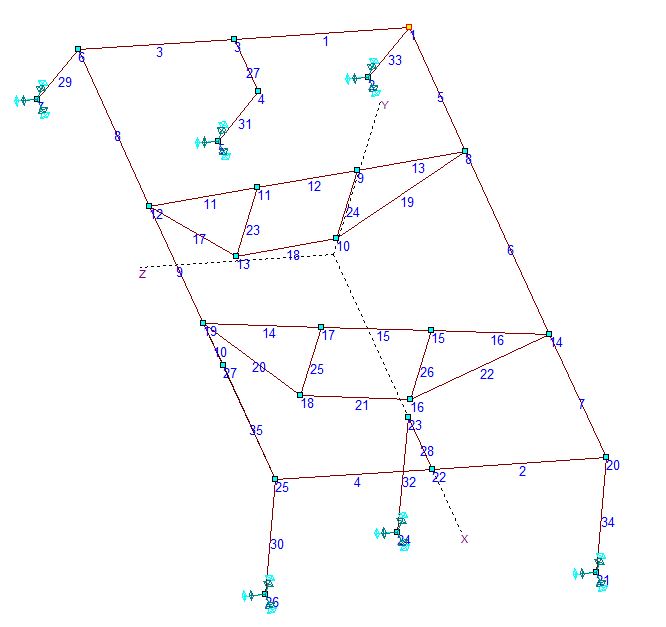
4. Исходные данные ПРС
а) Координаты узлов:
| № узла | X, м | Y, м | Z, м | № узла | X, м | Y, м | Z, м | |
| 1 | -0,33 | 0 | -0,2 | 14 | 0,14 | 0 | -0,2 | |
| 2 | -0,38 | -0,12 | -0,2 | 15 | 0,123 | 0 | -0,07 | |
| 3 | -0,33 | 0 | 0 | 16 | 0,123 | -0,1 | -0,07 | |
| 4 | -0,25 | 0 | 0 | 17 | 0,107 | 0 | 0,05 | |
| 5 | -0,3 | -0,12 | 0 | 18 | 0,107 | -0,1 | 0,05 | |
| 6 | -0,33 | 0 | 0,18 | 19 | 0,09 | 0 | 0,18 | |
| 7 | -0,38 | -0,12 | 0,18 | 20 | 0,33 | 0 | -0,02 | |
| 8 | -0,14 | 0 | -0,2 | 21 | 0,38 | -0,12 | -0,02 | |
| 9 | -0,123 | 0 | -0,07 | 22 | 0,33 | 0 | 0 | |
| 10 | -0,123 | -0,1 | -0,07 | 23 | 0,25 | 0 | 0 | |
| 11 | -0,107 | 0 | 0,05 | 24 | 0,3 | -0,12 | 0 | |
| 12 | -0,9 | 0 | 0,18 | 25 | 0,33 | 0 | 0,18 | |
| 13 | -0,107 | -0,1 | 0,05 | 26 | 0,38 | -0,12 | 0,18 | |
| 27 | 0, 155 | 0 | 0, 18 | |||||
б) информация о стержнях:
| № стержня | Узел I | Узел J | Индекс | № стержня | Узел I | Узел J | Индекс | |
| 1 | 1 | 3 | 0 | 18 | 10 | 13 | 5 | |
| 2 | 20 | 22 | 0 | 19 | 8 | 10 | 5 | |
| 3 | 3 | 6 | 1 | 20 | 18 | 19 | 5 | |
| 4 | 22 | 25 | 1 | 21 | 16 | 18 | 5 | |
| 5 | 1 | 8 | 2 | 22 | 14 | 16 | 5 | |
| 6 | 8 | 14 | 2 | 23 | 11 | 13 | 6 | |
| 7 | 14 | 20 | 2 | 24 | 9 | 10 | 6 | |
| 8 | 12 | 6 | 2 | 25 | 17 | 18 | 6 | |
| 9 | 12 | 19 | 3 | 26 | 15 | 16 | 6 | |
| 10 | 19 | 27 | 2 | 27 | 3 | 4 | 6 | |
| 11 | 11 | 12 | 4 | 28 | 23 | 22 | 7 | |
| 12 | 9 | 11 | 4 | 29 | 6 | 7 | 7 | |
| 13 | 8 | 9 | 4 | 30 | 25 | 26 | 7 | |
| 14 | 17 | 19 | 4 | 31 | 4 | 5 | 7 | |
| 15 | 15 | 17 | 4 | 32 | 23 | 24 | 7 | |
| 16 | 14 | 15 | 4 | 33 | 1 | 2 | 7 | |
| 17 | 13 | 12 | 5 | 34 | 20 | 21 | 7 | |
| 35 | 27 | 25 | 2 | |||||
в) индексы стержней остались без изменения.
5. Расчет геометрических характеристик сечений
При назначении эквивалентных геометрических характеристик сечений призматических стержней приходится также принимать ряд допущений. Эти допущения должны касаться характера распределения напряжений по сечениям и длине элементов конструкции, а также формы элементов.
Можно предположить, что при деформации сечения элементов конструкции остаются плоскими. Это обстоятельство позволяет принять линейный закон распределения нормальных напряжений в сечениях, а распределение касательных напряжений изгиба считать равномерным по толщине независимо от того, является ли профиль сечения открытым или замкнутым.
Наибольшие трудности возникают при назначении эквивалентных характеристик сечений призматических стержней, идеализирующих поперечные балки модели и участок продольной балки, содержащий коробчатую вставку. Эти элементы имеют весьма сложную форму.
В соответствии с упрощённой схемой поперечную балку необходимо представить двумя призматическими стержнями, а коробчатую вставку – одним. Эквивалентные характеристики стержня могут быть заданы с учётом характера эпюр внутренних силовых факторов. Можно предположить, что в пределах некоторых длин участков a, b, c и так далее характеристики сечений балки и изгибающие моменты являются неизменными.
Для расчета характеристик стержней и коробчатой вставки, они были разделены на ряд сечений: стержень 1 и 2 – сечения Г-Г и Д-Д; стержень 3 и 4 – сечения Б-Б и В-В; стержень 9 – сечения Ж-Ж, И-И и К-К. После чего для каждого сечения были посчитаны геометрические характеристики: главные моменты инерции Jz, Jy, момент инерции при кручении Jk, площадь F.
Данные геометрических характеристик были рассчитаны каждой группой в отдельности по каждому сечению.
Сечение Б-Б:
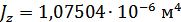
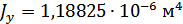
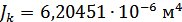
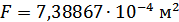
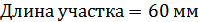
Сечение В-В:
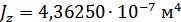
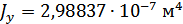
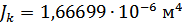
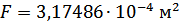
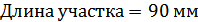
Сечение Г-Г:
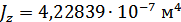
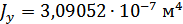
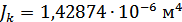
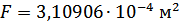
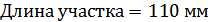
Сечение Д-Д:
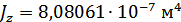
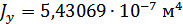
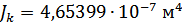
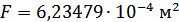
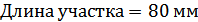
Сечение Ж-Ж:
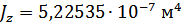
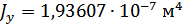
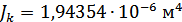
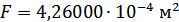
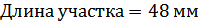
Сечение И-И:
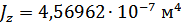
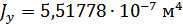
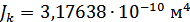
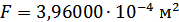
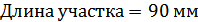
Сечение К-К:
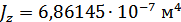
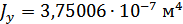
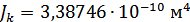
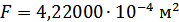
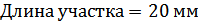
Тогда, приравняв потенциальную энергию деформации изгиба рассматриваемой части поперечной балки в плоскости xy соответствующей энергии деформации призматического стержня, можно получить
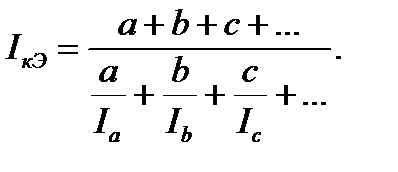
Таким образом, можно предварительно определить 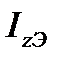 и
и 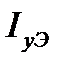 по последней формуле, а затем, выполнив расчёт, их уточнить и провести расчёт вторично. Эквивалентное значение для площади определяется аналогично.
по последней формуле, а затем, выполнив расчёт, их уточнить и провести расчёт вторично. Эквивалентное значение для площади определяется аналогично.
Эквивалентные геом. характеристики для стержней 1-2 (Г-Г+Д-Д):
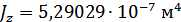
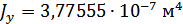
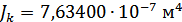
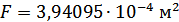
Эквивалентные геом. характеристики для стержней 3-4 (Б-Б+В-В):
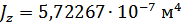
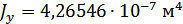
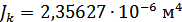
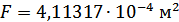
Эквивалентные геом. характеристики для стержня 9 (Ж-Ж + И-И + К-К):
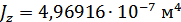
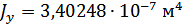
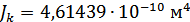
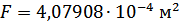
6. Результаты расчета по ПРС
После ввода всех необходимых исходные данных по стержням и рассчитанным эквивалентным сечениям, модель «нагружается» силой P =10354 Н в узлах 15 и 27. Эта сила была получена расчетным путем при выполнении экспериментального нагружения конструкции в работе СМНО-3.
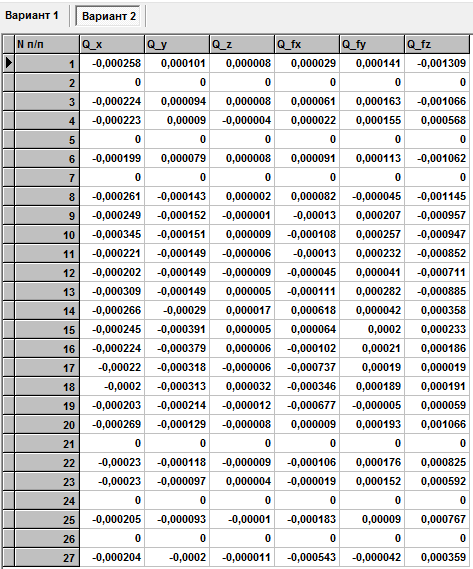
Статические перемещения от силы P , приложенной в узле 27 и коэффициенты запаса
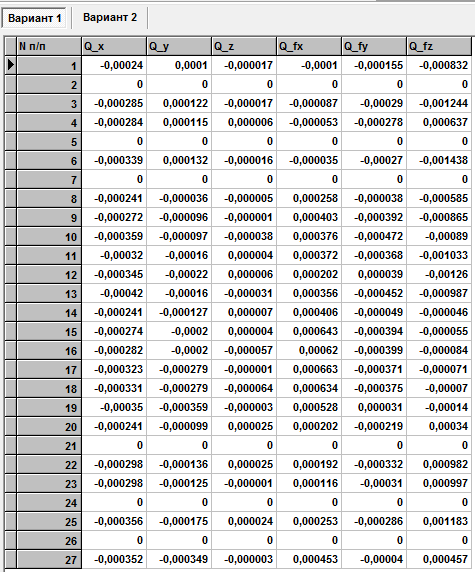
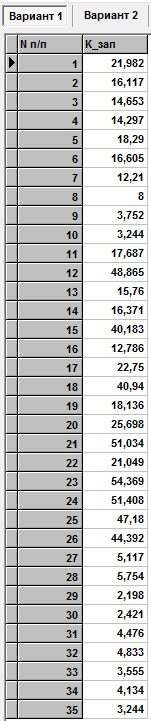
Внутренние силовые факторы в КЭ (от нагружения 27 узла)
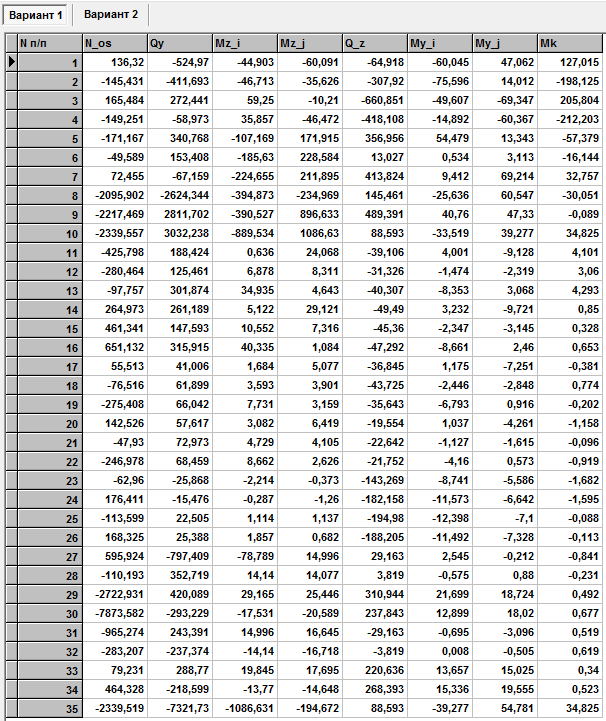
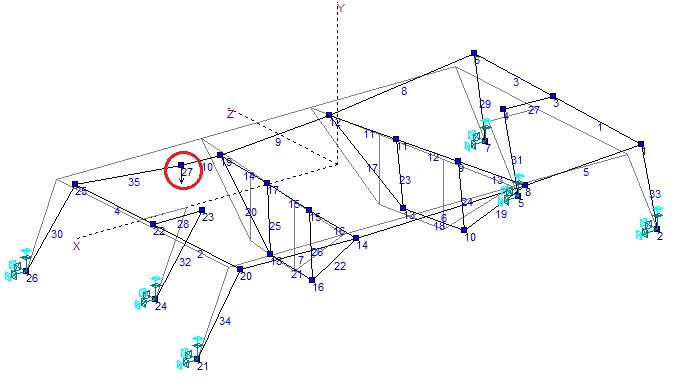
Статические перемещения от силы P , приложенной в узле 15 и коэффициенты запаса
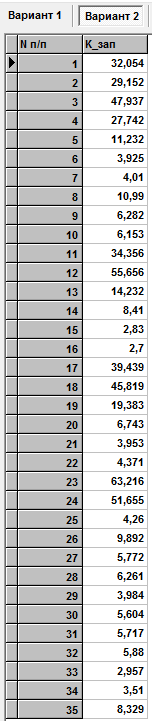
Внутренние силовые факторы в КЭ (от нагружения 15 узла)
7. Расчет напряжений
1. Первая группа тензодатчиков (тензодатчики № 1-4)
Тензодатчики первой группы измеряют напряжения на стержне №(10+35) и находятся на расстоянии 45 мм от узла №27. Для измерения напряжения в месте крепления тензодатчиков введем узел 29 на стержне №35 на расстоянии 45 мм от узла 27.
Стержень №(10+35) имеет тип сечения №050 и модификацию №1, данные которой, необходимые для дальнейших расчётов, представлены ниже.
Характеристика модификации: 95х44х1,5.
Главные моменты инерции:
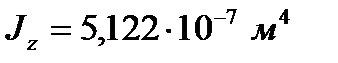
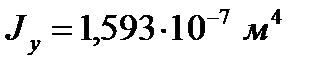
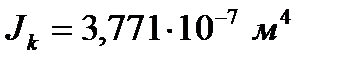
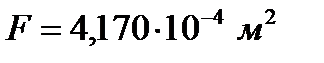
Расположение тензодатчиков по сечению:
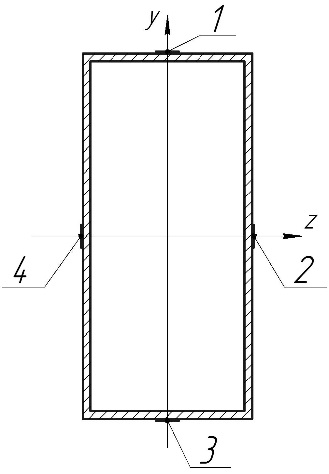
Для расчета напряжений на датчиках №1-4 воспользуемся следующими формулами:
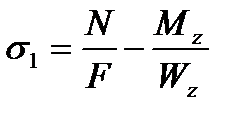
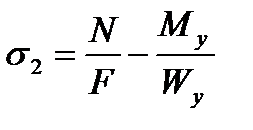
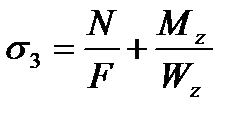
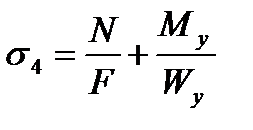
где N – осевая сила в стержне;
F – площадь стержня;
Mz – изгибающий момент по оси Z;
My – изгибающий момент по оси Y;
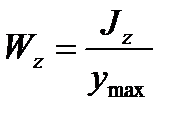 – момент сопротивления изгибу по оси Z,
– момент сопротивления изгибу по оси Z,
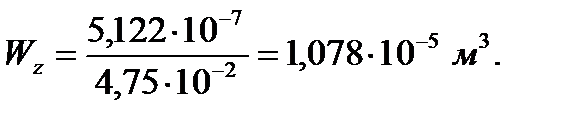
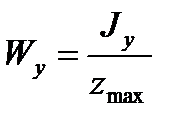 – момент сопротивления изгибу по оси Y,
– момент сопротивления изгибу по оси Y,
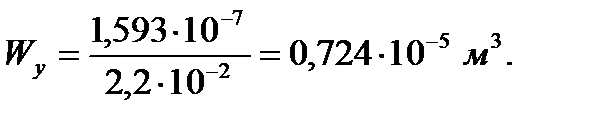
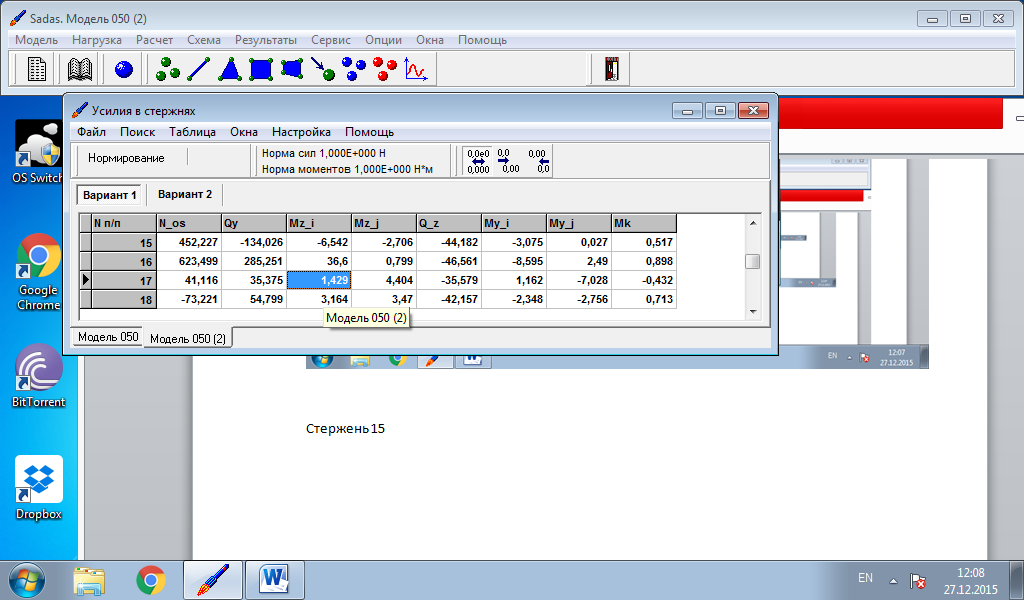
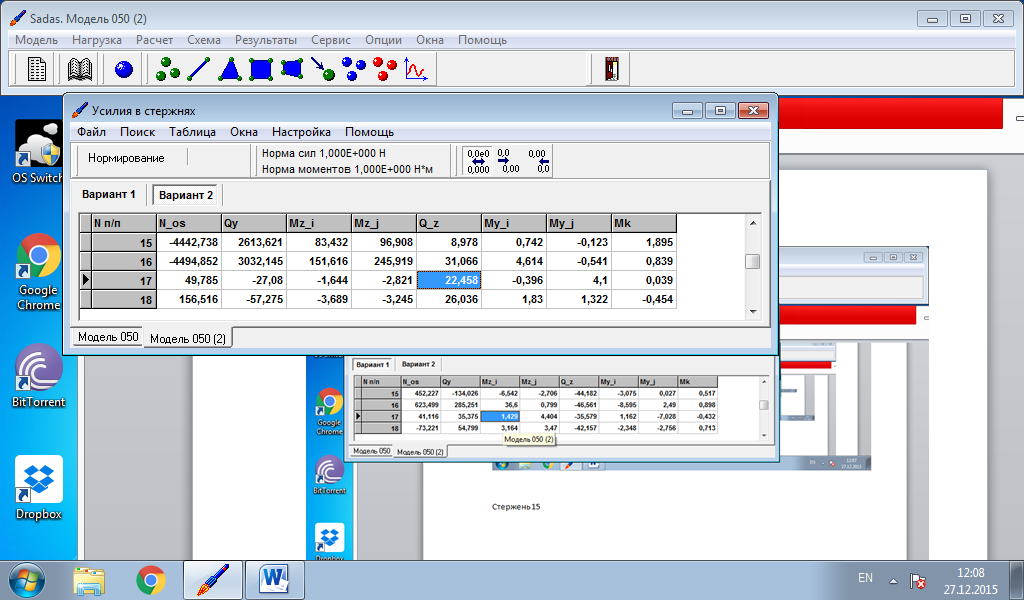
Данные об изгибающих моментах и осевой силе в стержне берем из расчетов в программе Sadas для врезанного узла 29:
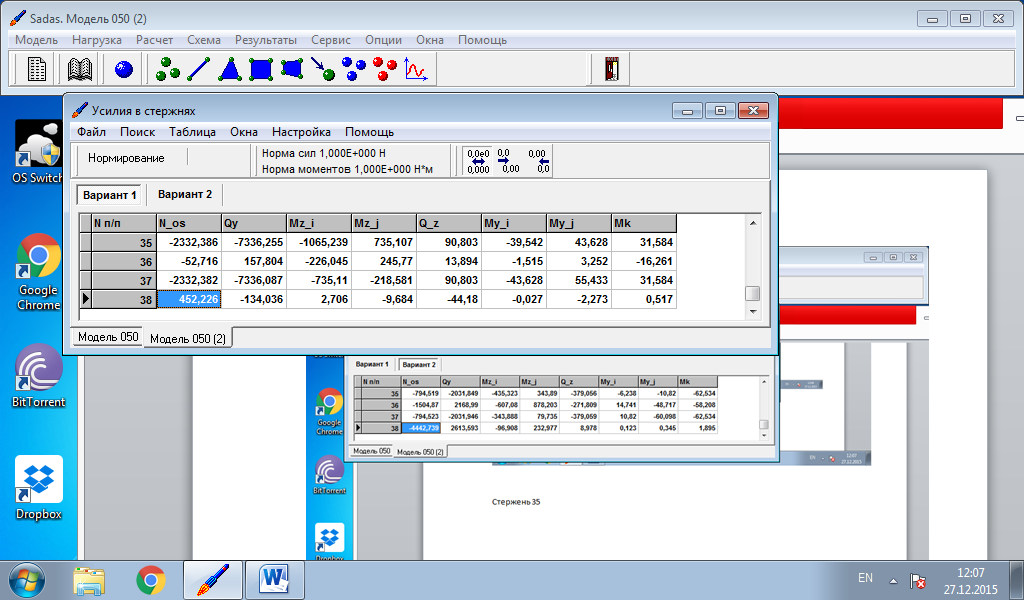
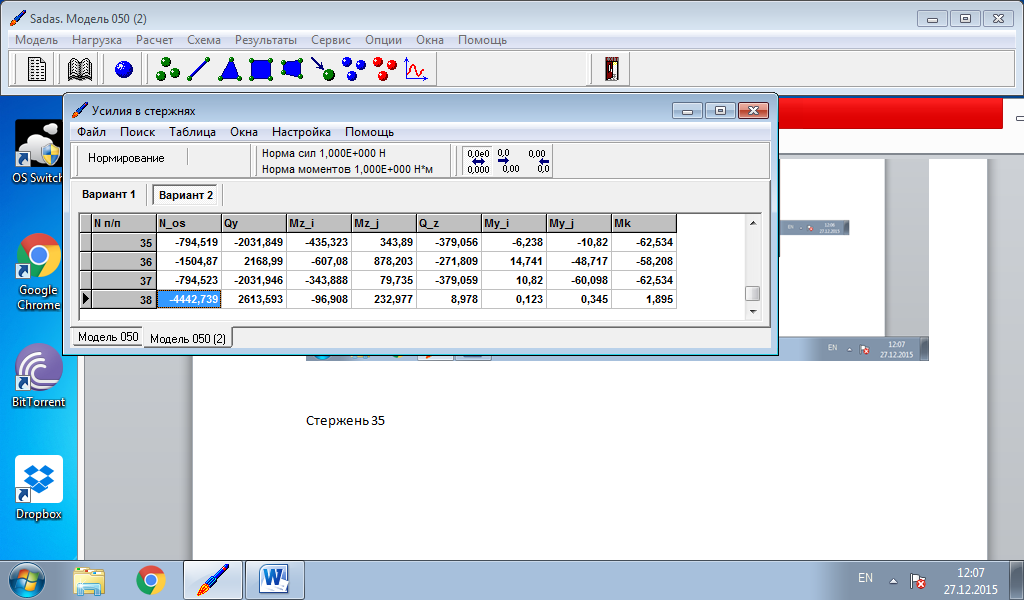
Вариант 1 – нагрузка на узел 27
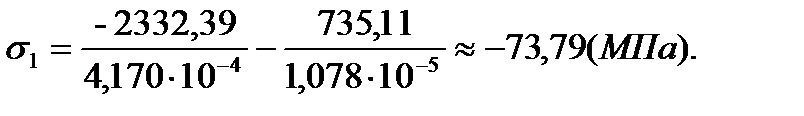
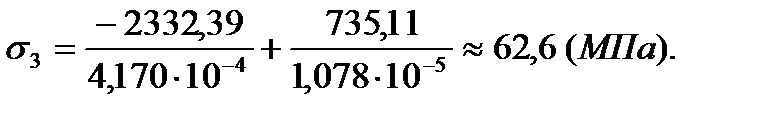
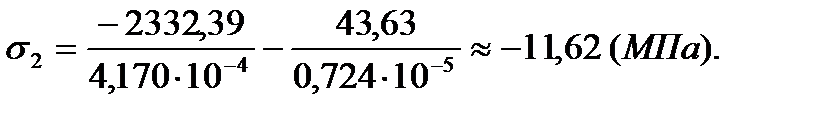
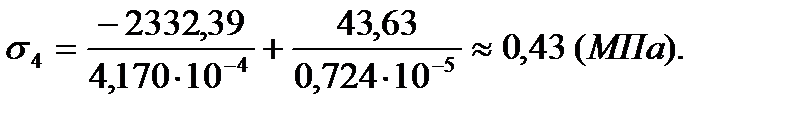
Вариант 2 – нагрузка на узел 15
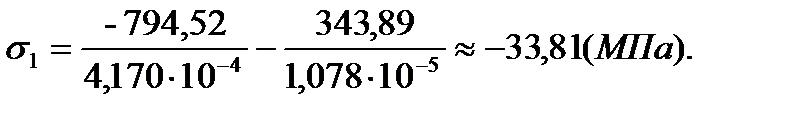
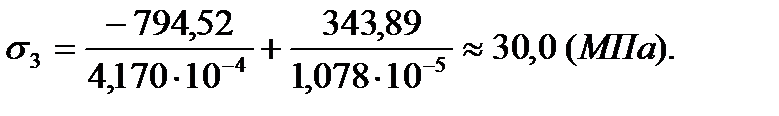
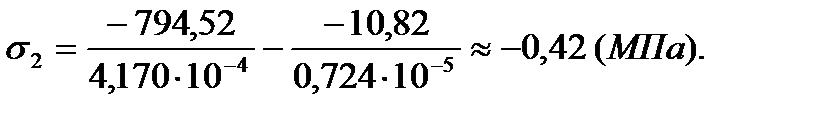
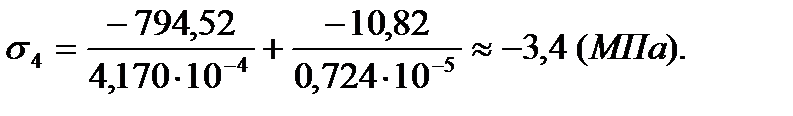
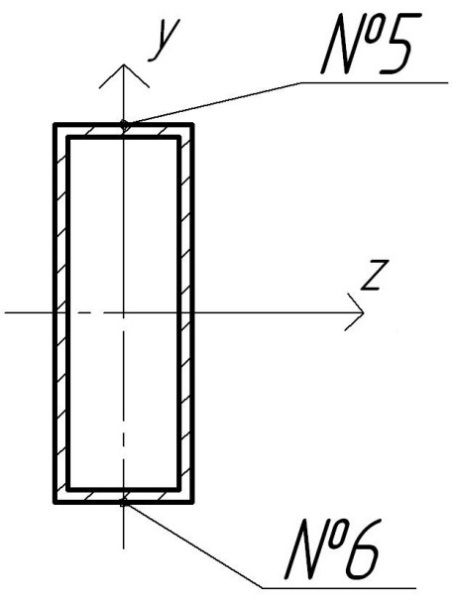
2. Вторая группа тензодатчиков (тензодатчики № 5-8)
Тензодатчики второй группы измеряют напряжения на стержне №15 и находятся на расстоянии 69 мм от узла №17. Для измерения напряжения в месте крепления тензодатчиков введем узел 30 на стержне №15 на расстоянии 69 мм от узла 17.
Стержень №15 имеет тип сечения №050 и модификацию №2, данные которой, необходимые для дальнейших расчётов, представлены ниже.
Характеристика модификации: 47х16х1,5.
Главные моменты инерции:
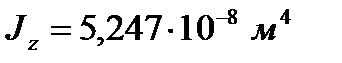
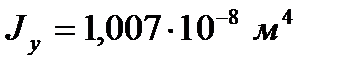
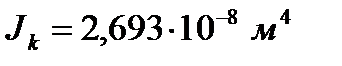
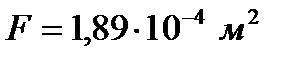
Расположение тензодатчиков по сечению:
Для расчета напряжений на датчиках №5-6 воспользуемся следующими формулами:
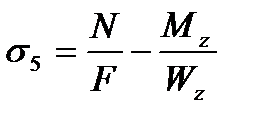
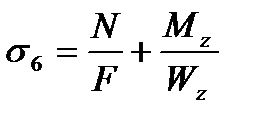
где N – осевая сила в стержне;
F – площадь стержня;
Mz – изгибающий момент по оси Z;
My – изгибающий момент по оси Y;
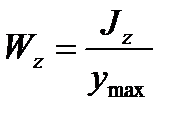 – момент сопротивления изгибу по оси Z,
– момент сопротивления изгибу по оси Z,
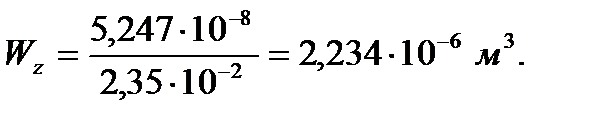
Стержень №21 имеет тип сечения №050 и модификацию №3, данные которой, необходимые для дальнейших расчётов, представлены ниже.
Характеристика модификации: 25х16х1,5.
Главные моменты инерции:
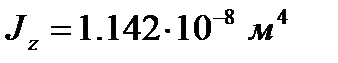
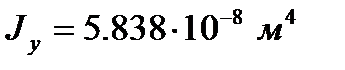
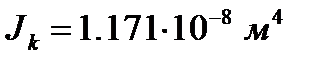
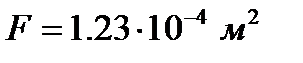
Расположение тензодатчиков по сечению:
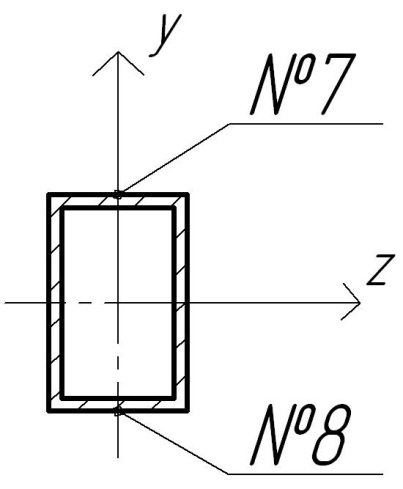
Для расчета напряжений на датчиках №7 и №8 воспользуемся следующими формулами:
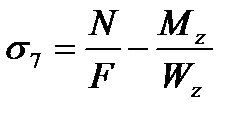
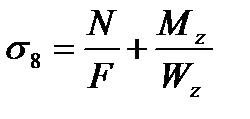
где N – осевая сила в стержне;
F – площадь стержня;
Mz – изгибающий момент по оси Z;
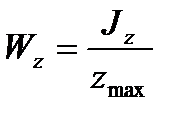 – момент сопротивления изгибу по оси Z,
– момент сопротивления изгибу по оси Z,
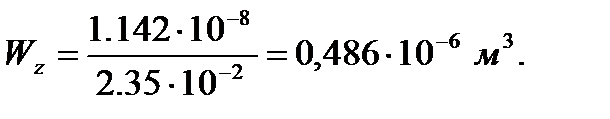
Данные об изгибающих моментах и осевой силе в стержне берем из расчетов в программе Sadas для врезанного узла 30:
Вариант 1 – нагрузка на узел 27
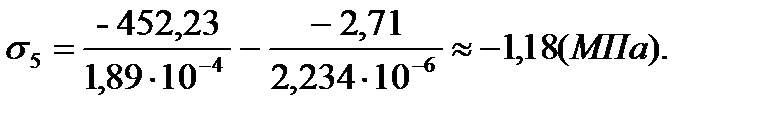
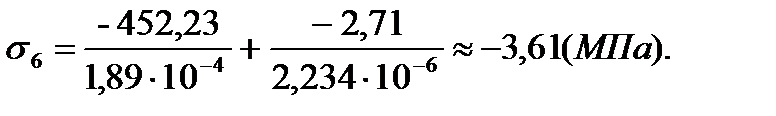
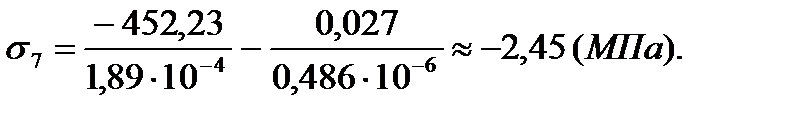
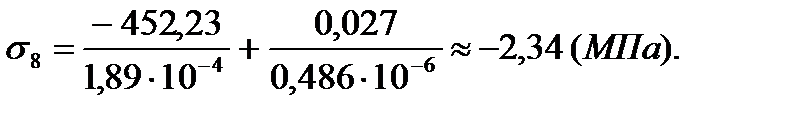
Вариант 2 – нагрузка на узел 15
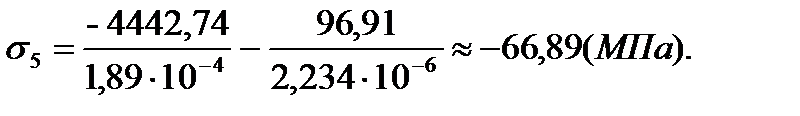
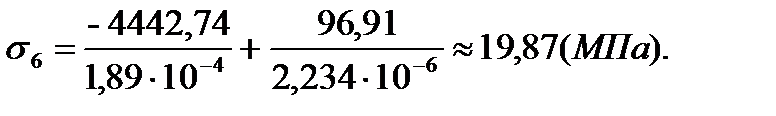
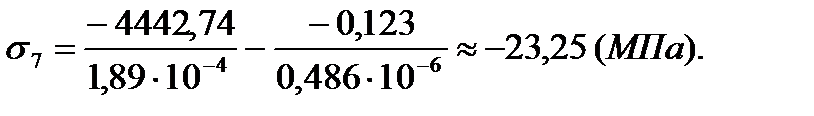
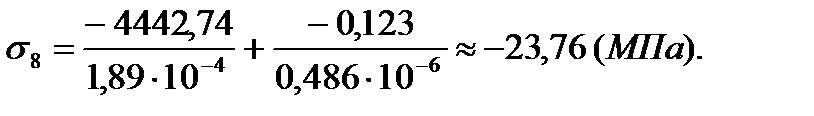
3. Третья группа тензодатчиков (тензодатчики № 9-12)
Тензодатчики третьей группы измеряют напряжения на стержне №6 и находятся на расстоянии 155 мм от узла №8. Для измерения напряжения в месте крепления тензодатчиков введем узел 28 на стержне №6 на расстоянии 155 мм от узла 8.
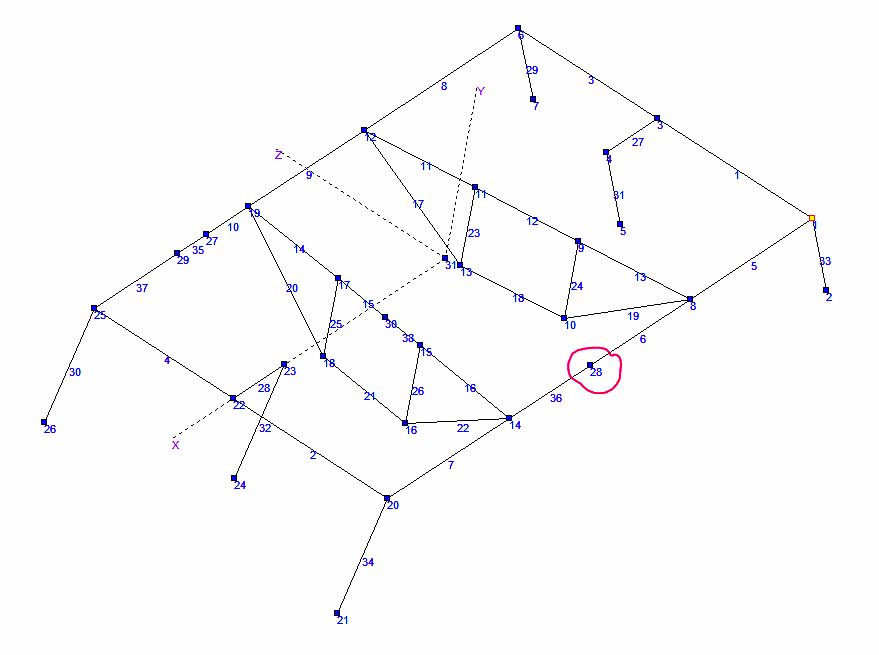
Стержень №6 имеет тип сечения №050 и модификацию №1, данные которой, необходимые для дальнейших расчётов, представлены ниже.
Характеристика модификации: 95х44х1,5.
Главные моменты инерции:
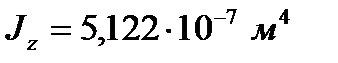
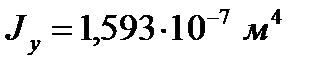
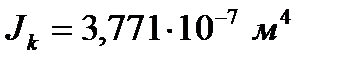
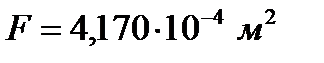
Расположение тензодатчиков по сечению:
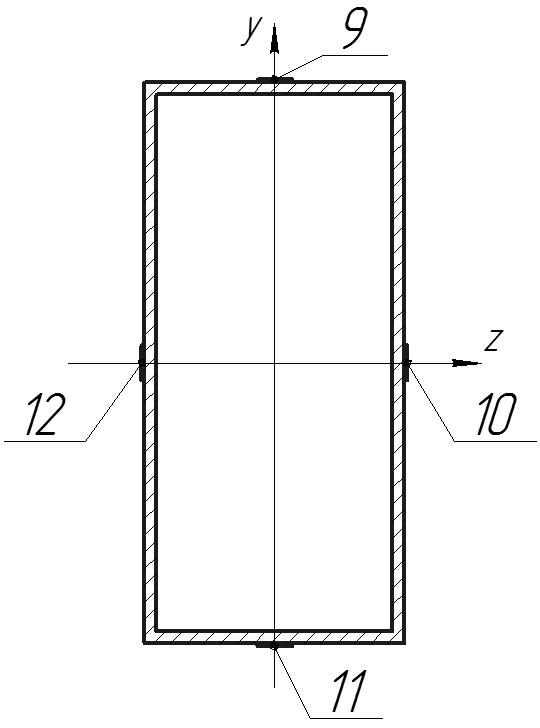
Для расчета напряжений на датчиках №9-12 воспользуемся следующими формулами:
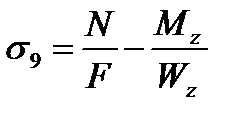
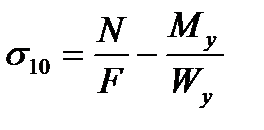
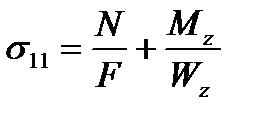
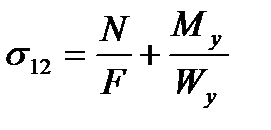
где N – осевая сила в стержне;
F – площадь стержня;
Mz – изгибающий момент по оси Z;
My – изгибающий момент по оси Y;
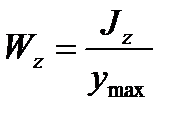 – момент сопротивления изгибу по оси Z,
– момент сопротивления изгибу по оси Z,
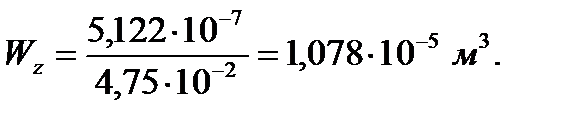
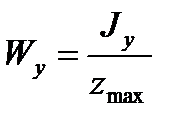 – момент сопротивления изгибу по оси Y,
– момент сопротивления изгибу по оси Y,
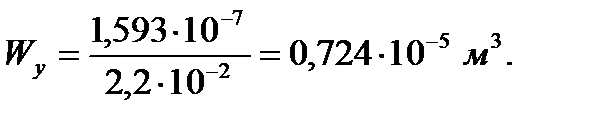
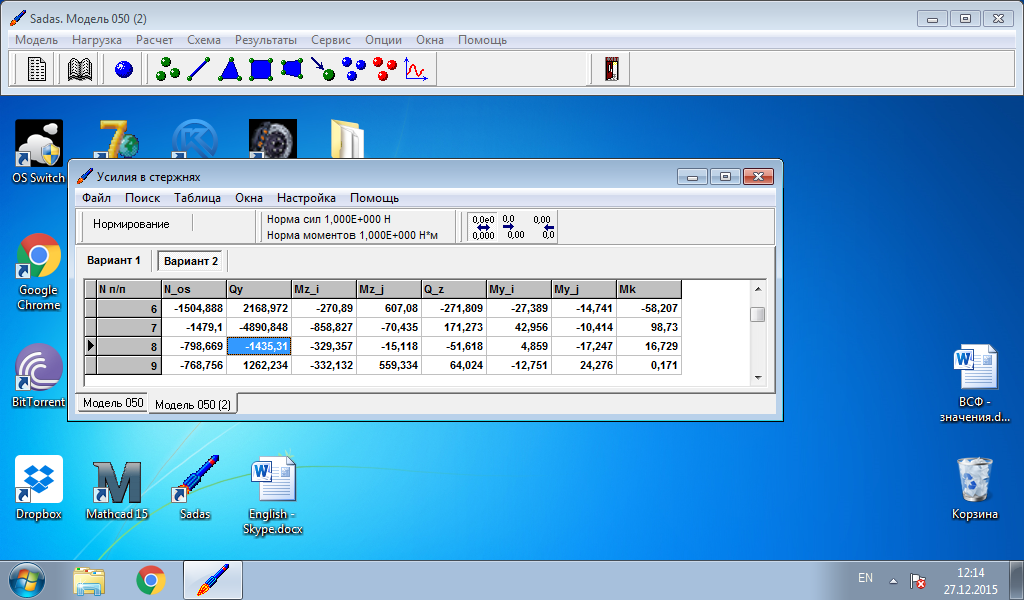
Данные об изгибающих моментах и осевой силе в стержне берем из расчетов в программе Sadas для врезанного узла 28:
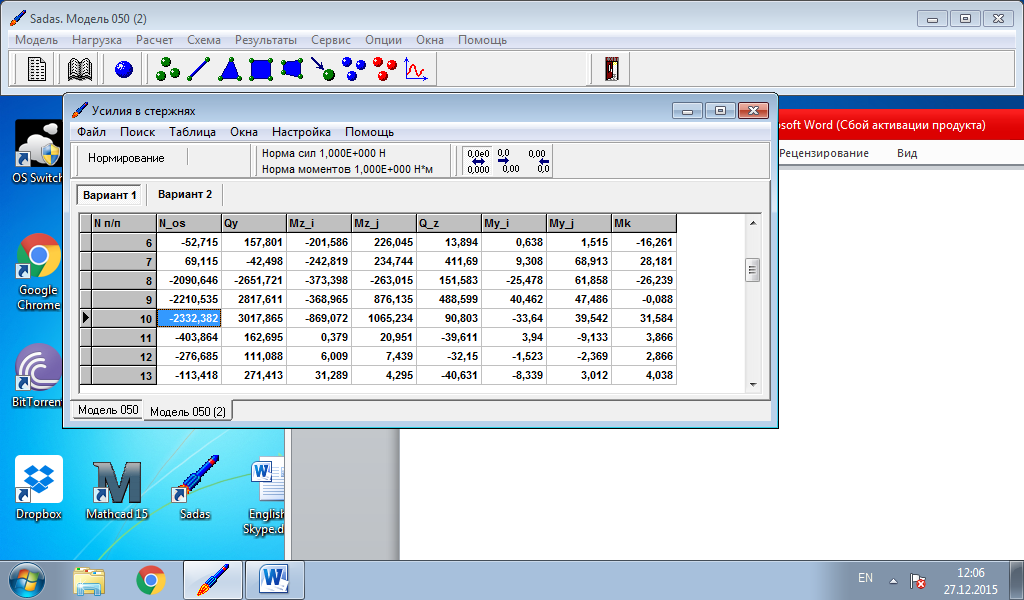
Вариант 1 – нагрузка на узел 27
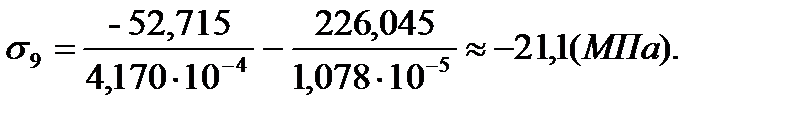
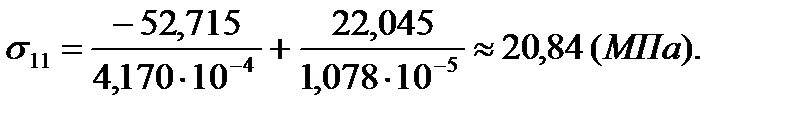
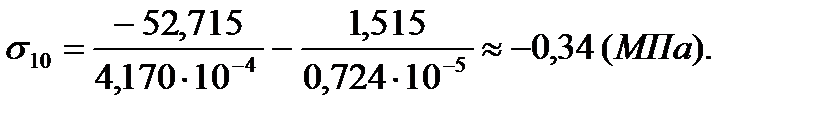
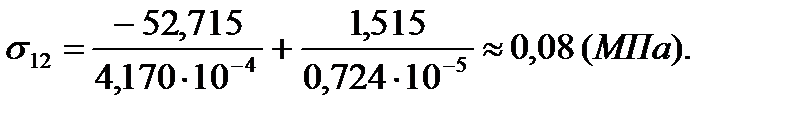
Вариант 2 – нагрузка на узел 15
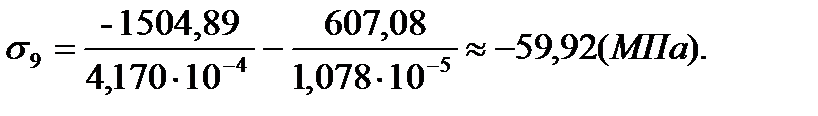
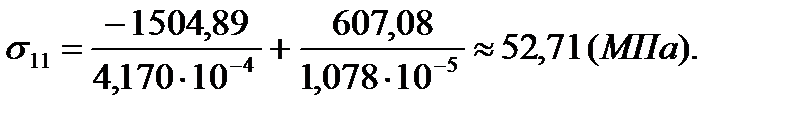
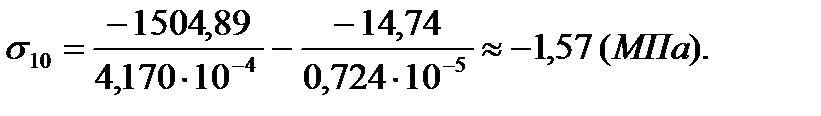
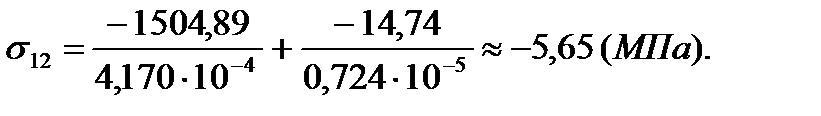
8. Сравнение расчетных и экспериментальных данных
8.1 Перемещения в узлах
8.1.1 Нагружение узла 27:
0,13 мм - Sadas (узел №14)
0,021 мм - экспериментальное значение для узла №14
0,36 мм - Sadas (узел №19)
0,72 мм - экспериментальное значение для узла №19
8.1.2 Нагружение узла 15:
0,29 мм - Sadas (узел №14)
0,37 мм - экспериментальное значение для узла №14
0,21 мм - Sadas (узел №19)
0,21 мм - экспериментальное значение для узла №19
8.2 Напряжения
| № тензодатчика | Нагрузка на 27 узел | Нагрузка на 15 узел | ||
| Расчет | Эксперимент | Расчет | Эксперимент | |
| 1 | -73,79 | -41,6 | -33,81 | -7,0 |
| 2 | 0,43 | -0,35 | -0,42 | 0,001 |
| 3 | 62,6 | 18,05 | 30,0 | 4,0 |
| 4 | -11,62 | -1,22 | -3,4 | -0,75 |
| 5 | -1,18 | 0,36 | -66,89 | -5,4 |
| 6 | -3,61 | 0,35 | 19,87 | 0,18 |
| 7 | -2,45 | -0,3 | 23,25 | 6,6 |
| 8 | -2,34 | 0,6 | 23,76 | 8,15 |
| 9 | -21,1 | -3,1 | -59,92 | -15,7 |
| 10 | 0,08 | 0,8 | -1,57 | 1,53 |
| 11 | 20,84 | 3,2 | 52,71 | 12,5 |
| 12 | -0,34 | -1,2 | -5,65 | -3,6 |
ЛАБОРАТОРНАЯ РАБОТА СМНО-3.
Тензометрия – экспериментальное определение напряженного состояния конструкций, основанное на измерении местных деформаций.
1. Тарировка тензодатчиков
1.1 Цели тарировки:
Целью тарировки является нахождение тарировочных коэффициентов, которые позволяют найти соответствие между электрическим сигналом с тензодатчиков и действительными деформациями (напряжениями) модели. Тарировка производится посредством сравнения, полученного со стенда электрического сигнала с теоретическими напряжениями в точке максимального прогиба.
Для тарировки используется тарировочный стенд, который позволяет производить нагружение конструкции, а также с помощью установленных на модель тензодатчиков определять деформации модели.
1.2. Устройство тензорезистора
Тензорезистор – представляет собой плоскую зигзагообразную спираль из тонкой проволоки или травленой фольги. Спираль вклеивается между двумя бумажными или пластмассовыми лепестками. Применяются тензорезисторы для измерения упругих и остаточных деформаций поверхности конструкции, материал которой работает как в пределах, так и за пределами упругости. Широко применяются тензодатчики типа фольговых тензорезисторов, которые при деформации изменяют свое сопротивление. Тензодатчик приклеивается к модели так, чтобы база lp была ориентирована вдоль измеряемого напряжения. Фольговые тензорезисторы отличаются относительной простотой изготовления и в равной степени пригодны для измерения упругих и упругопластических деформаций при статических и динамических нагрузках.
Для точного измерения напряжений необходимо иметь датчики малой базы. Особенно это важно для конструкций малых размеров с вырезами, имеющих большие градиенты напряжений. Однако недостатком тензодатчиков малой базы ( lp <5 мм) является существенное влияние на их продольные деформации вдоль базы поперечных деформаций, фиксируемых петлями проволоки датчиков, имеющих диаметры закруглений, соизмеримые с базой.
1.3 Принцип работы тензорезистора.
Из закона Гука, напряжение:
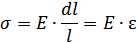
где, E – модуль упругости, 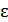 – относительная деформация.
– относительная деформация.
Сопротивление проводника рассчитывается по формуле:
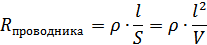
где: 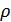 – удельное сопротивление,
– удельное сопротивление, 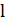 – длина, S- поперечное сечение.
– длина, S- поперечное сечение.
Величина чувствительности:
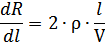
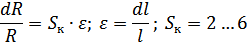
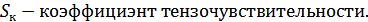
В рабочей зоне тензоризистора его сопротивление изменяется на очень малую величину.
Как известно, температура достаточно сильно влияет на удельную проводимость всех материалов, это в полной мере касается и материалов, из которых изготовлен тензодатчик.
Для компенсации изменения проводимости в зависимости от температуры применяется схема подключения, по типу резисторного моста, когда один из тензорезисторов не установлен на модели, а находится от неё на небольшом расстоянии, что позволяет учесть изменение температуры окружающей среды.
1) 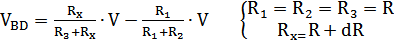
2) 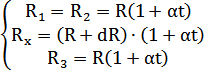
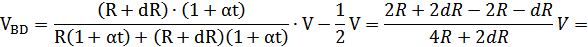
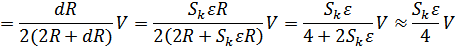
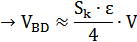
1.4. Устройство тарировочного стенда.
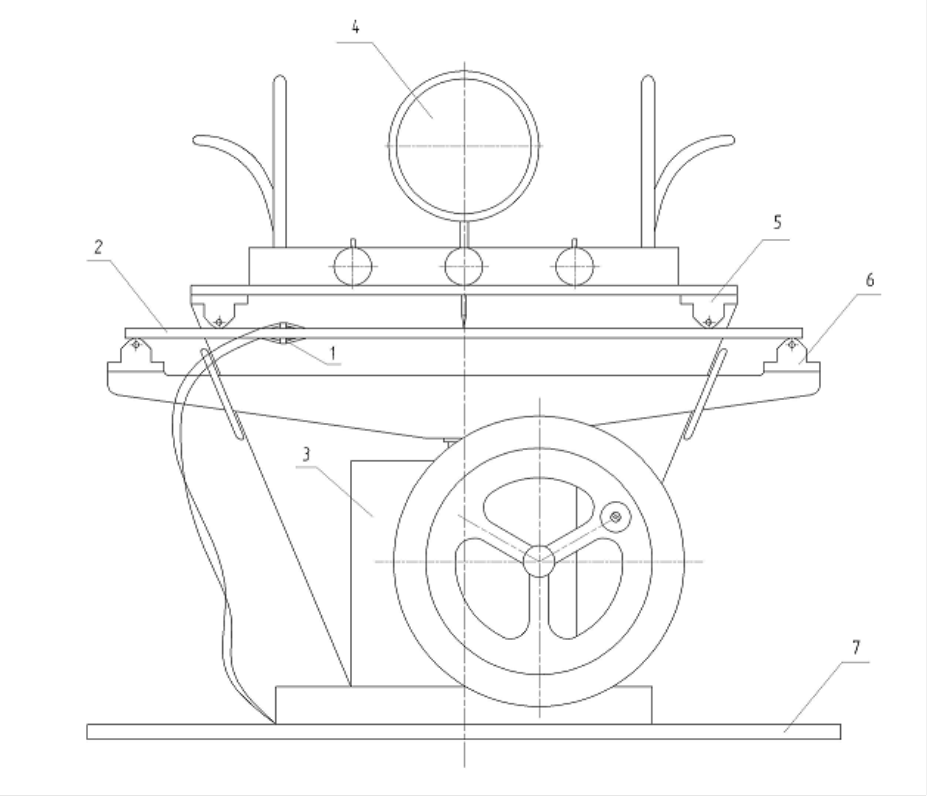
1 — тензодатчики;
2 — балка;
3 — червячный механизм;
4 — индикатор часового типа;
5 — опоры, передающие нагрузку с червячного механизма;
6 — опоры;
7 — станина.
Состав тарировочного стенда:
- ЭВМ - предназначена для получения результатов от измерительной системы, их записи и дальнейшей обработке;
- Распаячная коробка - служит для согласования подключения тензорезисторов к измертельному оборудованию, а также для установки элементов термокомпенсации.;
- Измерительное оборудование - предназначено для измерения и преобразования сигналов с датчиков - из аналоговой в цифровую.;
- Комплект датчиков (тензорезисторов) - предназначен для преобразования измерительной величины (механического напряжения) в параметры электрической цепи.
Параметры балки были сняты с модели путем измерения штангенциркулем и линейкой и имеют следующие значения: a=0,03м; b=0.006м; l=0.365м (см рисунок 1.2.)
рис. 1.2.
1.5. Расчет коэффициента k
Расчетная схема:
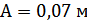
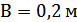
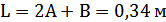
Коэффициент k устанавливает зависимость между перемещением и напряжением:
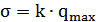
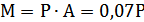
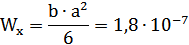
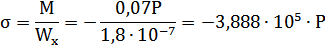
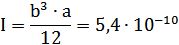
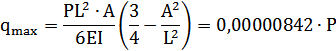
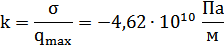
1.6. Определение тарировочного коэффициента
Расчет для группы №5
Балке последовательно передавались перемещения 0.5, 1(мм) на нагрузку и разгрузку. Результаты, снятые с ЭВМ приведены в таблице:
| Перемещение, мм | 
| 
|
| 0 | -37 | 43 |
| 0,5 | 2830 | -2828 |
| 1 | 5543 | -5532 |
| 0,5 | 2822 | -2838 |
| 0 | 46 | -30 |
Далее определяется зависимость напряжения для каждого перемещения от полученных параметров:
| 0,0005 | 0,001 | 0,0005 |
| 2830 | 5543 | 2822 |
| -2828 | -5532 | -2838 |
2,31· 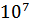
| 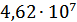
| 2,31· 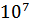
|
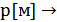
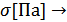
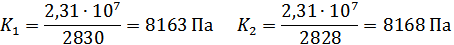
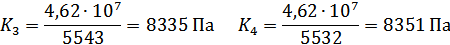
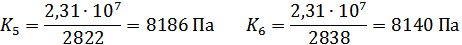
Из полученных значений находим среднее: 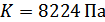
Вычислив значения К для всех групп, выбираем из средний результат:
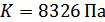
2. Эксперимент
2.1. Принцип работы стенда
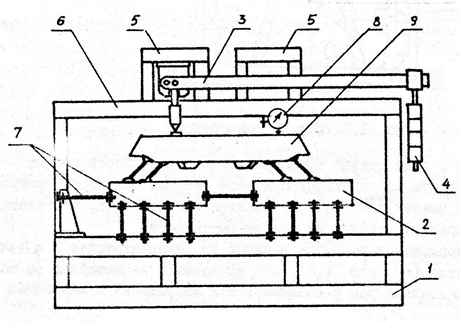
Испытательный стенд состоит из нижней (1) и верхней (6) рам, двух опорных плит (2), двух тумб (5), установленных на верхней раме, и двух нагрузочных устройств (3) рычажного типа, смонтированных на тумбах, с соотношением плеч каждого рычага 1:40. Нагружение модели (9) осуществляется подвешиванием грузов (4) на штангу рычага. Вес каждого груза - 20 Н, а максимальное количество грузов, подвешиваемых на одну штангу - 10. Таким образом, нагрузка на модель может меняться ступенчато. Для крепления индикаторов перемещения на верхней и нижней рамах стенда имеются кронштейны (8) с зажимами.
2.2. Схема модели
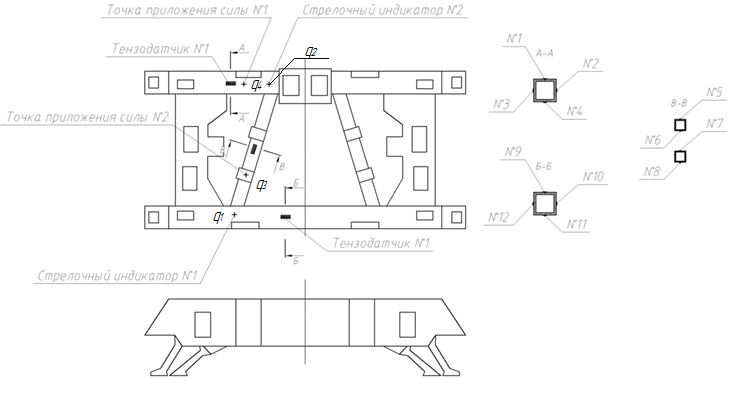
Исследуемая модель представляет собой металлическую листовую сварную конструкцию с большим количеством вырезов, ребер и других подкрепляющих элементов, опирающуюся на шесть наклонных стоек. Стойки прикреплены к двум опорным плитам, соединенным между собой и с нижней рамой стенда горизонтальными и вертикальными стержнями. Стержни позволяют регулировать положение плит относительно нижней рамы стенда и модели.
Плиты и рамы стенда представляют в совокупности весьма жесткую опорную конструкцию. При этом высокая жесткость соединения, плит с нижней рамой обеспечивается за счет того, что стержни работают преимущественно на сжатие-растяжение.
При приложении нагрузки в одной из заданных точек модель деформируется, что приводит к перемещению ее точек относительно рам и возникновению напряжений в элементах конструкции. Перемещения точек фиксируются с помощью индикаторов, а для исследования напряженно-деформированного состояния конструкции в соответствующих точках наклеиваются тензодатчики. Для измерения перемещений точек модели относительно рам и опорных плит применяются стрелочные индикаторы часового типа с максимальной величиной хода штока - 5 мм. Индикаторы имеют цену деления, равную 0,01 мм, и позволяют измерить перемещении точек модели с точностью до 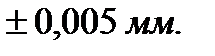
2.3. Проведение эксперимента
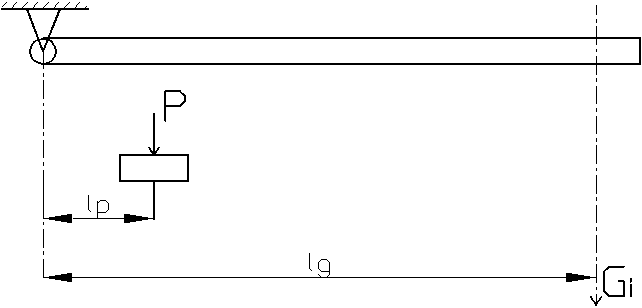
Схема нагружения конструкции представлена на рисунке ниже.
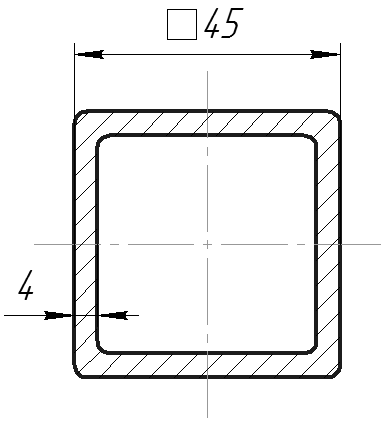
Сечение рычага:
Массово-геометрические характеристики рычага приведены в таблице 1
Таблица 1
| a,мм | 45 | ρ, кг/м3 | 7900 |
| h,мм | 4 | V,м3 | 1,36E-03 |
| Lg,м | 2,08 | M, кг | 11,68 |
| F,м2 | 6,56E-04 | ∆P, Н | 2350 |
Сила нагружения для данной схемы определяется по следующей формуле:
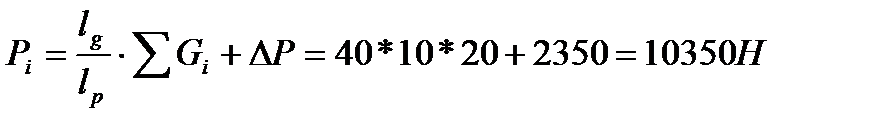
где Pi – сила нагружения;
Gi – вес одного груза, по условию Gi=20 Н;
DР – вес рычага, по условию DР=2350 Н;
lg/lp = 40 – отношение длин.
2.4. Результаты эксперимента
Значения перемещений:
| Индикатор 19 (мм) | Индикатор 14 (мм) | ||||
| Нагрузка (Н) | Нагрузка на 27 узел | Нагрузка на 15 узел | Нагрузка на 27 узел | Нагрузка на 15 узел | |
| 0 | 0 | 0 | 0 | 0 | 0 |
| рычаг | 2350 | 0,2 | 0,065 | 0 | 0,13 |
| 2 | 3950 | 0,3 | 0,08 | 0,005 | 0,16 |
| 4 | 5550 | 0,4 | 0,11 | 0,01 | 0,22 |
| 6 | 7150 | 0,51 | 0,14 | 0,012 | 0,27 |
| 8 | 8750 | 0,61 | 0,18 | 0,015 | 0,32 |
| 10 | 10350 | 0,72 | 0,21 | 0,021 | 0,37 |
| 8 | 8750 | 0,69 | 0,21 | 0,02 | 0,37 |
| 6 | 7150 | 0,61 | 0,2 | 0,02 | 0,37 |
| 4 | 5550 | 0,49 | 0,18 | 0,018 | 0,32 |
| 2 | 3950 | 0,36 | 0,12 | 0,015 | 0,23 |
| рычаг | 2350 | 0,25 | 0,08 | 0,01 | 0,16 |
| 0 | 0 | 0 | 0 | 0 | 0 |
Нагрузка
| Инд. 14, нагр. 27 |
| Инд. 19, нагр. 15 |
| Инд. 14, нагр. 15 |
| Инд. 19, нагр. 27 |
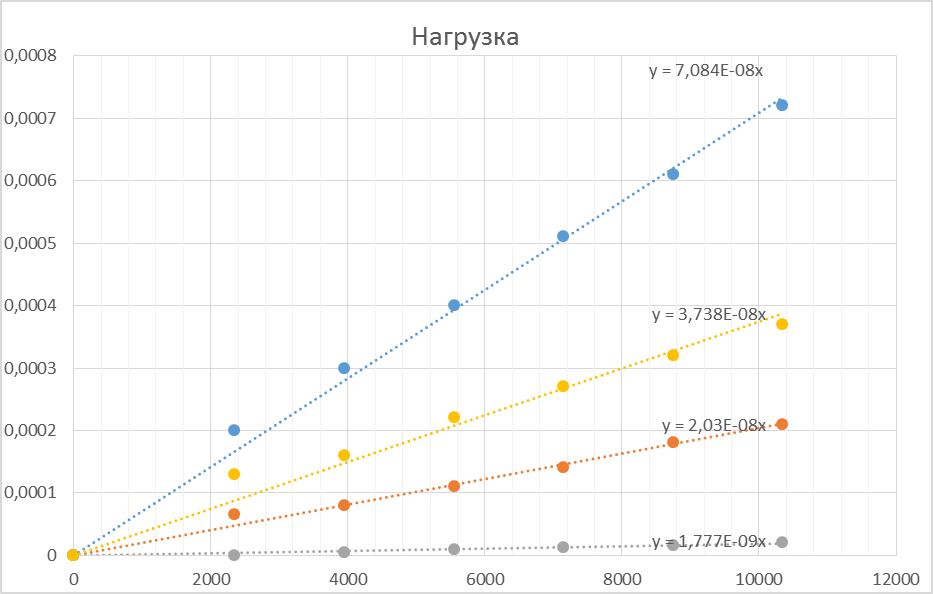
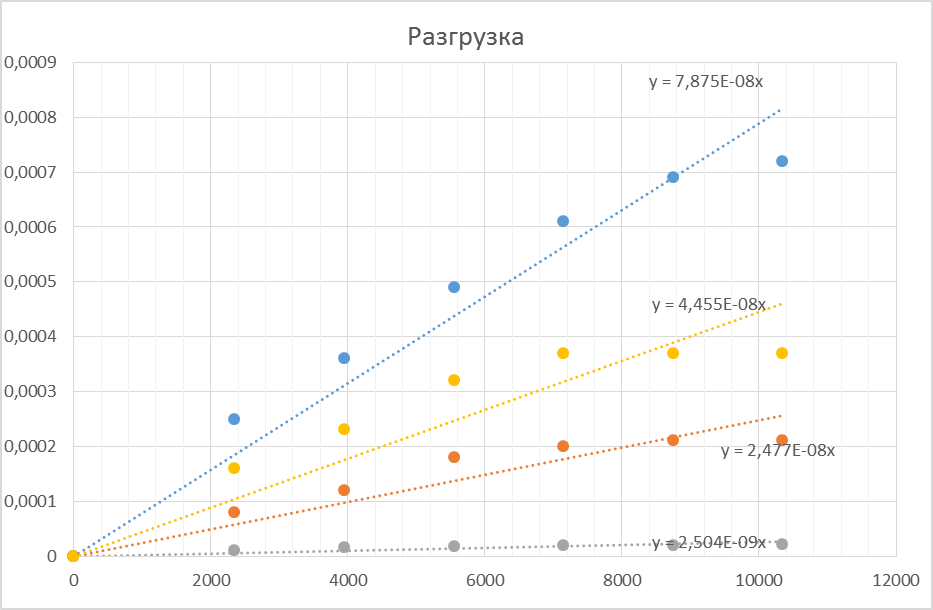
Разгрузка
| Инд. 14, нагр. 27 |
| Инд. 19, нагр. 15 |
| Инд. 14, нагр. 15 |
| Инд. 19, нагр. 27 |
2.5. Расчёт коэффициентов матрицы податливости.
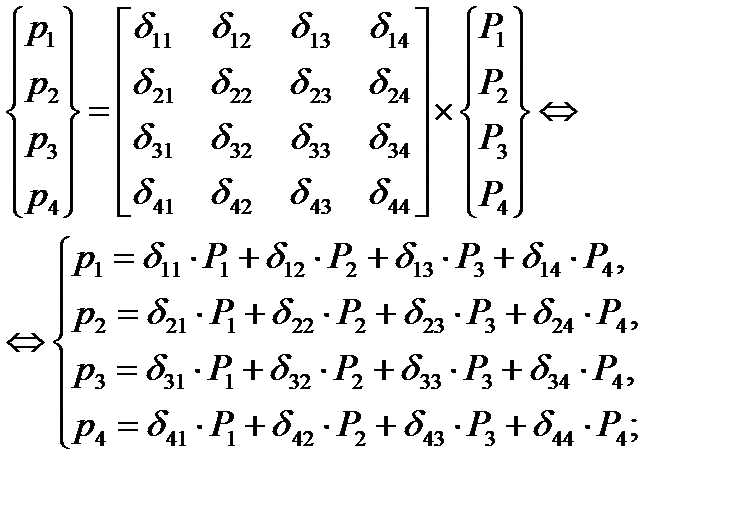
Где p1 и p2 – перемещения в точках, расположения индикаторов.
p3 и p4 – перемещения в точках, приложения внешней нагрузки при проведении эксперимента.
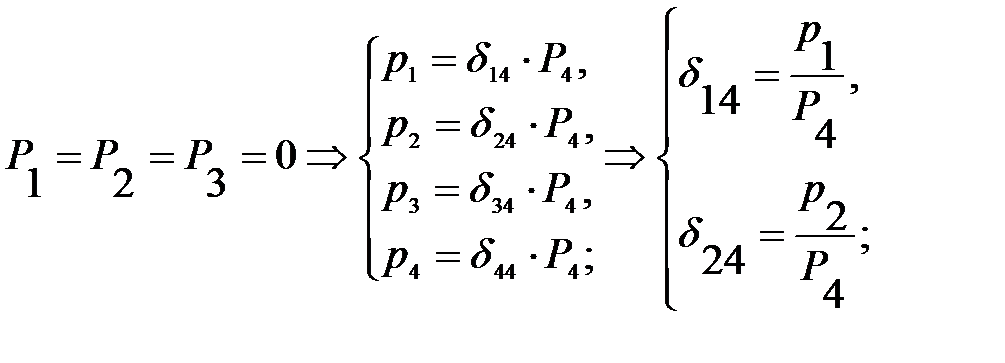
Т. к. у нас несколько значений перемещений и сил, то посчитаем средние коэффициенты матрицы податливости, для чего построим осреднённые линейные зависимости перемещений от нагрузки.
Получили зависимости (I этап):
для узла №19 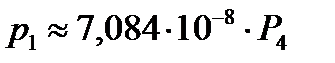 – нагрузка;
– нагрузка;
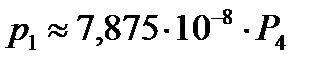 – разгрузка;
– разгрузка;
для узла №14 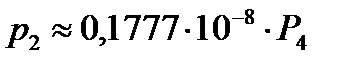 – нагрузка;
– нагрузка;
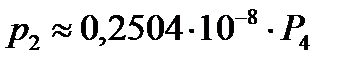 – разгрузка;
– разгрузка;
Т. е. можно принять:
для узла №19 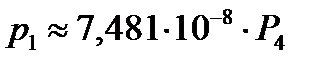 ;
;
для узла №14 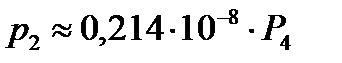 ;
;
Коэффициенты матрицы податливости равны тангенсу углов наклона полученных зависимостей, т. е.:
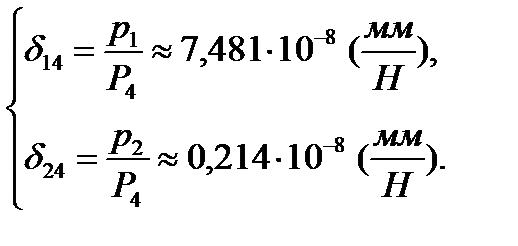
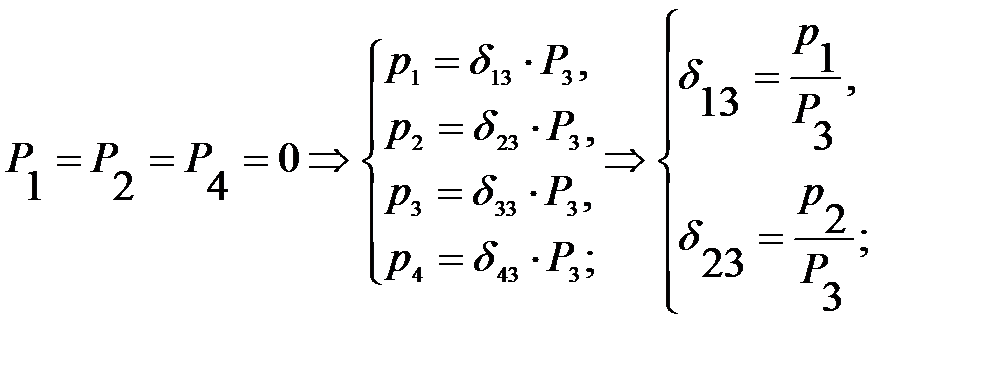
Т. к. у нас несколько значений перемещений и сил, то посчитаем средние коэффициенты матрицы податливости, для чего построим осреднённые линейные зависимости перемещений от нагрузки.
Получили зависимости (II этап):
для точки №1 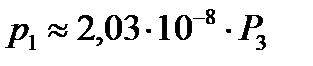 – нагрузка;
– нагрузка;
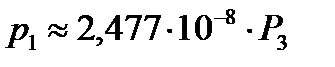 – разгрузка;
– разгрузка;
для точки №2 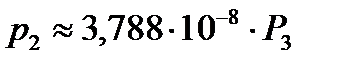 – нагрузка;
– нагрузка;
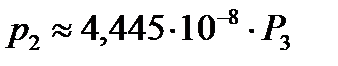 – разгрузка;
– разгрузка;
Т. е. можно принять:
для точки №1 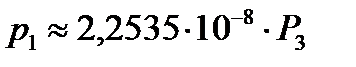 ;
;
для точки №2 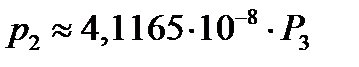 ;
;
Коэффициенты матрицы податливости равны тангенсу углов наклона полученных зависимостей, т. е.:
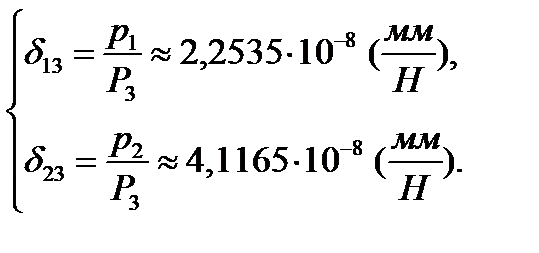
Все коэффициенты матрицы податливости не могут быть определены по результатам данного эксперимента, из-за недостатка данных.
2.6. Напряжения в датчиках.
Исходя из того, что коэффициент пересчета из размерности системы в Па равен 8326, определим напряжения (МПа) в датчиках:
| Нагрузка на 27 узел | ||||||||||||
| Нагрузка | №1 | №2 | №3 | №4 | №5 | №6 | №7 | №8 | №9 | №10 | №11 | №12 |
| 0 | 0,078 | 0,004 | 0,012 | 0,054 | -0,014 | -0,025 | 0,042 | 0,058 | 0,019 | -0,001 | 0,001 | -0,001 |
| 2155 | -12,73 | 0,007 | 5,333 | -0,334 | 0,087 | 0,093 | -0,102 | 0,119 | -0,902 | 0,251 | 0,939 | -0,274 |
| 3755 | -18,883 | -0,132 | 7,872 | -0,492 | 0,098 | 0,126 | -0,113 | 0,213 | -1,361 | 0,387 | 1,414 | -0,455 |
| 5355 | -24,85 | -0,189 | 1,044 | -0,68 | 0,131 | 0,175 | -0,154 | 0,274 | -1,848 | 0,522 | 1,9 | -0,604 |
| 6955 | -30,697 | -0,223 | 13,013 | -0,85 | 0,157 | 0,203 | -0,221 | 0,32 | -2,33 | 0,631 | 2,38 | -0,774 |
| 8555 | -36,19 | -0,31 | 15,534 | -1,046 | 0,252 | 0,247 | -0,28 | 0,38 | -2,803 | 0,76 | 2,84 | -0,94 |
| 10155 | -41,86 | -0,34 | 18,04 | -1,233 | 0,34 | 0,33 | -0,3 | 0,5 | -3,3 | 0,87 | 3,32 | -1,08 |
| 8555 | -37,99 | -0,284 | 16,4 | -1,08 | 0,28 | 0,3 | -0,22 | 0,48 | -2,94 | 0,83 | 3,04 | -0,983 |
| 6955 | -33,07 | -0,29 | 14,17 | -0,89 | 0,22 | 0,25 | -0,15 | 0,46 | -2,52 | 0,723 | 2,63 | -0,88 |
| 5355 | -26,77 | -0,3 | 11,4 | -0,64 | 0,16 | 0,212 | -0,08 | 0,46 | -1,98 | 0,63 | 2,13 | -0,714 |
| 3755 | -20,13 | -0,29 | 8,5 | -0,41 | 0,08 | 0,147 | 0,07 | 0,43 | -1,399 | 0,52 | 1,59 | -0,55 |
| 2155 | -13,03 | -0,26 | 5,44 | -0,165 | 0,008 | 0,084 | 0,21 | 0,413 | -0,803 | 0,4 | -1,05 | -0,383 |
| 0 | 0,173 | -0,24 | -0,19 | 0,32 | -0,15 | -0,019 | 0,411 | 0,394 | 0,246 | 0,148 | 0,025 | -0,114 |
Графики, значения напряжений в зависимости от нагрузки приведены в Приложении 2
| Нагрузка на 15 узел | ||||||||||||
| Нагрузка | №1 | №2 | №3 | №4 | №5 | №6 | №7 | №8 | №9 | №10 | №11 | №12 |
| 0 | 0,173 | -0,24 | -0,19 | 0,32 | -0,15 | -0,019 | 0,411 | 0,394 | 0,246 | 0,148 | 0,025 | -0,114 |
| 2155 | -2,4 | -0,074 | 1,47 | -0,073 | -1,963 | 0,034 | 2,569 | 3,063 | -5,18 | 0,639 | 4,32 | -1,24 |
| 3755 | -3,051 | -0,056 | 1,85 | -0,18 | -2,5 | 0,065 | 3,164 | 3,8 | -6,66 | 0,804 | 5,53 | -1,56 |
| 5355 | -4,2 | -0,028 | 2,47 | -0,34 | -3,27 | 0,097 | 4,123 | 4,973 | -9,12 | 1,02 | 7,47 | -2,12 |
| 6955 | -5,13 | 0,021 | 2,995 | -0,471 | -3,9 | 0,15 | 4,912 | 5,95 | -11,2 | 1,195 | 9,11 | -2,58 |
| 8555 | -5,4 | -0,003 | 3,83 | -0,605 | -4,053 | 0,143 | 5,76 | 7,01 | -13,526 | 1,424 | 10,964 | -3,08 |
| 10155 | -6,57 | 0,003 | 4,214 | -0,792 | -4,79 | 0,166 | 6,53 | 7,97 | -15,58 | 1,64 | 12,62 | -3,51 |
| 8555 | -6,59 | -0,027 | 4,17 | -0,83 | -4,8 | 0,15 | 6,51 | 7,94 | -15,54 | 1,63 | 12,57 | -3,54 |
| 6955 | -6,59 | -0,008 | 4,131 | -0,83 | -4,75 | 0,171 | 6,52 | 7,952 | -15,5 | 1,626 | 12,522 | -3,522 |
| 5355 | -5,721 | -0,072 | 3,65 | -0,68 | -4,15 | 0,13 | 5,78 | 7,014 | -13,62 | 1,45 | 11,024 | -3,12 |
| 3755 | -3,76 | -0,16 | 2,59 | -0,324 | -2,821 | 0,064 | 4,22 | 5,054 | -9,45 | 1,051 | 7,703 | -2,24 |
| 2155 | -2,11 | -0,225 | 1,7 | -0,053 | -1,76 | -0,006 | 2,89 | 3,421 | -5,94 | 0,73 | 4,926 | -1,501 |
| 0 | 0,84 | -0,364 | 0,05 | 0,382 | 0,212 | -0,071 | 0,48 | 0,45 | 0,35 | 0,204 | -0,013 | -0,155 |








