1.4 Занести в таблицу координаты х и у вершины петли (точка А рисунке 1).
1.5 Уменьшая подаваемое напряжение (поворотом ручки потенциометра R на панели кассеты), получить еще 5 петель гистерезиса, измерить и записать в таблицу координаты х и у их вершин.
1.6 Результаты измерений занести в разработанную таблицу.
2 Задание 2. Определение остаточной индукции Dr. и коэрцитивной силы Ес.
2.1 Вновь получить на экране максимальную петлю гистерезиса. Ручками осциллографа ««» и «↕» выставить ее на экране осциллографа симметрично относительно центральных вертикальной и горизонтальной осей и зарисовать в масштабе сетки экрана осциллографа.
2.2 Найти с помощью координатной сетки экрана осциллографа координату пересечения петли с осью ординат yr , соответствующую остаточной индукции, и координату хс, соответствующую коэрцитивной силе сетки.
Обработка результатов измерений
1 По данным таблицы вычислить значения D и E по формулам (8) и (11) соответственно и построить начальную кривую поляризации. Значения параметров b1, b2, h, S, С для расчетов по этим формулам приведены в таблице на рабочем месте.
2 По данным, взятым из построенного графика D= f(E), по формуле (12) рассчитать не менее 10 значений e и построить график зависимости e = f (E).
3 Определить максимальное значение eмах и напряженность поля, при котором оно наблюдается.
4 По значениям уr. и хс рассчитать по формулам (8) и (11) коэрцитивную силу Ес и остаточную индукцию Dr соответственно.
5 Рассчитать погрешность полученных значений коэрцитивной силы и остаточной индукции.
Контрольные вопросы
1 В чем заключается поляризация диэлектриков в электрическом поле?
2 Какие типы поляризации наблюдаются в диэлектриках?
3 Что такое спонтанная поляризация сегнетоэлектриков?
4 Каковы основные свойства сегнетоэлектриков?
5 Как определяются составляющие поляризации сегнетоэлектрика?
6 Что такое остаточная поляризация, остаточная индукция?
7 Что такое коэрцитивная сила?
8 В чем заключается состояние насыщения сегнетоэлектрика?
Лабораторная работа 2.3
ИЗМЕРЕНИЕ СОПРОТИВЛЕНИЯ С ПОМОЩЬЮ МОСТИКА УИТСТОНА
Цель работы
Изучить применение законов Кирхгофа для измерения сопротивлений с помощью мостика Уитстона.
Введение
Измерить любое сопротивление можно на основании закона Ома
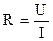. (1)
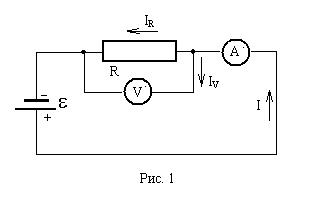
Для этого достаточно собрать простую цепь, чтобы измерить напряжение и ток (рис. 1). Однако, как видно из рисунка амперметр показывает общий, проходящий через неизвестное сопротивление IR и ток через вольтметр IV, т.е. I = IR+ IV.
С учетом этого формула (1) примет вид
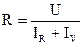. (2)
Из этой формулы видно, что из-за измерительного тока вольтметра амперметр вносит погрешность при определении сопротивления: по формуле (2) получается заниженное значение измеряемого сопротивления. На практике стремятся максимально увеличить сопротивление вольтметра
чтобы уменьшить его измерительный
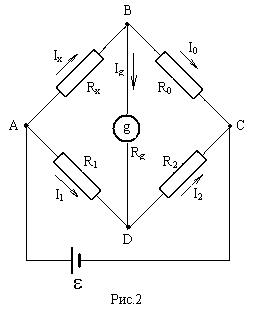ток IV. Но, как бы ни было, измерительный ток всегда существует и принципиально по закону Ома нельзя точно измерить величину неизвестного сопротивления. В связи с этим возникла необходимость разработать такие способы измерения, когда измерительный ток через прибор отсутствовал. Таким способом, например, является метод мостика Уитстона. Мостик представляет собой электрическую цепь из четырех последовательно соединенных сопротивлений Rх, Rо, R1 и R2 (рис.2). По одной диагонали такого четырехполюсника между точками В и Д включен гальванометр. К другой диагонали подключен источник тока e. Особенностью такой схемы является то, что подбором сопротивлений можно добиться такого состояния цепи, когда ток через гальванометр (через «мостик») равен нулю.
Такое состояние цепи можно проанализировать на основе законов Кирхгофа.