Изучение электростатического поля с помощью проводящей бумаги
Государственный университет информационных технологий, механики и оптики.
Лабораторная работа №1
Изучение электростатического поля с помощью проводящей бумаги
студент: Порохня П.Н
группа 1345
преподаватель: Соловьев С.М.
Санкт-Петербург 2011 г.
Цель работы:
1. Экспериментальное определение формы эквипотенциальных поверхностей в моделях плоского и цилиндрического конденсаторов.
2. Расчет напряженности электростатического поля по найденному распределению потенциала.
3. Проверка теоретических предсказаний относительно координатной зависимости потенциала для обеих моделей.
Теоретические основы лабораторной работы:
Взаимодействие между неподвижными электрически заряженными телами осуществляется посредством электрического поля. При этом каждое заряженное тело создает в окружающем пространстве поле, воздействующее на другие заряженные тела, и само это тело испытывает на себе воздействие электрических полей, созданных окружающими телами. Если заряды-
источники неподвижны, то их электрическое поле стационарно, т.е. не изменяется с течением времени. Такое поле называют электростатическим. Силовой характеристикой электрического поля служит вектор его напряженности. Этот вектор в данной точке пространства определяется соотношением:
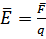 (1)
(1)
где 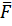 – сила, действующая на неподвижный заряд q, помещенный в данную точку. Заряд q в формуле (1) , с помощью которого детектируется электрическое поле, называется «пробным». Для графического изображения электростатических полей используют силовые линии.
– сила, действующая на неподвижный заряд q, помещенный в данную точку. Заряд q в формуле (1) , с помощью которого детектируется электрическое поле, называется «пробным». Для графического изображения электростатических полей используют силовые линии.
Силовыми линиями (линиями напряженности) называют линии, касательные к которым в каждой точке совпадают с направлением вектора напряженности в этой точке. Силовые линии электростатического поля разомкнуты. Они начинаются на положительных зарядах и оканчиваются на отрицательных зарядах (в частности, они могут уходить в бесконечность или приходить из бесконечности).
Энергетической характеристикой электрического поля является его потенциал. Потенциалом в данной точке поля называется скалярная величина
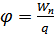 (2)
(2)
где Wп – потенциальная энергия заряда q, помещенного в данную точку. При перемещении заряда q из точки с потенциалом 1 j в точку с потенциалом 2 j силы электростатического поля совершают над зарядом работу
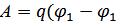 ) (3)
) (3)
Геометрическое место точек, в которых потенциал имеет одинаковую величину, называется эквипотенциальной поверхностью.
Напряженность и потенциал электростатического поля связаны друг с другом соотношениями
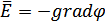 (4)
(4)
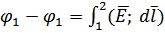 (5)
(5)
Вектор градиента (градиент) потенциала в формуле (4) определяется через частные производные потенциала по декартовым координатам x, y, z :
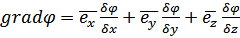 (6)
(6)
Здесь 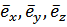 – единичные вектора положительных направлений (орты) координатных осей Ox, Oy, Oz. Направление градиента потенциала в данной точке совпадает с направлением быстрейшего возрастания потенциала, а его величина равна быстроте изменения потенциала на единицу перемещения в этом направлении. Направление вектора
– единичные вектора положительных направлений (орты) координатных осей Ox, Oy, Oz. Направление градиента потенциала в данной точке совпадает с направлением быстрейшего возрастания потенциала, а его величина равна быстроте изменения потенциала на единицу перемещения в этом направлении. Направление вектора 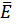 напряженности электростатического поля в соответствии с формулой (4) противоположно направлению градиента. Следовательно, вектор напряженности направлен в сторону наибыстрейшего убывания потенциала. Кроме того, из формулы (5) следует, что вектор
напряженности электростатического поля в соответствии с формулой (4) противоположно направлению градиента. Следовательно, вектор напряженности направлен в сторону наибыстрейшего убывания потенциала. Кроме того, из формулы (5) следует, что вектор 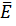 перпендикулярен к эквипотенциальной поверхности в любой ее точке.
перпендикулярен к эквипотенциальной поверхности в любой ее точке.
Если известны потенциалы 1 j и 2 j двух точек, лежащих на одной силовой линии (см. рис.1), то средняя напряженность между этими точками вычисляется по формуле
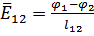 (7)
(7)
где 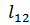 – длина участка силовой линии между точками. Если относительное изменение локального значения напряженности между выбранными точками невелико, то формула (7) дает значение близкое к напряженности на середине участка 1-2.
– длина участка силовой линии между точками. Если относительное изменение локального значения напряженности между выбранными точками невелико, то формула (7) дает значение близкое к напряженности на середине участка 1-2.
Рис.1. АА’– эквипотенциальная поверхность с потенциалом 1 j ,
ВВ’– с потенциалом 2 j ; 1 и 2 – две точки одной силовой линии
В лабораторной работе исследуется пространственно распределение потенциала и напряженности электростатического поля для двух плоских моделей, в одной из которых электростатическое поле совпадает с полем плоского конденсатора (рис. 2а), в другой – с полем цилиндрического конденсатора (рис. 2б). Внутри плоского конденсатора вдали от краев пластин электрическое поле однородно ( E = const), и потенциал равномерно возрастает при движении вдоль координатной оси x от отрицательной обкладки к положительной (рис. 2а) по формуле
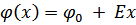 (8)
(8)
Где 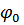 –потенциал отрицательной пластины, E –модуль вектора электрической напряженности.
–потенциал отрицательной пластины, E –модуль вектора электрической напряженности.
Рис.2. Схематическое изображение
поля: а) плоский конденсатор; б)
цилиндрический конденсатор.
Тонкие сплошные линии – линии
напряженности, пунктирные линии
– сечения эквипотенциальных
поверхностей плоскостью рисунка.
Внутри цилиндрического конденсатора модуль электрической напряженности спадает обратно пропорционально расстоянию r от оси (E:1r), и, если внутренняя обкладка заряжена отрицательно (рис. 2б), потенциал изменяется в соответствии с формулой
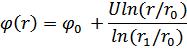
где 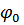 – потенциал внутренней обкладки; U – разность потенциалов между обкладками;
– потенциал внутренней обкладки; U – разность потенциалов между обкладками; 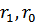 – радиусы внутренней и внешней обкладок соответственно.
– радиусы внутренней и внешней обкладок соответственно.
Состав лабораторной установки:
1. источник постоянного напряжения;
2. цифровой вольтметр;
3. планшеты с моделями плоского и
цилиндрического конденсаторов;
4. миллиметровые линейки;
5. соединительные провода;
6. щуп для измерения электрического
потенциала.
Обработка результатов измерений:
Таблица 1 У=16см
| № точки | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| х,см | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 |
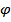 ,В ,В
| 9,1 | 8,4 | 7,5 | 6,5 | 5,5 | 4,6 | 3,6 | 2,7 |
Таблица 2 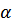 =
= 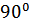
| № точки | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| r, мм | 15 | 18 | 20 | 25 | 30 | 35 | 40 | 50 | 60 | 80 |
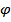 ,В ,В
| 8 | 7 | 6,5 | 5,3 | 4,5 | 3,9 | 3,4 | 2,5 | 1,8 | 0,8 |
По формуле (7) из данных таблицы 1 вычислим среднюю напряженность
электростатического поля между точками 1-2, 3-4, 5-6, 7-8.
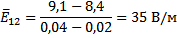
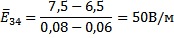
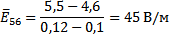
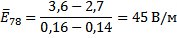
Выведем формулу для расчета погрешности DE и вычислить погрешности для значений, найденных в п. 3.
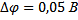
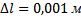
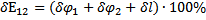
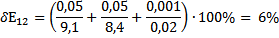
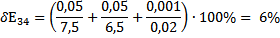
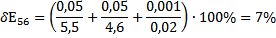
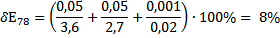
По данным таблицы 1 построим график зависимости 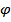 (х ) потенциала от координаты в плоском конденсаторе (нанесём точки и построим аппроксимирующую прямую).
(х ) потенциала от координаты в плоском конденсаторе (нанесём точки и построим аппроксимирующую прямую).
По данным таблицы 2 построить график зависимости 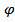 (r) потенциала от координаты в цилиндрическом конденсаторе (нанести точки и построить аппроксимирующую гладкую кривую). Определить графически угловой коэффициент наклона касательной к графику
(r) потенциала от координаты в цилиндрическом конденсаторе (нанести точки и построить аппроксимирующую гладкую кривую). Определить графически угловой коэффициент наклона касательной к графику 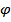 (r) в точках с координатами r = 20; 40; 60; 80 мм. Найденные значения углового коэффициента k, как следует из формулы (4) равны значениям напряженности при заданных r.
(r) в точках с координатами r = 20; 40; 60; 80 мм. Найденные значения углового коэффициента k, как следует из формулы (4) равны значениям напряженности при заданных r.
Выведем формулу для расчета погрешности и вычислить ее для найденных в п. 7. Значений углового коэффициента.
K=tg(80)=(0,8-0)/(99-80)=0,04 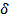 tg(80)=(0,05/0,8+0,001/0,019)
tg(80)=(0,05/0,8+0,001/0,019) 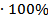 =12
=12 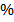
K=tg(60)= (1,8-0)/(89-60)=0,06 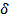 tg(60)=(0,05/1,8+0,001/0,029)
tg(60)=(0,05/1,8+0,001/0,029) 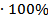 =6
=6 
K=tg(40)= 3,4/(74-40)=0,1 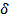 tg(40)=(0,05/3,4+0,001/0,034)
tg(40)=(0,05/3,4+0,001/0,034) 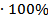 =4
=4 
K=tg(20)=6,5/(47-20)=0,2 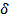 tg(20)=(0,05/6,5+0,001/0,027)
tg(20)=(0,05/6,5+0,001/0,027) 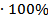 =4
=4 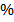
По данным таблицы 2 заполним таблицу 3.
Таблица 3
r0=200мм
| № точки | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
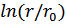
| -2,60 | -2,40 | -2,30 | -2,10 | -1,90 | -1,7 | -1,60 | -1,40 | -1,20 | -0,90 |
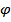 ,В ,В
| 8 | 7 | 6,5 | 5,3 | 4,5 | 3,9 | 3,4 | 2,5 | 1,8 | 0,8 |
По данным таблицы 3 построить график зависимости потенциала от величины
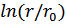 (нанести точки и построить аппроксимирующую прямую). По формуле (9) эта зависимость должна быть прямолинейной.
(нанести точки и построить аппроксимирующую прямую). По формуле (9) эта зависимость должна быть прямолинейной.
Вывод: В ходе определения работы было определены формы эквипотенциальных поверхностей в моделях плоского и цилиндрического конденсаторов; рассчитаны напряженности электростатического поля по распределению потенциала; проверены теоретические предсказания относительно координатной зависимости потенциала для обеих моделей.








