Министерство науки и высшего образования Российской Федерации
Мытищинский филиал федерального государственного бюджетного
образовательного учреждения высшего образования
«Московский государственный технический университет имени Н.Э. Баумана
(национальный исследовательский университет)»
(МФ МГТУ им. Н.Э. Баумана)
ФАКУЛЬТЕТ КОСМИЧЕСКИЙ
КАФЕДРА САУ (К1)
ЛАБОРАТОРНАЯ РАБОТА № 7
| |||||
| |||||
| |||||
Студент________________ _________________ ____________________
(Группа) (Подпись, дата) (И.О. Фамилия)
|
Преподаватель _________________ ____________________
(Подпись, дата) (И.О. Фамилия)
2020 г.
Вариант №6
Цель лабораторной работы.
Определение экстремума нелинейных функций при нелинейных ограничениях методами штрафных функций.
Постановка задачи синтеза оптимальной системы.
Дана задача условной минимизации.
1. Дать аналитическое решение методом внешних штрафных функций.
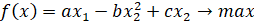
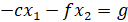
2. Дать аналитическое решение методом штрафных функций двумя способами:
· методом внешних штрафных функций;
· методом внутренних штрафных функций (логарифмическая штрафная функция).
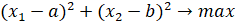
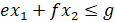
Начальные условия: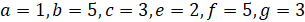 
.
Ход работы.
1. Подставив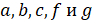 
, получаем следующие выражения.
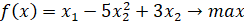
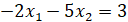
Последнее выражение можно представить следующим образом.
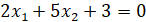
Оно описывает множество Ω.
Решение сводится к задаче безусловной оптимизации.
В методе внешних штрафных функций штрафы 𝛿𝑘(𝑥|Ω), сходящиеся при 𝑘 → ∞ к индикаторной функции, строят так, что при всех k было 𝛿𝑘(𝑥|Ω) = 0 для 𝑥 ∈ Ω и 𝛿𝑘(𝑥|Ω) ≥ 0 для 𝑥 ∉ Ω.
Чаще всего считается, что
𝛿𝑘(𝑥|Ω) = 𝑟𝑘Ф(𝑥).
Здесь Ф(х) – функция, определённая на всем пространстве значений х, равная нулю на множестве Ω и положительная за его пределами.
Теперь стоит перейти к рассматриваемой задаче.
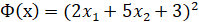
Если Ф(х)=0 при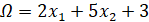 
, то штрафная функция имеет следующий вид.
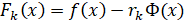
Теперь подставляем известные значения.
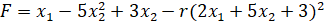
Далее представлено вычисление частных производных.
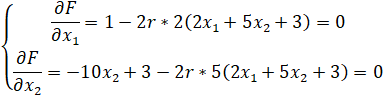
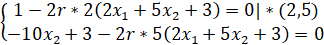
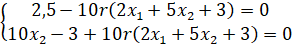
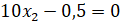
Получим:
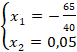
Вычисленные значения х1 и х2 подставляем в выражение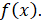 
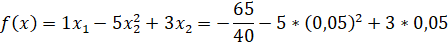
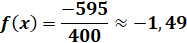
2. Сначала решим методом внешних штрафных функций. Подставив 
, получаем следующие выражения.
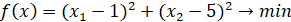
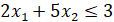
Последнее выражение можно представить следующим образом.
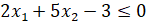
Оно описывает множество Ω.
В методе внешних штрафных функций при построении штрафов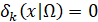 
при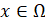 
они сходятся при 
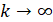к индикаторной функции.
А при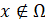 
.
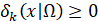Известно, что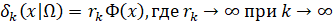 
.
Здесь Ф(х) – функция, определённая на всем пространстве значений х, равная нулю на множестве Ω и положительная за его пределами.
Теперь стоит перейти к рассматриваемой задаче.
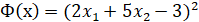
Если Ф(х)=0 при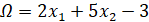 
, то штрафная функция имеет следующий вид.
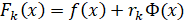
Теперь подставляем известные значения.
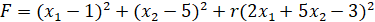
Далее представлено вычисление частных производных.
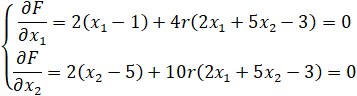
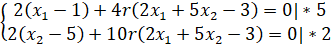
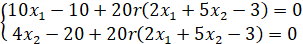
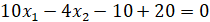
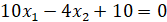
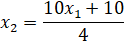
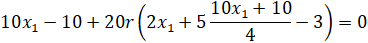
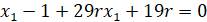
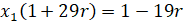
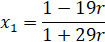
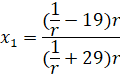
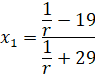
С учётом, что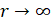 
, далее представлено нахождение 
.
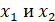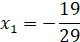
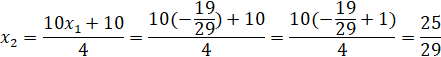
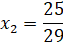
Найденные значения лежат в заданном множестве Ω, поскольку выполняется условие .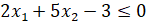
Далее представлен подсчёт значения функции для найденных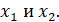 
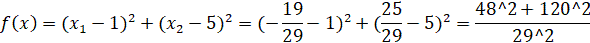
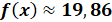
Теперь найдем решение другим способом. Пусть r=0.
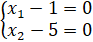
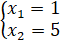
Найденные значения лежат вне заданного множества Ω, поскольку не выполняется условие .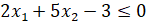
Сейчас нужно перейти к применению метода внутренних штрафных функций с использованием логарифмической штрафной функции.
Известно, что множество Ω представляется следующим выражением.
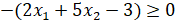
Тогда Ф(х) имеет следующий вид.
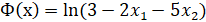
Далее записана штрафная функция.
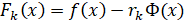
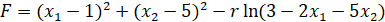
Вычисляются частные производные.
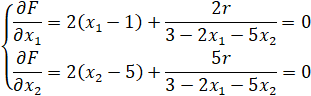
Аналогично первому варианту решения опускаем, что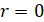 
.
Значит, система приобретает вид, представленный далее.
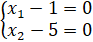
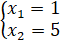
Данные значения не удовлетворяют поставленному условию.
Вывод.
Таким образом, определён экстремум нелинейных функций при нелинейных ограничениях методами штрафных функций.
Найден максимум функции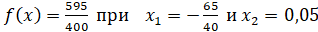 
.
С помощью метода внешних штрафных функций стало известно, что минимум достигается пр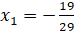и 
и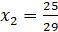 
и он равен 
.
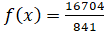Также найдены ещё два значения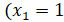 
и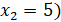 
, однако они не удовлетворяют заданным условиям.