Министерство науки и высшего образования Российской Федерации

Дата: 2025-05-25; Просмотры: 3

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Мытищинский филиал федерального государственного бюджетного
образовательного учреждения высшего образования

«Московский государственный технический университет имени Н.Э. Баумана

(национальный исследовательский университет)»

(МФ МГТУ им. Н.Э. Баумана)

ФАКУЛЬТЕТ КОСМИЧЕСКИЙ

КАФЕДРА САУ (К1)

Лабораторная работа №5

Студент______________ _________________ __________________________

(Группа) (Подпись, дата) (И.О. Фамилия)

Преподаватель _________________ ___________________________

(Подпись, дата) (И.О. Фамилия)

2020 г .

Вариант 6.

Цель лабораторной работы

Аналитический синтез оптимального закона управления линейным объектом с помощью уравнения Эйлера, моделирование на компьютере особенностей динамики системы и выявление влияния изменений коэффициента усиления оптимального регулятора на характер, качество и время переходного процесса системы.

Постановка задачи синтеза оптимальной системы.

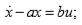
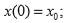
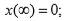
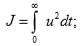
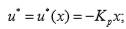
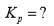
Исходные данные:

а=0.1;

b =0.3.

Решение задачи аналитического синтеза оптимального регулятора и расчет коэффициента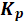

Для начала определим u:

( );

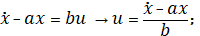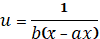Подставляем полученное значение u в функционал :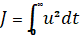

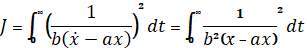
Составим для приведенного функционала уравнение Эйлера:

;

;

;

;

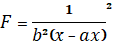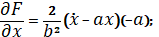
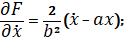
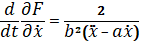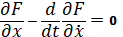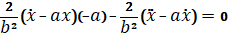Решая уравнение Эйлера и используя уравнение объекта находим:

;

( );

;

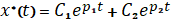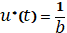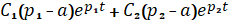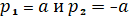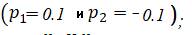
Здесь 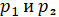корни характеристического уравнения дифференциального уравнения Эйлера.

Используя граничные условия, находим постоянные интегрирования 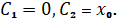Заметим, что значение 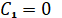вытекает из условия 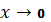при 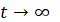которое может выполняться только при равенстве нулю коэффициента при экспоненте, показатель которой имеет положительную вещественную часть.

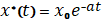и ;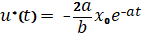

;

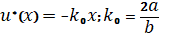В итоге получим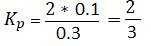

Теперь убедимся, что на найденной экстремали 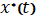выполняется необходимое условие минимума для приведенного функционала:

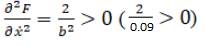
Структурная схема оптимальной системы

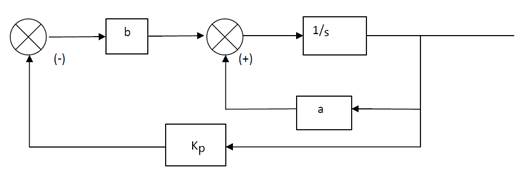
Схема моделирования оптимальной системы