Тема: Логические элементы (И, ИЛИ, НЕ).
ПЛАН ЗАНЯТИЯ
Дисциплина: ОП.02 Архитектура аппаратных средств
Преподаватель: Машарова Р.В.
Курс: 2
Группа: 1ИСП-21
Специальность: Информационные системы и программирование
Дата: 30.09.22
Время проведения: 13.30 – 15.00, 4 пара
Тема: Логические элементы (И, ИЛИ, НЕ).
Цель занятия:
Дидактическая: познакомиться с логическими элементами (И, ИЛИ, НЕ).
Развивающая: развивать логическое и критическое мышление, умение обобщать и синтезировать знания
Вид занятия лекция
Литература:
1. Сенкевич А. В. Архитектура ЭВМ и вычислительные системы : учебник для студ. учреждений сред. проф. образования / А.В.Сенкевич. — М. : Издательский центр «Академия», 2014. — 240 с.
2. Колдаев, В.Л. Архитектура ЭВМ / В.Л. Колдаев, С.А. Лупин. - М.: Форум, Инфра-М, 2009 - 384с.
3. Кузин, А.В. Архитектура ЭВМ и вычислительных систем: учебник/ А.В.Кузин, С.А.Пескова. - М.: Форум: Инфра-М, 2006. - 352с.
4. Максимов, Н.В. Архитектура ЭВМ и вычислительных систем: учебник/ Н.В. Максимов, Т.Л. Партыка, И.И. Попов. - М.: Форум, 2008. - 512с.
Тема: Логические элементы (И, ИЛИ, НЕ).
1. Использование логики в ОТ.
2. Логические элементы: инвертор, коньюнткор, дизьюнктор, триггер.
1. Использование логики в ОТ.
Именно математическая логика с развитием вычислительной техники оказалась в тесной взаимосвязи с вопросами конструирования и программирования на ЭВМ. Алгебра логики
нашла широкое применение изначально при разработке релейно-контактных схем. Первым фундаментальным исследованиям, обратило внимание инженеров, занимавшихся
проектированием ЭВМ, возможность анализа электрических цепей с помощью булевой алгебры была опубликована в декабре 1938 г. ,. статья американца Клода Шеннона «Символический анализ релейно-контактных схем». После этой статьи проектирования ЭВМ не обходилось без применения булевой алгебры. Роль ключа в схемах сначала играли электромеханические реле, затем использовались электронные лампы и, резисторы. Развитие технологии позволило сочетать несколько логических элементов на одной интегральной схеме.
Современный компьютер включает такие базовые понятия, как процессор, память, регистр, и т.д. Оказывается, все они включают в себя базовые логические элементы, которые в свою очередь, и функционируют на законах логики, изученные нами выше. Но давайте все по порядку.
Логическая схема любого самого сложного устройства строится на основе объединения электронных элементов. Эти элементы реализуют конкретные логические операции и носят, название логических элементов.
2. Логические элементы: инвертор, коньюнткор, дизьюнктор, триггер.
Логический элемент - это схема, реализующая логические операции и, или, не.
Любую электрическую схему можно разбить на цепочки или из последовательно параллельно соединенных контактов, которыми мы назовем элементным.
Инвертор реализует операции отрицания, или инверсию. В схемах изображается в следующие способы:
| Х |
|
| F = не X | ||
|
|
|
| не |
|
|
Элемент не. Реализует логическую сделку не.
Х - входной сигнал, F - выходной сигнал. Потому что выходной сигнал всегда противоположный входному, элемент не и получил название «инвентор»
У инвертора один вход и один выход. Сигнал на выходе появляется тогда, когда на входе его и, и наоборот.
Конъюнктор - реализует операции конъюнкции. В схемах изображается следующим образом:
| X | & |
|
|
|
|
| F=X і Y | |
| Y |
|
|
|
|
|
| і |
|
Элемент И. реализует логическую операцию И.
F = X или Y
X, Y - входные сигналы, F - выходной сигнал.
У конъюнктора один выход и не менее двух входов. Сигнал на выходе появляется тогда и только тогда, когда на все входы поданы сигналы.
Дизьюнктор - реализует операцию дизъюнкции. В схемах изображается следующим образом:
| X | 1 |
|
|
|
|
|
| F=X або Y | ||
| Y |
|
|
|
|
|
|
| або |
|
|
Элемент или. Реализует логическую операцию или.
F = X или Y
X, Y - входные сигналы, F - выходной сигнал.
У дизьюнктора один выход и не менее двух входов. Сигнал на выходе появляется тогда и только тогда, когда на все входы не представлены сигналы.
Логические операции реализующих операции И, ИЛИ и НЕ, называются основными логическими элементами, так как с их помощью можно реализовать в виде логической схемы любую логическую функцию.
Реализовать каждую из этих трех базовых структур можно различными электронными устройствами. Для простоты приведем только двумя способами: с помощью контактов реле, и с помощью транзисторов.
На вход схемы подается сигнал Х, а на выходе образуется сигнал НЕ Х.
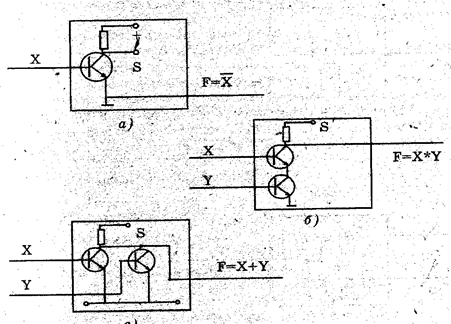
На рис. изображена схема простейшего транзисторного ключа. В управляющей (базовой) цепи включен источник управляющего напряжения Х. Если напряжение Х мало, то
транзистор заперт и ток в цепи очень мал. Согласно напряжение F велико. Если напряжение Х достаточно большая, то транзистор открыт, в цепи протекает ток и напряжение F близко к нулю. Из этого следует, что такой ключ есть схеме инвертирующий есть схеме «НЕ», реализующая операцию отрицания, поскольку увеличение входного напряжения
Х сопровождается уменьшением выходного напряжения Y и, наоборот, уменьшение входного напряжения Х вызывает увеличение выходного напряжения Y. Схема, реализующая операцию отрицания, называется схемой «НЕ» (или инвертором)
Коньюкция двух булевых переменных X и Y реализуется последовательным включением двух нормально разомкнутых контактов реле, соответствующие этим переменным (рис.27б). На выходе рассматриваемой схеме сигнал будет только тогда
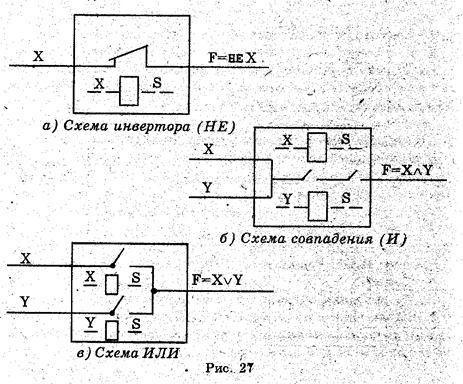
На выходе рассматриваемой схемы сигнал будет только тогда, когда на оба входа Х и Y поступают сигналы (идет ток). Для транзисторного аналога, представлен этот же вариант на рис 28б; Схема, реализующая операцию конъюнкции, называется схемой «И» (или схеме совпадения).
Дизъюнкция двух булевых переменных реализуется параллельным включением нормально разомкнутых контактов реле, соответствующие этим переменным (рис. 27в). На выходе этой схемы сигнал будет тогда, когда он будет представлен, по крайней мере, на один из ее входов (Х и Y). Для транзисторного аналога представлен этот же вариант на рис 28в. Схема, реализующая операцию дизъюнкции, называется схемой «ИЛИ».
Как было уже сказано, логические элементы «И», ИЛИ могут иметь более двух входов, на которые. подаются значения булевых переменных (значения сигналов). Выход у каждого логического элемента один.








