Метод покрытия решений/условий
Критерий покрытия решений/условий требует такого достаточного набора тестов, чтобы все возможные результаты каждого условия выполнялись по крайней мере один раз, все результаты каждого решения выполнялись по крайней мере один раз и, кроме того, каждой точке входа передавалось управление по крайней мере один раз.
Недостатки метода:
· не всегда можно проверить все условия;
· невозможно проверить условия, которые скрыты другими условиями;
· недостаточная чувствительность к ошибкам в логических выражениях.
Так, в рассматриваемом примере два теста метода покрытия условий
a) A=2, B=0, X=4 ace
b) A=1, B=1, X=0 abd
отвечают и критерию покрытия решений/условий. Это является следствием того, что одни условия приведенных решений скрывают другие условия в этих решениях. Так, если условие
А > 1 будет ложным, транслятор может не проверять условия 5=0, поскольку при любом результате условия В=0 результат решения ((А> 1)&(В=0)) примет значение ложь. То есть в варианте на рис. 1 не все результаты всех условий выполнятся в процессе тестирования.
Рассмотрим реализацию того же примера на рис. 2. Наиболее полное покрытие тестами в этом случае осуществляется
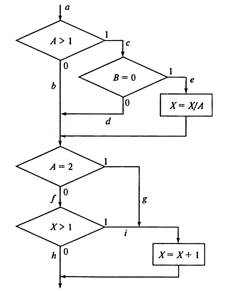
Рис. 2. Пример алгоритма программы
так, чтобы выполнялись все возможные результаты каждого простого решения. Для этого нужно покрыть пути aceg (тест А = 2, В=0, Х=4), acdfh (тест A = 3, В = 1, Х=0), abfh (тест А = О, В = 0, Х= 0), abfi (тест А = 0, В = 0, Х= 2).
Протестировав алгоритм на рис. 2, нетрудно убедиться в том, что критерии покрытия условий и критерии покрытия решений/условий недостаточно чувствительны к ошибкам в логических выражениях.
Метод комбинаторного покрытия условий
Критерий комбинаторного покрытия условий удовлетворяет также и критериям покрытия решений, покрытия условий и покрытия решений/условий.
Этот метод требует создания такого числа тестов, чтобы все возможные комбинации результатов условия в каждом решении выполнялись по крайней мере один раз. По этому критерию в рассматриваемом примере должны быть покрыты тестами следующие восемь комбинаций:
1. A>1, B=0.
2. A>1, B≠0.
3. A≤1, B≠0.
4. A≤1, B=0.
5. A=2, X>1.
6. A=2, X≤1.
7. A≠2, X>1.
8. A≠2, X≤1
Для того чтобы протестировать эти комбинации, необязательно использовать все 8 тестов. Фактически они могут быть покрыты четырьмя тестами (табл. 4):
• А = 2, В= 0, Х= 4 {покрывает I, 5};
• А = 2, В= 1, Х- 1 {покрывает 2, 6};
• А = 0,5, В=0, Х= 2 {покрывает 3, 7};
• А = 1, В= 0, Х= 1 {покрывает 4, 8}.
Таблица 4 - Результаты тестирования методом комбинаторного покрытия условий

Порядок выполнения работы
1. Спроектировать тесты по принципу «белого ящика» для программы, разработанной в лабораторной работе № 4. Использовать схемы алгоритмов, разработанные и уточненные в лабораторных работах № 2, 3.
2. Выбрать несколько алгоритмов для тестирования и обозначить буквами или цифрами ветви этих алгоритмов.
3. Выписать пути алгоритма, которые должны быть проверены тестами для выбранного метода тестирования.
4. Записать тесты, которые позволят пройти по путям алгоритма.
5. Протестировать разработанную вами программу. Результаты оформить в виде таблиц (см. табл. Л5.1—Л5.4).
6. Проверить все виды тестов и сделать выводы об их эффективности.
7. Оформить отчет по лабораторной работе.
8. Сдать и защитить работу.
Защита отчета по лабораторной работе
Отчет по лабораторной работе должен состоять из:
1. Постановки задачи.
2. Блок-схемы программ.
3. Тестов.
4. Таблиц тестирования программы.
5. Выводов по результатам тестирования (не забывайте, что целью тестирования является обнаружение ошибок в программе).
Контрольные вопросы
1. Охарактеризуйте этап реализации и тестирования программного продукта.
2. Какие существуют виды тестирования?
3. Назовите критерии выбора тестов.
4. Перечислите свойства тестов.
5. Приведите критерии надежности программ.
6. В чем заключается оценка надежности программ?








