Метод покрытия операторов
Целью этого метода тестирования является выполнение каждого оператора программы хотя бы один раз.
Пример.
Если для тестирования задать значения переменных А = 2, В=0, Х=3, будет реализован путь асе, т. е. каждый оператор программы выполнится один раз (рис. 1, а). Но если внести в алгоритм ошибки — заменить в первом условии and на or, а во втором Х> 1 на Х< 1 (рис. 1, б), ни одна ошибка не будет обнаружена (табл. 1). Кроме того, путь abd вообще не будет охвачен тестом, и если в нем есть ошибка, она также не будет обнаружена. В табл. 1 ожидаемый результат определяется по блок-схеме на рис. 1, а; а фактический — по рис. 1, б.
Как видно из этой таблицы, ни одна из внесенных в алгоритм ошибок не будет обнаружена.
Таблица 1 - Результат тестирования методом покрытия операторов

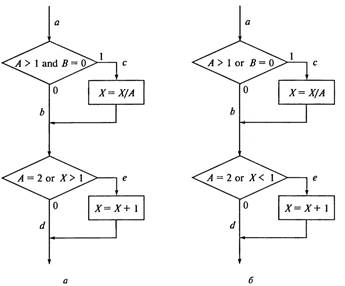
Рис. 1. Пример алгоритма программы:
а — правильный; б — с ошибкой
Метод покрытия решений (покрытия переходов)
Согласно методу покрытия решений каждое направление перехода должно быть реализовано, по крайней мере, один раз. Этот метод включает в себя критерий покрытия операторов, так как при выполнении всех направлений переходов выполнятся все операторы, находящиеся на этих направлениях.
Для программы, приведенной на рис. 1, покрытие решений может быть выполнено двумя тестами, покрывающими пути {асе, abd), либо {acd, abe). Для этого выберем следующие исходные данные: {А = 3, В = 0, Х=Ъ) — в первом случае и {А = 2, В= 1, Х= 1} — во втором. Однако путь, где Хне меняется, будет проверен с вероятностью 50 %: если во втором условии вместо условия Х> 1 записано Х< 1, то ошибка не будет обнаружена двумя тестами.
Результаты тестирования приведены в табл. 2.
Таблица 2 - Результат тестирования методом покрытия решений

Метод покрытия условий
Этот метод может дать лучшие результаты по сравнению с предыдущими. В соответствии с методом покрытия условий записывается число тестов, достаточное для того, чтобы все возможные результаты каждого условия в решении выполнялись, по крайней мере, один раз.
В рассматриваемом примере имеем четыре условия: {А>1,
В=0}, {А = 2, Х> 1}. Следовательно, требуется достаточное число тестов, такое, чтобы реализовать ситуации, где А > 1, А ≤ 1, В= 0 и В≠0 в точке а и А = 2, А ≠ 2, Х> 1 и Х≤ 1 в точке b. Тесты, удовлетворяющие критерию покрытия условий (табл. 3), и соответствующие им пути:
a) A=2, B=0, X=4 ace;
b) A=1, B=1, X=0 abd
Таблица 3. Результаты тестирования методом покрытия условий









