Балтийский государственный технический университет
Министерство образования и науки РФ
БАЛТИЙСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
“ВОЕНМЕХ” им. Д.Ф. Устинова
Кафедра ракетостроение
Отчет по лабораторной работе №2
Компьютерное обеспечение технических решений
Выполнил: Сафиулин Р.Т.
Вариант № 9
Группа: КВ-61
Проверил: Степанов М.М.
Лабораторная работа №2
Численное решение уравнения масс
летательного аппарата (ЛА).
> restart;
Digits := 5;
Методические указания.
Цель и содержание работы.
Цель- ознакомление с итерационными методами решения уравнений на примере решения уравнения масс ЛА методом последовательных приближений.
Содержание работы:
Рассматривается задача определения стартовой массы ЛА m0 в зависимости от проектных переменных. Подобные задачи решаются на этапе баллистического проектирования ЛА.
Основным путем повышения точности расчета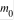 
является т.н. путь декомпозиции массы, согласно которому 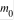представляет собой сумму масс соответствующих структурно - функциональных элементов ЛА 
.
.
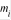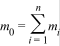В лабораторной работе приняты следующие обозначения:
f- уравнение масс летательного аппарата;
m_p- масса полезной нагрузки;
m_pl- масса конструкции планера ЛА;
m_jet- масса двигательной установки;
m_fuel- масса топлива;
m_0- стартовая масса ЛА;
Остальные обозначения вводятся по мере необходимости.
Порядок выполнения лабораторной работы:
- присвоить переменным m_p, k_pl, alpha и mu значения в соответствии с полученным заданием;
- задать точность расчета для решения уравнения масс epsilon (0,01 ... 0,0001);
- произвести расчеты путем выбора пункта Edit \ Execute \ Worksheet главного меню среды Maple 13.
В ходе лабораторной работы требуется исследовать:
- условия сходимости метода последовательны итераций;
- зависимость числа итераций, требующихся для обеспечения заданной точности расчетов, от значений точности;
- влияние числа значащих цифр, определяемого константой Digits на относительную погрешность расчетов delta при одинаковой точности расчетов epsilon.
Уравнение масс.
> f := m_p + m_pl + m_jet + m_fuel;
> m_pl := k_pl*m0;
m_jet := alpha*mu*m0;
m_fuel := mu*m0;
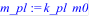
> f;
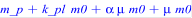
> collect(f,m0);
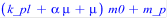
Исходные данные.
Масса полезной нагрузки m _ p.
> m_p := 135;
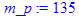
Коэффициент (относительная масса) планера ЛА k _ pl.
> k_pl := 0.35;
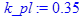
Коэффициент качества двигателя alpha.
> alpha := 0.52;
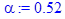
Относительная масса топлива mu.
> mu := 0.33;
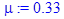
Решение уравнения масс ЛА.
Точность расчетов epsilon.
> epsilon := 0.0001;
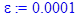
Максимальное допустимое число итераций i _ max.
> i_max := 100;
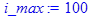
Первое (начальное) приближение:
> x[1] := 100;
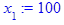
Второе приближение:
> x [2] := eval ( f , m 0 = x [1]);
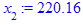
Итерационная процедура:
> for i from 3 while (abs((x[i-1] - x[i-2])
/x[i-2]) > epsilon
and i <= i_max) do
x[i] := eval(f, m0=x[i-1]):
end do;
if i <= i_max then
m0_approx := x[i-1]:
print(" Стартовая масса m0 = ",m0_approx):
print (" Число итераций ", i -1):
else
print (" Число итераций превысило допустимое"):
end if:
| 
| 
| 
|
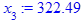
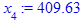
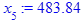
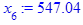
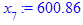
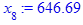
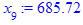
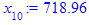
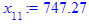
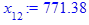
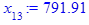
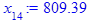
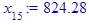
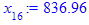
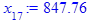
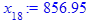
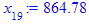
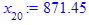
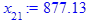
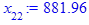
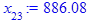
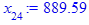
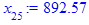
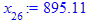
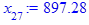
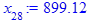
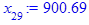
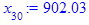
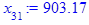
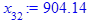
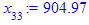
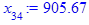
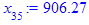
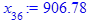
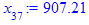
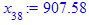
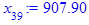
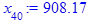
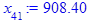
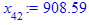
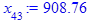
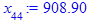
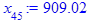
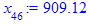
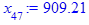
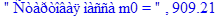
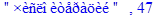
Точное решение уравнения масс.
> f ;
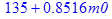
> eqn := f = m0;
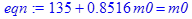
> m0 := solve(eqn,m0);
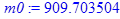
Сравнение результатов.
Относительная ошибка delta.
> delta := 2*abs(m0 - m0_approx)/(m0 + m0_approx);
Вывод:
В данной лабораторной работе мы исследовали условия сходимости метода последовательности итераций, также поняли, что при увеличении точности рассчитав epsilon, число итерации, требующихся для обеспечения заданной точности, уменьшаться.
К тому же разобрались как влияет число значащих цифр, определяемое const Digits на относительную погрешность расчетов delta при одинаковой точности расчетов epsilon: чем больше значащих цифр, тем больше относительная погрешность.