Индивидуальное Домашнее Задание №1
«Косвенные измерения»
Выборочный метод
Цель работы: Научиться правильно высчитывать погрешность косвенных измерений выборочным методом.
Ход Работы
Вычислить погрешность косвенных измерений и записать результат с погрешностью cилы тока в медном проводе диаметром d равной I. Число Авогадро 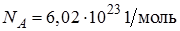 , плотность меди
, плотность меди 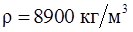 , молярная масса 64 (г/моль). Определить скорость направленного движения электронов:
, молярная масса 64 (г/моль). Определить скорость направленного движения электронов: 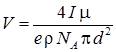 .
.
| N | 1 | 2 | 3 | 4 | 5 | |
| d, мм | 2,02 | 2,01 | 1,98 | 2,03 | 2,02 | qd =0,005 мм |
| I, А | 15,2 | 15,0 | 15,1 | 15,4 | 15,3 | qI =0,05 А |
| V, м/с | 6.97 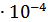
| 6.95 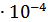
| 7.21 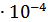
| 6.99 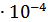
| 7.02 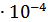
| |
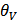
| 0,0058 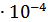
| 0,0569 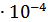
| 0,0566 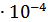
| 0,0572 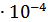
|
1. Находим для каждого наблюдения значение Vi и заносим в таблицу.
Вычисляем результат измерения
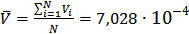 (м/с)
(м/с)
2. СКО наблюдения
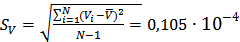 (м/с)
(м/с)
 Рассчитаем размах выборки.
Рассчитаем размах выборки.
R = Vmax – Vmin = 7.21. 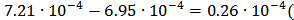 м/c)
м/c)
4. Проверка на промахи
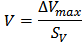
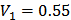 <1.67=
<1.67= 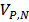
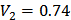 <1.67=
<1.67= 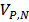
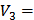 1.73>1.67=
1.73>1.67= 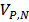 , промах
, промах
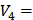 0.36<1.67=
0.36<1.67= 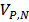
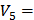 0.08<1.67=
0.08<1.67= 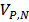
5. СКО наблюдения
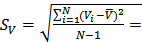 0.06
0.06 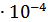 (м/с)
(м/с)
6. СКО измерения
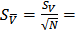 0.035
0.035 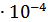 (м/с)
(м/с)
7. Доверительная граница случайной погрешности
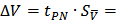 0.098
0.098 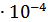 (м/с)
(м/с)
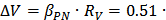 0.26
0.26 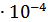 = 0,133
= 0,133 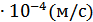
8. Граница приборной погрешности
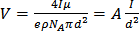 ;
; 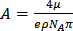 ;
;
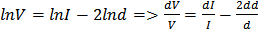 ;
;
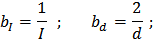
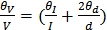 ;
;
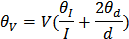
Полученные результаты для 5 случаев заносим в таблицу
9. Среднее значение приборной погрешности
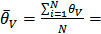 0,057
0,057 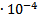
10. Полная погрешность результата измерения ускорения свободного падения.
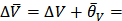 0,133
0,133 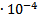 +0,057
+0,057 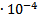 = 0,19
= 0,19 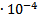 (м/с)
(м/с)
11. Окончательный результат:
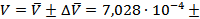 0,19
0,19 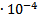 (м/с)
(м/с)
Вывод: В ходе работы с данными из таблицы были получены средние значения каждой из величин и значения абсолютных погрешностей, которые были использованы для нахождения среднего значения функции, а так же ее полной погрешности.








