«Косвенные измерения»
Метод переноса погрешностей
Описание способа: Данный метод используется в случае, когда каждая из величин x, y, z , представляющих собой аргументы функции, измеряется независимо от остальных в своей серии опытов, и эти величины образуют выборки (близки друг к другу). Число опытов в сериях, вообще говоря, не обязано быть одинаковым, требуется только неизменность условий для прямо измеряемой величины в своей серии, неизменность условий для f во всех сериях и взаимная независимость всех опытов.
Цель работы: Научиться правильно высчитывать погрешность косвенных измерений методом переноса погрешностей.
Ход Работы
Вычислить погрешность косвенных измерений и записать результат с погрешностью плотности материала дробинки, где m- масса, d –диаметр, E= 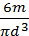
| d, мм | 1,52 | 1,48 | 1,54 | 1,51 | 1,53 | qd =0,005 мм |
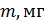
| 21 | 20 | 21 | 19 | 22 | qm =0,5 мг |
1. По формулам прямых измерений определить величины 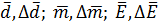 (с учётом приборных погрешностей).
(с учётом приборных погрешностей).
а) Определяем среднее выборочное значение 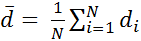 =
=
= 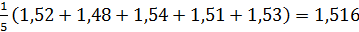
б) Рассчитаем выборочное СКО среднего.
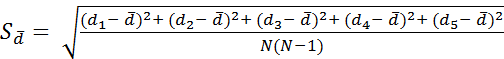 =
=
= 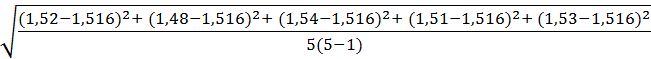
= 0,01
в) Оценка погрешности по Стьюденту.
При N = 5, p = 95%, то tp , N = 2,8.
Δ d = tp , N * 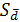 = 2,8 * 0,01 = 0,028
= 2,8 * 0,01 = 0,028
г) Найдём полную погрешность результата измерений.
Θ d = 0,005 мм
Δ 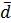 =
= 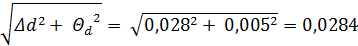 (мм)
(мм)
а) Определяем среднее выборочное значение 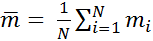 =
=
= 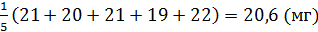
б) Рассчитаем выборочное СКО среднего.
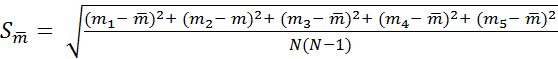 =
=
= 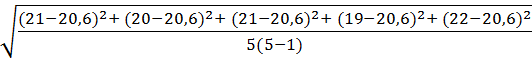 =
=
=0,51 .
в) Оценка погрешности по Стьюденту.
При N = 5, p = 95%, то tp , N = 2,8.
Δ 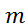 = tp , N *
= tp , N * 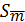 = 2,8 * 0,51 = 1,428(мг)
= 2,8 * 0,51 = 1,428(мг)
г) Найдём полную погрешность результата измерений.
Θ 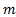 = 0,5 мг
= 0,5 мг
Δ 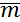 =
= 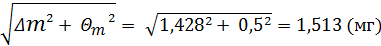
2. Рассчитать значение функции 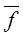 = f(
= f( 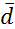 ,
, 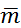 ).
).
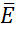 =
= 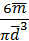 =
= 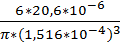 =11,3*
=11,3* 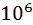
3.Вычислить частные производные от функции
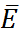 =
= 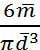
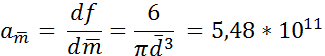
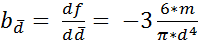 =-2,24*
=-2,24* 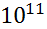
4. Вычислить полную погрешность функции
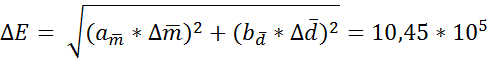
5. Записать результат измерения и округлить его.
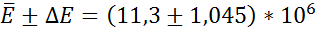
6. Сводим результаты обработки эксперимента в таблицу 2.
| Таблица 2. | ||||||||||||||||||||
| d, мм | 1.52 | 1.48 | 1.54 | 1.51 | 1.53 | q d =0,005 мм | ||||||||||||||
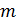 , мг , мг
| 21 | 20 | 21 | 19 | 22 | q | ||||||||||||||
| d↑i | 1.48 | 1.51 | 1.52 | 1.53 | 1,54 |
R d =d↑N– d↑ 1 = 0,06 | ||||||||||||||
| di+1-di | 0.03 | 0.01 | 0.01 | 0.01 | UP,N Rd =0.06 | |||||||||||||||
D di = di – 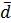
| -0,036 | -0,006 | 0,004 | 0,014 | 0.024 | SD mi = 0 | ||||||||||||||
| (D di )2 | 12,96* | 36* | 16* | 1,96* | 5,76* | S(D mi )2=21,2* | ||||||||||||||
|
| ||||||||||||||||||||
| m↑i | 19 | 20 | 21 | 21 | 22 | 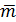 =20,6,
Rm=m↑N–m↑ 1 =3 =20,6,
Rm=m↑N–m↑ 1 =3
| ||||||||||||||
| mi+1-mi | 1 | 1 | 0 | 1 | UP,N R 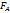 =0.2* =0.2* 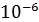
| |||||||||||||||
| D m = | -1,6 | -0,6 | 0,4 | 0,4 | 1,4 | SD 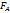 i =0 i =0
| ||||||||||||||
| (D mi)2 | 2,56 | 0,36 | 0,16 | 0,16 | 1,96 | S(D mi )2 =5,2 | ||||||||||||||
|
| ||||||||||||||||||||
|
| ||||||||||||||||||||
| E = | ||||||||||||||||||||
Вывод: В ходе работы с данными из таблицы были получены средние значения каждой из величин и значения абсолютных погрешностей, которые были использованы для нахождения среднего значения функции, а так же ее полной погрешности.









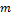 =0,5 мг
=0,5 мг 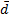 =1,516
=1,516 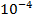
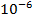
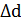 = 0.028 ,
= 0.028 ,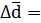 0.0284 , d= 1,516
0.0284 , d= 1,516 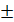 0.028 P=95% N=5
0.028 P=95% N=5 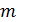 i –
i – 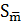 = 0,51*
= 0,51* 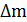 = 1,43*
= 1,43* 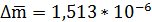 , m=(20,6
, m=(20,6 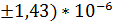 P=95% N=5
P=95% N=5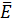 = 11,3*
= 11,3* 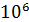 ,
, 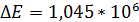
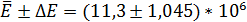 P =95% N =5
P =95% N =5