Оптимальный режим тренировки элемента КСНО определяется временем испытания этого элемента , после которого вероятность безотказной работы элемента в течение заданного времени t максимальна.

Дата: 2025-06-14; Просмотры: 6
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

Если обозначить через 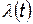интенсивность отказов элемента после тренировки, то средняя интенсивность отказов в течение времени t будет

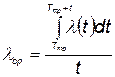. (5.75)

Для определения минимальной 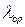приравняем производну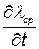ю нулю:

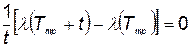. (5.76)

Это уравнение позволяет определить 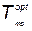, если известен вид функции .

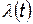При определении 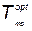мы воспользовались тем обстоятельством, что при минимальной средней интенсивности отказов вероятность безотказной работы максимальна. Если необходимо найти оптимальное время тренировки, минимизирующее суммарные затраты, то поступают следующим образом.

Пусть стоимость одного элемента КСНО равна 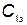, стоимость единицы времени тренировки 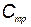и ущерб от отказа элемента 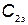. Всего в КСНО используется N элементов.

Количество не отказавших за время тренировок элементов должно быть равно N элементам, используемым в КСНО:

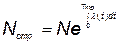, (5.77)

где 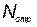— количество элементов, поставленных на тренировку.

После тренировки не откажет 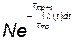элементов, а откажет соответственно

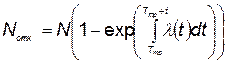. (5.78)

 

Определим суммарные затраты, которые включают в себя:

а) стоимость элементов, поставленных на тренировку:

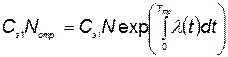; (5.79)

б) стоимость тренировки

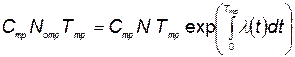; (5.80)

(здесь предполагается, что отказавшие элементы с испытаний не снимаются до конца тренировки);

в) ущерб от отказа элементов:

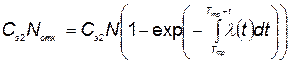, (5.81)

т. е.

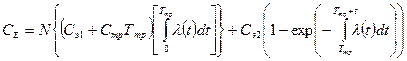. (5.82)

Для определения оптимального времени тренировки 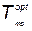необходимо от 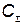взять производную по 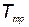и приравнять нулю:

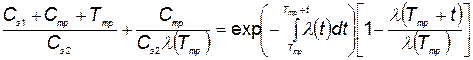. (5.83)

Решение этого уравнения удобно проводить графически, для чего строятся графики правой и левой частей уравнения как функции от 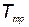и находится точка пересечения.

 

5.4.3. Определение оптимального времени замены элементов КСНО

Повысить надежность КСНО можно заменой элементов КСНО, отработавших определенный ресурс времени .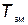

При большом времени работы элемента до его замены 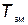(профилактическая замена) увеличивается интенсивность отказов, при малом времени увеличиваются затраты, связанные с заменой этих элементов.

Если затраты, связанные с профилактической заменой элемента, равны 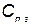, а затраты при отказе элемента во время работы 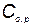то средняя стоимость замены элементов за время 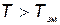будет

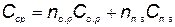, (5.84)

где 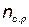и 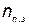— число отказавшихся во время работы и замененных в профилактических целях элементов. Соответственно эти величины определяются по формулам

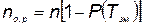; (5.85)

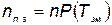, (5.86)

где 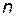— среднее число замененных элементов

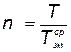; (5.87)

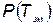— вероятность безотказной работы элемента за время 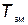; 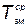— средний срок службы элемента при условии профилактических замен.

Подставив 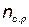, 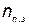и 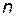в выражение для средних затрат, будем иметь

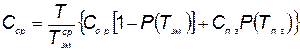. (5.88)

Это выражение можно записать иначе, если учесть, что 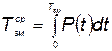, и разделить обе части на 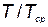, где 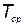— средний срок службы элемента при отсутствии профилактических замен:

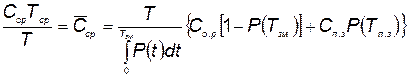. (5.89)

Задача определения оптимального времени замены элементов КСНО сводится к выбору такого 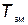, при котором удельные средние затраты 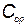, определяемые по формуле (5.88), минимальны.

Следует отметить, что для экспоненциального распределения времени службы элементов их профилактическая замена целесообразна, поскольку функция 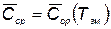монотонно убывает и не имеет минимума.

5.4.4. Выбор оптимального распределения надежности отдельных элементов КСНО

Обычно стоимость отдельного элемента КСНО может быть представлена в виде зависимости

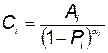, (5.90)

где 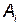и 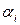; — коэффициенты, позволяющие статистические данные аппроксимировать кривой; 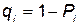— вероятность отказа i-го элемента.

Вероятность безотказной работы КСНО при отсутствии резервирования может быть определена по формуле (для случая малых значений)

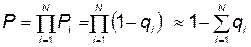. (5.91)

Отсюда

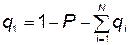. (5.92)

Суммарная стоимость КСНО складывается из стоимостей отдельных элементов:

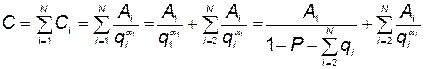. (5.93)

Следует выбрать вероятность отказа i-го элемента 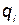таким образом, чтобы суммарная стоимость КСНО была минимальной. Для этого необходимым условием является равенство нулю всех частных производных от С по :

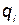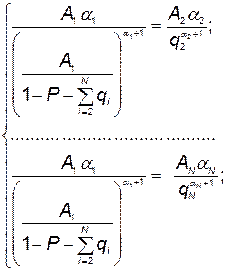(5.94)

т. е.

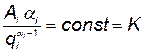. (5.95)

 

Из (5.95) имеем

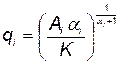. (5.96)

Подставив 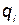вычисленное по формуле (5.96), в формулу (5.91), будем иметь

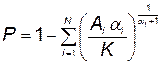. (5.97)

Откуда при 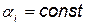можно определить

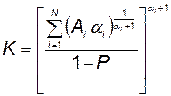. (5.98)

Выражение (5.96) с учетом (5.98) можно записать

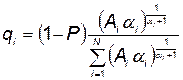. (5.99)

Полученная зависимость дает возможность найти оптимальное распределение надежности отдельных элементов при заданной надежности всего КСНО (или агрегата КСНО), а также совместно с уравнением (5.93) позволяет найти зависимость 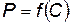при оптимальном распределении надежности отдельных элементов. Имея зависимость 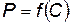и пользуясь методикой для выбора оптимальной надежности КСНО или его агрегатов, изложенной выше, можно определить оптимальную надежность всего КСНО.

Следует отметить, что выбор оптимального режима тренировок элементов КСНО, а также оптимального времени замены этих элементов может производиться независимо от выбора общей надежности всего комплекса или его отдельного агрегата.

5.4.5. Определение оптимального числа резервных элементов КСНО

Как указывалось выше, одним из эффективных методов повышения надежности КСНО является резервирование его элементов. В свою очередь, увеличение количества элементов приводит к увеличению весовых характеристик и габаритных размеров, а также стоимости всего КСНО.

Если надежность всего КСНО задана, то при наличии резервирования вероятность безотказной работы будет

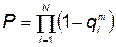, (5.100)

где 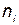— количество i - x элементов повышающих надежность за счет резервирования; 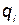— вероятность отказа i-го элемента; 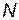- общее количество разнотипных элементов (дублирующие элементы не входят).

Определение оптимального числа резервных элементов 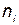заключается в выборе такого вектора 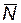(с компонентами 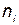), который минимизирует суммарную стоимость КСНО.

Суммарная стоимость КСНО может быть представлена следующей зависимостью:

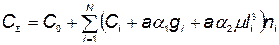, (5.101)

где 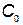— постоянная составляющая затрат, не зависящая от резервирования; 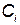, а — статистические коэффициенты; 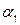, 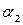— коэффициенты, учитывающие увеличение массы 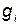и размеров 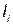за счет введения дополнительных элементов; 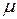— коэффициент, учитывающий увеличение объема за счет размеров .

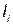При определении оптимального количества резервных элементов следует учитывать возможность существования ограничений по массе и габаритам, которые для данного случая могут быть представлены в следующем виде:

;

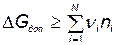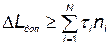; (5.102)

где ; .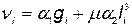

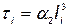Поставленная задача формулируется так: необходимо выбрать вектор 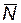с компонентами 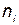таким образом, чтобы при соблюдении условия (5.100) и ограничений (5.102) минимизировать 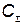, определяемую по формуле (5.101).

В общем случае эта задача нелинейного целочисленного программирования, которая при больших значениях может быть решена либо методом полного перебора, либо наискорейшего спуска, либо другими численными методами с применением ЭВМ.

В простейшем случае, когда 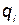малы и отсутствуют ограничения по массе и габаритам, поставленная задача может быть решена аналитически.

Для этого случая можно записать приближенное уравнение, получаемое из (5.100):

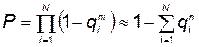. (5.103)

Уравнение (5.101) перепишем в виде

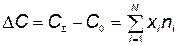, (5.104)

где .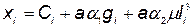

Оптимизацию будем проводить методом неопределенных множителей Лагранжа, для чего составим функцию

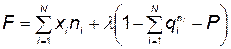(5.105)

и, приравняв производные по 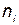и к нулю, получим

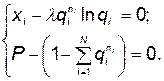(5.106)

Решение этой системы уравнений позволяет найти оптимальное значение

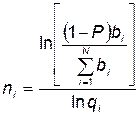, (5.107)

где .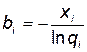

Вместо натуральных логарифмов в приближенных расчетах можно пользоваться десятичными.