5.3. Выбор оптимальных сроков службы КСНО и его элементов
5.3.1. Постановка обобщенной задачи замены КСНО
При создании КСНО одним из важных является вопрос о целесообразности разработки нового комплекса или его элементов взамен существующего. Решение такой задачи дает ответ на начальной стадии проектирования на вопрос, стоит ли начинать разработку нового КСНО или каких-то его элементов или целесообразнее воспользоваться существующим комплексом.
Поскольку вновь созданные технические устройства более эффективны, чем старые, но требуют больших затрат на разработку и производство, то, очевидно, существуют оптимальные сроки разработки КСНО (или элементов) новых типов.
Сформировать такую задачу можно следующим образом. Определить оптимальные сроки разработки нового КСНО и замены им старого при условии, что показатель эффективности КСНО (например, суммарные затраты на заданный период) будет минимальным и в любой момент будет обеспечено необходимое качество работы, которую необходимо выполнить данному КСНО. Считается, что сразу же после разработки новый комплекс поступает в производство, а производство комплекса старого типа прекращается. Кроме того, разработка нового КСНО начинается тогда, когда до конца рассматриваемого периода ее можно завершить.
Математически эта задача формулируется следующим образом.
Определить совокупность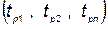 
, включая число разработок n , при которой с учетом условия
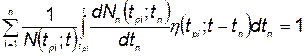(5.43)
обеспечивается минимум суммарных затрат на комплексы всех типов с учетом приведения затрат к единому моменту времени:
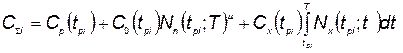(5.44)
или
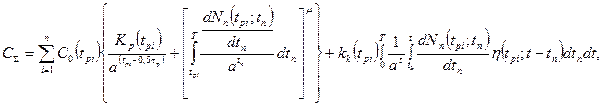(5.45)
где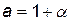 
; 
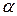— коэффициент эффективности капиталовложений; 
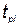— время конца разработки КСНО нового типа (i-гo типа); 
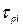— время, затрачиваемое на разработку 1-го нового комплекса; 
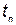— время производства нового комплекса; 
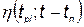— функция живучести, характеризующая процесс хранения и эксплуатации; N ni — количество произведенных комплексов i-го типа; 
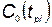и 
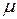— коэффициенты; 
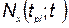— количество устройств j '-ro типа, разработка которого закончена к моменту ; 
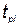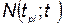— функция потребности в устройстве i-го типа; t — текущее время; 
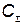— суммарные затраты, которые складываются из затрат на разработку комплексов всех типов, на производство, хранение и эксплуатацию; 
; 
; 
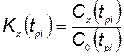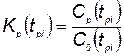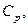
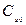— затраты на разработку и хранение соответственно; 
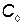— коэффициент. Следует отметить, что рассмотренный процесс не является марковским, поскольку затраты на данный год зависят от предыстории, т. е. от времени производства нового комплекса. В связи с этим для решения подобной задачи метод динамического программирования не может быть использован.
Рассмотрим несколько частных случаев решения поставленной задачи.
5.3.2. Выбор оптимальных сроков службы элемента КСНО для частного случая
Рассмотрим случай:
1) живучесть комплекса задана функцией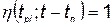 
, т. е. выходом элементов комплекса из строя по мере хранения и эксплуатации можно пренебречь; 2) функция потребности описывается выражением вида
; 
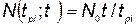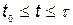, (5.46)
где N0 — коэффициент; t — текущее время; 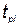— время конца разработки комплекса или элемента КСНО i-го типа;
2) стоимость производства КСНО не зависит от размера партии и времени его разработки, а стоимость разработки КСНО не зависит от времени конца разработки, т.е. функция суммарных затрат описывается выражением
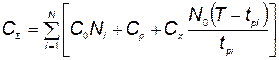. (5.47)
Если рассматривать первую разработку, то уравнение (5.47) запишется в следующем виде:
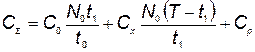. (5.48)
Возьмем производную по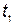 
и приравняем ее нулю:
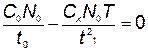. (5.49)
Откуда оптимальное значение
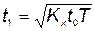, (5.50)
где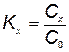 
; 
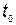— принятый момент начала отсчета; 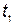— время
конца первой разработки;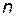 
— количество новых разработок.
Подставляя 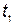, определяемое по формуле (5.50), в выражение суммарной стоимости (5.47), получаем выражение минимальных суммарных затрат, складывающихся из затрат на разработку, их производство, хранение и эксплуатацию:
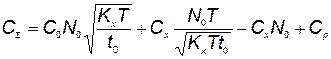. (5.51)
Аналогичным образом решается задача при второй, третьей и других разработках.
Если всего есть 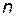новых разработок, то формулы (5.50) и (5.51) принимают соответственно вид
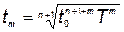, (5.52)
где т — номер разработки,
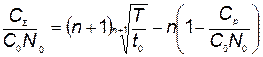. (5.53)
Обозначив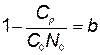 
и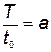 
, а также продифференцировав (5.53) по 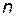и приравняв производную нулю, получим
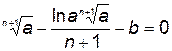. (5.54)
В результате решения этого уравнения находится оптимальная величина 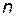. Это уравнение может быть решено графически (рис. 5.2), если задаваться значениями 
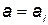и строить график 
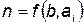по уравнению (5.54).
Поскольку 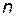может быть только положительной и иметь только целые значения, то значения, полученные с помощью графика, следует округлять в большую и меньшую стороны до целого числа и рассчитывать суммарные затраты для этих двух значений, выбирая из них то при котором 
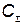будет наименьшим.
Следует отметить, что замена комплекса (или его элементов) с большим сроком живучести целесообразна при большом выигрыше в эффективности нового КСНО по сравнению с комплексом старого типа, т. е. моральное старение комплекса с большим сроком живучести происходит медленнее, чем комплекса с малыми сроками живучести.
5.3.3. Определение рационального срока службы элемента КСНО
В общем случае задача выбора оптимальных сроков службы элементов может быть решена одним из методов численного программирования, например методом случайного поиска, который не гарантирует отыскания точного решения, но в тех случаях, когда мы не располагаем достаточным машинным временем для организации полного перебора, он оказывается полезным.
Рассмотрим частную задачу определения рационального срока службы элемента КСНО, исходя из минимума средних ежегодных затрат за все время эксплуатации. С такой задачей часто приходится встречаться при проектировании нового комплекса, чтобы основные узлы и агрегаты рассчитывать именно на этот срок.
Различают три срока службы технического устройства КСНО:
— физический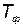 
, по достижении которого устройство к эксплуатации непригодно и ремонту не подлежит;
— экономический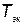 
, обеспечивающий минимальные затраты на эксплуатацию, включая и затраты на приобретение;
- рациональный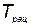 
, учитывающий помимо экономичности реальные возможности государства по обновлению элементов КСНО и занимающий промежуточное положение между 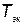и .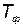
При проектировании следует стремиться к тому, чтобы физический срок службы совпадал с рациональным, поскольку увеличение физического срока службы влечет за собой увеличение стоимости элемента КСНО.
Годовая стоимость эксплуатации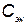 
элемента КСНО может быть представлена в виде следующей зависимости:
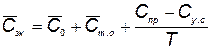, (5.55)
где 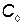— годовые расходы, не зависящие от срока службы (заработная плата обслуживающего персонала и т. п.); 
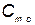— годовые расходы на техническое обслуживание и ремонт; 
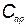— стоимость приобретения элемента КСНО; 
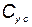— стоимость, возвращаемая при сдаче элемента КСНО в утиль; Т — срок службы.
Годовые расходы на техническое обслуживание и ремонт являются функцией времени эксплуатации. Вид этой функции аналогичен функции интенсивности отказов (см. рис. 5.7). Для практических целей можно пользоваться линейной аппроксимацией этой зависимости, поскольку экономический срок службы выбирается на линейном участке, т. е.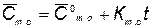 
.
Средние годовые затраты на техническое обслуживание и ремонт за весь срок службы будут, очевидно,
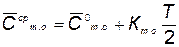, (5.56)
а средняя годовая стоимость эксплуатации элемента КСНО с учетом зависимостей (5.55) и (5.56) определится по формуле
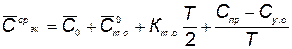. (5.57)
С течением времени производство элемента КСНО становится дешевле, а поэтому уменьшается и стоимость приобретения. Это уменьшение обычно подчиняется закону
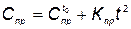, (5.58)
где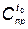 
— стоимость приобретения к начальному периоду времени; 
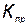— статистический коэффициент.
Уменьшение стоимости приобретения, которое за время Т составит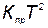 
, приводит к увеличению средних годовых затрат на эксплуатацию:
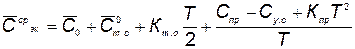. (5.59)
Для определения экономического срока службы элемента КСНО необходимо взять производную от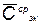 
по T и приравнять ее нулю. После преобразований будем иметь
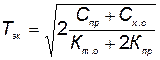. (5.60)
Определив экономический срок службы и исходя из потребностей данного элемента КСНО, выбирают рациональный срок службы.
Необходимое количество произведенных элементов КСНО за время t с учетом необходимости замены вышедших по срокам эксплуатации определяется по формуле
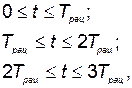
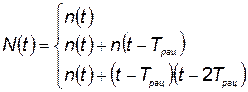при
при
при
(5.61)
где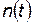 
— ежегодная потребность в элементах КСНО.
5.4. Выбор оптимальной надежности КСНО и его элементов
5.4.1. Общая постановка задачи оптимизации надежности КСНО
Повышение надежности КСНО снижает расходы, связанные эксплуатацией, а также уменьшает потребность в резервировании КСНО или его элементов. С другой стороны, для создания НО с большей надежностью требуются дополнительные затраты, связанные с его разработкой и производством. Эти затраты могут быть существенными. Поэтому, очевидно, существует оптимальная надежность КСНО, определяемая из условия минимизации затрат на выполнение поставленных перед комплексом задач.
Общая задача выбора оптимальной надежности КСНО и путей ее обеспечения может быть сформулирована следующим образом.
Требуется выбрать такие проектные параметры КСНО
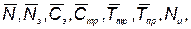(5.62)
при которых суммарные затраты минимизируются, т. е.
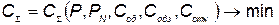, (5.63)
при выполнении дисциплинирующих условий, связывающих стоимость и надежность с проектными параметрами
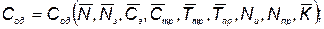
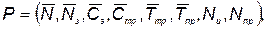(5.64)
и ограничений по массе и габаритам
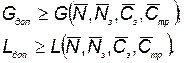(5.65)
Здесь приняты следующие обозначения: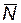 
— вектор с компонентами 
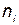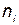; — количество i-х элементов, повышающих надежность за счет резервирования; 
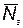— вектор с компонентами 
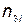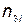; — количество запасных элементов, замена которых происходит достаточно быстро; 
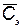— вектор стоимости элементов; 
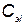— стоимость i –го элемента; 
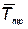— вектор с компонентами 
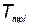, где 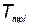— время тренировки i–го элемента; 
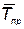— вектор с компонентами 
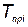, где 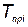— время работы
i–го элемента до замены в процессе профилактических работ; Nи — число испытаний КСНО в процессе отработки;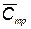 
— вектор с компонентами 
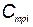, где 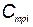— стоимость поддержания температурного режима i -го элемента; Р — надежность КСНО; 
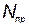— общее количество произведенных КСНО; 
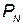- вероятность выполнения поставленной задачи при использовании 
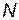комплексов, которая определяется по формуле 
; 
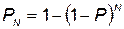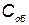— затраты на однократное применение КСНО; 
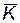— вектор коэффициентов связывающих стоимость с техническими характеристиками КСНО; 
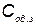— затраты на содержание одного резервного КСНО; 
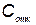— дополнительные затраты, связанные с отказом комплекса.
В зависимости от особенностей функционирования КСНО могут быть наложены ограничения на его массу (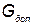 
) и габаритные размеры ( 
).
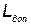Рассмотрим выбор оптимальной надежности на простейшем примере. Пусть в КСНО присутствует агрегат, стоимость приобретения которого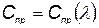 
, где 
— интенсивность отказов. Будем считать, что время отказов имеет экспоненциальное распределение. Стоимость одного часа эксплуатации агрегата, независимо от того, ремонтируется он или работает,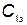 
.
Требуется определить оптимальную надежность агрегата, если стоимость приобретения агрегата определяется по формуле
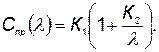(5.66)
Поскольку время отказов имеет экспоненциальное распределение, то вероятность безотказной работы за время Т будет
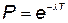, (5.67)
причем среднее время между отказами
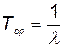, (5.68)
а среднее число отказов за время Т
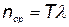. (5.69)
Полезное время работы агрегата за время Т будет
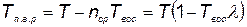, (5.70)
где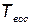 
— среднее время восстановления одного отказа.
Суммарные затраты на один час работы агрегата будут
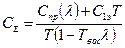. (5.71)
Подставив вместо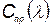 
его значение из (5.66), будем иметь
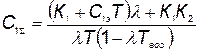. (5.72)
Для выбора оптимальной надежности (вероятности безотказной работы) необходимо найти такое , которое обращает функцию затрат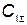 
в минимум, а затем полученное значение 
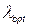подставить в формулу (5.67).
Взяв производную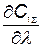 
и приравняв ее нулю, найдем оптимальное значение
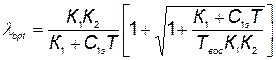. (5.73)
Подставляя значение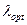 
из (5.73) в (5.67), получаем оптимальное значение вероятности безотказной работы агрегата:
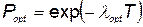. (5.74)
5.4.2. Определение оптимального режима тренировок элементов КСНО
Надежность КСНО характеризуется вероятностью безотказной работы, которая, в свою очередь, складывается из вероятностей безотказной работы составляющих элементов КСНО Очевидно, выбор оптимальных характеристик этих элементов обеспечивает оптимальность всего комплекса в целом.
Одним из путей повышения надежности элемента является его испытания в течение определенного времени с последующей постановкой на агрегат КСНО тех элементов, которые не отказали за время этих испытаний.