Вероятность нахождения комплекса в каком-либо из состояний (А, В, С, D) обозначим PA ( t ), PB ( t ), Pc ( t ), PD ( t ). Составим уравнения, описывающие этот процесс.

Дата: 2025-06-14; Просмотры: 7

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Если вероятность нахождения комплекса в состоянии А была P_A ( t ), то в момент времени ( t + Δ t ) вероятность нахождения комплекса в состоянии A P_A ( t + Δ t ) будет определяться следующим образом:

а) вероятность того, что в момент t комплекс находился в состоянии А и за время Δ t не перешел ни в какое другое состояние, будет

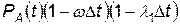; (4.47)

б) вероятность того, что в момент времени t комплекс находился в состоянии B и за время Δt перешел в состояние А, определяется выражением

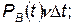(4.48)

в) вероятность того, что в момент времени t комплекс находился в состоянии D и за время Δt перешел в состояние А, находится так:

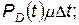(4.49)

г) вероятность перехода комплекса из состояния С в состояние А равна нулю.

Поскольку вероятность того, что за малый промежуток времени произойдет больше одного события, пренебрежимо мала (поток событий ординарный), то вероятность нахождения комплекса в момент времени ( t + Δt ) в состоянии А определяется по теореме сложения вероятностей:

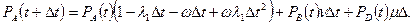(4.50)

Отбрасывая величины второго порядка малости и деля на Δt, а также учитывая, что 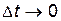, получаем

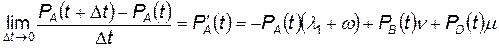. (4.51)

Аналогично получаются уравнения для других состояний:

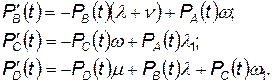(4.52)

Для нахождения коэффициента готовности достаточно иметь стационарное решение, т. е. найти предельные вероятности состояний при достаточно большом t. Так как при 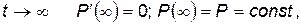то стационарная система уравнений имеет вид

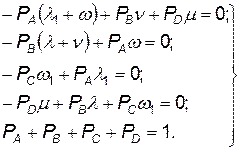(4.53)

Последнее уравнение необходимо добавить потому, что вероятности Р_А, Р _B ,, Р _C , и, P_D составляют полную систему событий. Решая эту систему, получаем

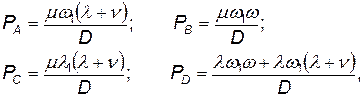(4.54)

где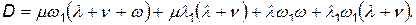

Вероятность исправного состояния комплекса систем наземного обеспечения в произвольный момент времени (коэффициент готовности) определяется формулой К_Г = Р_А+Р _B:

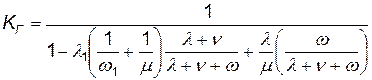. (4.55)

Возможны некоторые частные случаи:

а) случай, когда по условию эксплуатации можно пренебречь интенсивностью или вероятностью возникновения неисправностей в нерабочий период, т.е. пребывания комплекса в состоянии С невозможно, тогда 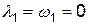и

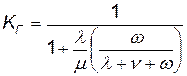; (4.56)

б) случай нерабочего периода, когда для выявления неисправностей проводятся кратковременные проверки, не связанные с наработкой комплекса, т. е. состояние В отсутствует, тогда 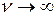и

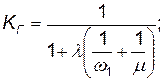(4.57)

в) случай характерен для комплексов, находящихся длительное время в рабочем состоянии, и готовность в этом случае

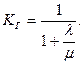(4.58)

Оценка вероятности поражения КСНО. При проектировании КСНО необходимо учитывать возможность его поражения от взрыва. В зависимости от расположения элементов КСНО на ТП и СП, а также от мощности возможного взрыва или серии взрывов вероятность поражения КСНО целесообразно определять либо с учетом эффекта накопления ущерба, либо без учета этого эффекта.

Эффект накопления ущерба необходимо учитывать для крупномасштабных КСНО, когда возможный взрыв ЛА на пусковом устройстве, а также взрывы отдельных объектов СП или ТП не приводят к полному выводу из строя всего комплекса, а поражение происходит по мере накопления ущерба, т. е. вывода со строя все большего количества элементов КСНО. В зависимости от “живучести” отдельных элементов КСНО может быть вычислен условный закон поражения G ( m ) всего комплекса. Зная закон поражения, можно, используя формулу Колмогорова, определить вероятность поражения КСНО, имеющего N взрывоопасных объектов:

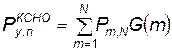, (4.59)

где Р_{т, N}, — вероятность того, что из N возможных взрывов произойдет ровно m (из N взрывоопасных объектов взорвется ровно m). При условии, что взрывы отдельных объектов происходят независимо друг от друга, эта вероятность будет

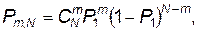(4.60)

где 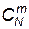— число сочетаний из N по т; Р₁ , — вероятность появления одного взрыва на ТП или СП.

Если системы наземного обеспечения располагаются на относительно небольшой территории и любой единичный взрыв приводит к выводу из строя всего КСНО, вероятность поражения комплекса, имеющего N взрывоопасных элементов:

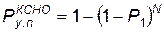. (4.61)

Взрыв на ТП или СП может произойти либо в связи с аварийной ситуацией (взрыв ЛА на ПУ, пожар в хранилище компонентов топлива или в зоне, где проводятся работы с пиротехническими устройствами), либо в результате нанесения удара противником.

Уменьшение вероятности появления аварийной ситуации в процессе подготовки ЛА к пуску обеспечивается соблюдением правил техники безопасности при проведении работ с взрывоопасными компонентами, а также высокой квалификацией обслуживающего персонала, работающего в специальных помещениях на соответствующем оборудовании.

При нанесении удара противником вероятность появления взрыва на ТП или СП определяется как условная вероятность попадания на территорию расположения элементов КСНО боевого заряда. Если действительную поверхность расположения наземного комплекса аппропксимировать равновеликим прямоугольником со сторонами L _X и L_Y, то эта вероятность выражается с помощью табличной функции Лапласа

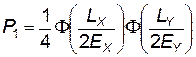, (4.62)

где Е _X , Е _Y — вероятные отклонения в направлении главных осей рассеивания О _x и О _y. Функция Лапласа есть выражение вида

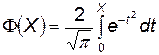. (4.63)

При определении условной вероятности поражения КСНО зарядами большой мощности часто КСНО может рассматриваться как ”точечный” объект, поскольку его линейный размер (например, диаметр равновеликого круга) не больше 0,2 радиуса поражения взрыва.

Вероятность поражения такого малоразмерного объекта определяется, как вероятность его накрытия зоной сплошного поражения, размеры которой определяются мощностью и местом взрыва, а также элементов КСНО и точкой возможного взрыва. Обычно ошибки пусков ЛА подчиняются нормальному закону распределения и рассеивание считается круговым. В этом случае условная вероятность поражения (для кругового ступенчатого закона поражения 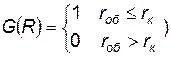равна вероятности попадания в круг радиусом r_k, равным радусу сплошного поражения от действия взрыва:

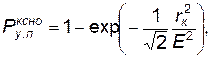(4.64)

где Е — круговое вероятное отклонение.

Радиус зоны сплошного поражения r _к определяется как максимальное горизонтальное удаление цели от эпицентра взрыва, на котором объект может быть безусловно поражен действием ударной волны. Считаем, что

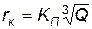, (4.65)

где К_п — коэффициент “живучести” объекта, зависящий от минимального избыточного давления, приводящего к разрушению объекта; Q — тротиловый эквивалент возможного взрыва.

Анализ известных зависимостей показывает, что избыточное давление во фронте ударной волны Δр (единица измерения — бар), создаваемое при наземном взрыве на расстоянии r км от точки взрыва тротиловым эквивалентом в Q Мт, может быть определено, в частности, по следующей эмпирической формуле:

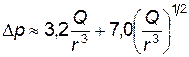. (4.66)

Из этой формулы в результате решения квадратного уравнения относительно т будем иметь

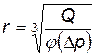, (4.67)

где .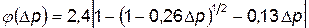

Подставляя в эту формулу минимальное избыточное давление Δр _min , приводящее к разрушению объекта, получаем радиус зоны сплошного поражения

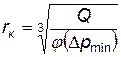, (4.68)

где 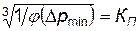— коэффициент “живучести” объекта.

Тогда условная вероятность поражения КСНО (4.64) будет определяться как

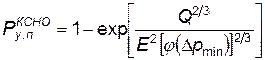. (4.69)

При условии, что производится N независимых пусков, условная вероятность поражения КСНО будет

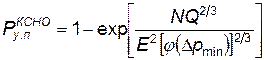. (4.70)

Из четырех величин, входящих в зависимость (4.70), три (N , Q и E) представляют собой характеристики ЛА и головных частей и одна Δр _min — характеристику степени защищенности КСНО от воздействия ударной волны.

Анализ зависимостей (4.69) и (4.70) показывает, что наземный взрыв, целью которого является поражение защищенного КСНО, например ШПУ, будет наиболее действенным при условии, что точность попадания очень высока, т. е. взрыв произойдет в непосредственной близости. Для современных ШПУ максимально допустимое избыточное давление составляет около 7,0 МПа, а для сверхзащищенных ШПУ эта величина доведена до 42,0 МПа.

Следовательно, зона существенного поражения ШПУ от наземного взрыва ограничена размерами образовавшейся воронки и навала грунта, выброшенного на поверхность из этой воронки.

Радиус воронки при наземном взрыве зависит в основном от мощности заряда и свойств грунта и определяется по формуле

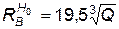, (4.71)

где 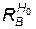— радиус видимой воронки (при наземном взрыве), м; Q — мощность заряда, кт.

Глубина образовавшейся воронки будет составлять

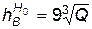, (4.72)

где 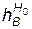— глубина воронки, м; Q — мощность заряда, кт.

Радиус воронки при взрыве зависит как от мощности заряда, так и от глубины, на которой он произошел.

Получена эмпирическая зависимость между радиусом видимой воронки, глубиной взрыва и мощностью:

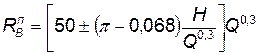, (4.73)

где 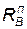— радиус видимой воронки, м; Н — глубина подрыва, м; Q — мощность, кт; знак «-» берется до оптимальной глубины взрыва, а на больших глубинах берется «+».

Из этой формулы видно, что максимальный радиус видимой воронки будет определяться по формуле

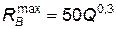, (4.74)

полученной из зависимости (4.73) при условии, что выражение в круглых скобках равно нулю:

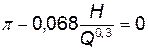. (4.75)

Выражение (4.75) позволяет определить оптимальную глубину взрыва, т. е. глубину, на которой необходимо взорвать заряд, чтобы получить максимальный радиус видимой воронки:

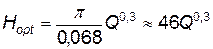, (4.76)

где Н _opt,— глубина, м; Q — мощность, кт.

Для определения минимальной глубины взрыва, когда радиус видимой воронки равен нулю, т. е. когда на поверхности нет воронки (камуфлетный взрыв), воспользуемся формулой (4.73) (со знаком «+»), положив 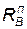= 0.

Имеем

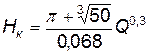. (4.77)

Таким образом, для поражения сильно защищенных ШПУ целесообразно подрыв заряда производить не на поверхности земли, а на оптимальной глубине, определяемой по формуле (4.76).

Сравним вероятности выживания ШПУ при условии, что круговые вероятностные отклонения равны, радиус зоны сплошного поражения ограничен радиусом видимой воронки для наземного взрыва и взрыва на оптимальной глубине.

Для наземного взрыва условная вероятность поражения ШПУ

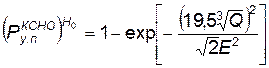. (4.78)

Для взрыва на оптимальной глубине эта величина определяется по формуле

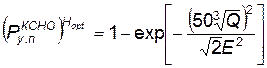. (4.79)

Вероятность “выживания” — это величина, противоположная условной вероятности поражения ШПУ (q =1- P). Для наземного взрыва она будет

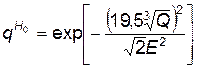, (4.80)

а для взрыва боевой части на оптимальной глубине

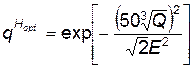. (4.81)

Возьмем отношение этих величин:

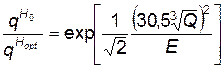. (4.82)

Это отношение показывает, во сколько раз вероятность “выживания” ШПУ при взрыве заряда на оптимальной глубине меньше, чем вероятность “выживания” такой же ШПУ при взрыве заряда на поверхности грунта. Например, для случая взрыва заряда в 1 кт, при значении кругового вероятного отклонения Е = 19,5 м, это отношение будет равно е, т. е. в 2,71 раза вероятность выживания при наземном взрыве больше, чем при взрыве на оптимальной глубине.

4.3.2. Вероятность нормального функционирования элементов КСНО

Вероятность нормального функционирования элементов КСНО при выполнении поставленной задачи определяется вероятностью двух факторов:

— надежностью КСНО, определяемой вероятностью безотказной работы его элементов;

— эффективностью действия КСНО при выполнении поставленной задачи, т. е.

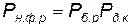(4.83)

где Р_б.р — вероятность безотказной работы элементов КСНО; Р_д.к—вероятность выполнения поставленной задачи при действии КСНО (вероятность действия КСНО).

Вероятность безотказной работы элементов КСНО. Все элементы можно условно разделить на две группы:

— элементы, обслуживающие все стартовые позиции;

— элементы, обслуживающие каждую позицию индивидуально.

В соответствии с таким делением важнейшей характеристикой КСНО является количество каналов для выполнения поставленной задачи перед КСНО и ЛА.

Если комплекс включает один канал по выполняемой работе и n каналов по ЛА, то элементы 1, 2, 3,..., N _{б. p} составляют общую часть комплекса по каналу выполняемой задачи, а элементы 1, 2, 3, …, N _ЛА входят в каждый канал по ЛА.

Если элементы канала по выполняемой задаче соединены последовательно, то вероятность их нормального функционирования определяется по теореме умножения вероятностей независимых событий:

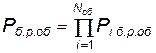, (4.84)

где Р_б.р.об — вероятность нормальной работы 1-го элемента по каналу выполняемой работы.

В этом случае выход из строя одного элемента по каналу выполняемой задачи приводит к срыву работы всего комплекса в целом.

В случае последовательного соединения элементов по каналу ЛА вероятность нормального функционирования j-го канала будет

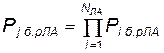, (4.85)

где Р _{i б.рЛА} — вероятность нормальной работы i-го элемента по j-му каналу ЛА.

Вероятность нормальной работы n-канальной системы по ЛА, т. е. вероятность нормального функционирования не менее m каналов по ЛА из n, определяется выражением

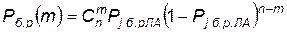, (4.86)

где 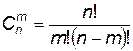— число сочетаний из n элементов по m.

Если комплекс включает один канал по выполняемой задаче и n каналов по ЛА, то вероятность выполнения поставленной задачи всем комплексом ЛА (n-ЛА) с учетом вероятности нормального функционирования КСНО определяется по формуле

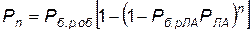, (4.87)

где Р_б.р.об — вероятность нормальной работы по каналу выполняемой задачи;

Р_б.рЛА — вероятность нормальной работы по одному каналу ЛА (в этом случае Р_б.рЛА для всех каналов по ЛА одинакова);

Р_ЛА — вероятность действия ЛА при условии нормальной работы КСНО;

n — число ЛА, использованных в операции.

Из анализа формулы видно, что отказ в работе элементов по каналу решаемой задачи влияет на эффективность всех ЛА в целом, а отказ в работе элементов по каналу ЛА влияет только на эффективность одного ЛА.

Надежность работы элементов (Р_б.р), входящих как в канал по решаемой задаче, так и в каналы по ЛА, определяется опытным путем на основе статистических данных, накопленных в процессе эксплуатации. Обычно =const и

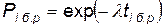, (4.88)

где — интенсивность отказов, определяемая опытным путем;

t _{i б.р} — продолжительность работы i-го элемента.

Количественными показателями надежности являются:

— вероятность безотказной работы;

— частота отказов;

— интенсивность отказов;

— среднее время безотказной работы.

Вероятность безотказной работы — это вероятность того, что в пределах заданного промежутка времени t и заданных условиях работы отказ не произойдет. Она определяется как

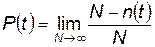, (4.89)

где N — число элементов, подвергнутых испытаниям; n(t) — число вышедших из строя элементов к моменту времени t .

Иногда пользуются понятием “вероятность отказа”:

Q ( t )=1- P ( t ). (4.90)

Плотность распределения времени безотказной работы определяется производной по времени от вероятности отказа:

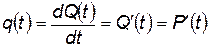. (4.91)

Если имеется кривая распределения безотказной работы по времени (рис. 4.6), то, задаваясь уровнем надежности, легко определить время работы Т, в течение которого надежность изделия будет приемлемой.

Частота отказов α ( t ) представляет собой отношение числа отказавших изделий в единицу времени к общему числу изделий, взятых для испытания:

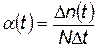, (4.92)

где 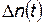— число отказавшихся изделий за время Δ t.

Частота отказов равна плотности распределения времени безотказной работы;

α ( t ) = Q '( t ). (4.93)

Интенсивность отказов 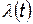— это отношение числа отказавшихся изделий в единицу времени к среднему числу изделий, продолжающих исправно работать при условии, что отказавшие изделия не восстанавливаются и не заменяются:

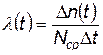, (4.94)

где .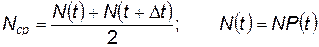

Интенсивность отказов — это условная плотность вероятности возникновения отказа невосстанавливаемого объекта, определяемая для рассматриваемого момента времени при условии, что до этого момента отказ не возник:

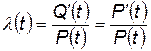. (4.95)

После интегрирования получаем

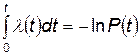
или

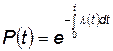. (4.96)

Зависимость интенсивности отказов от времени эксплуатации показана на рис. 4.7, где I — период приработки; II — период нормальной работы; III — период старения.

Первый участок кривой обычно аппроксимируется выражением вида

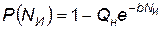, (4.97)

где N _И — количество испытанных образцов; Q _н — начальный уровень

отказа, Q _Н =1-Р_н; b — статистический коэффициент, характеризующий градиент роста уровня надежности.

На втором участке, где интенсивность постоянна, т. е. 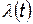= const, вероятность безотказной работы

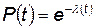. (4.98)

На третьем участке статистика показывает, что вероятность безотказной работы описывается зависимостью

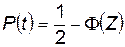, (4.99)

где Ф (Z) — интеграл вероятности:

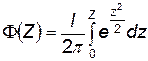; (4.100)

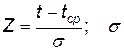— среднеквадратическое отклонение времени безотказной работы от его среднего значения; t_cp — среднее время безотказной работы.

Среднее время безотказной работы — это математическое ожидание безотказной работы:

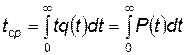. (4.101)

4.3.3. Оценка вероятности поражения обслуживающего персонала при аварийном подрыве ЛА

При проектировании стартовых комплексов для ЛА одним из важных вопросов является обеспечение безопасности обслуживающего персонала в аварийной ситуации, которая оценивается вероятностью несчастных или смертельных случаев при подрыве ЛА вблизи точки старта.

Если после запуска на ЛА возникает аварийная ситуация, т.е. значения каких-то параметров превышают допустимые, то специальная служба с помощью радиоуправляемых бортовых детонаторов поджигает удлиненные заряды системы аварийного подрыва, которые осуществляют разрыв корпуса ЛА. В результате этого давление в камере сгорания падает и заканчивается активный участок полета.

Поскольку мощность зарядов аварийного подрыва мала, то детонация топлива при срабатывании этих зарядов невозможна. Однако, хотя ЛА и не детонирует, но он разваливается на множество обломков, среди которых имеются большие куски, в том числе и горящие, и, следовательно, имеется реальная опасность поражения горящими обломками. Эта опасность особенно велика в начальный период полета, когда большая часть топлива еще не сгорела. На более поздней стадии полета топлива остается меньше, а горящие куски проходят большой путь, прежде чем удариться о поверхность земли. Поэтому при анализе ситуации аварийного подрыва одним из определяющих параметров является момент его осуществления.

Степень риска для обслуживающего персонала характеризуется вероятностью поражения человека, которая, в свою очередь, определяется математическим ожиданием несчастного случая и позволяет предсказать возможное число этих случаев, если произошло падение обломков и топлива на землю и эти обломки взорвались (дефлагировали).

Для правильной оценки математического ожидания числа несчастных случаев необходимо учитывать следующие факторы, которые могут быть сгруппированы в две категории:

— характеристики ЛА, которые определяют расчетную дальность, вероятность возникновения неисправностей в полете, количество и тип топлива, а также характер разлета частей ЛА под действием аэродинамических сил и в результате срабатывания системы аварийного подрыва;

— характеристики внешних условий, которые определяются расположением стартовой позиции и азимутом пусков, направлением и скоростью ветра, распределением обслуживающего персонала вблизи трассы полета.

Разработка математической модели, в которой уровень опасности для данной населенной территории выражается через вышеупомянутые факторы, позволяет не только найти математическое ожидание несчастного случая, но и предсказать вероятность смертельных исходов, если оперировать соответствующими параметрами.

Модель строится в предположении, что подверженная опасности падения обломков территория имеет зоны с различной степенью защищенности, а обслуживающий персона распределен по этим зонам:

S₁— территория под открытым небом;

S₂ — территория легких построек;

S₃ — территория фундаментальных зданий.

Пусть в пределах области S имеется n уровней защищенности, а площади, характеризуемые этими уровнями, обозначаются через S_i(i=1,2,...,n); N _i — число людей, находящихся в области S_i и имеющих уровень защищенности i -й зоны, а Р _ij — вероятность того, что j-й обломок ЛА упадет на площадь S_i. Этому обломку соответствует n зон несчастного случая 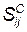— по одной для каждого уровня защищенности. Под зоной несчастного случая подразумевается площадь, окружающая точку падения обломка, граница которой является геометрическим местом точек, вероятность несчастных случаев в которых равна 0,5.

В частности, для взрыва зона несчастных случаев — это круг, а зона смертельного исхода — это окружность, на которой вероятность гибели людей составляет 0,5.

Следует отметить, что при увеличении степени защищенности, зона несчастного случая уменьшается.

Математическое ожидание несчастного случая на площади S_j от j-го обломка ЛА определяется по формуле

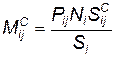, (4.102)

где Р _ij — вероятность того, что j-й обломок упадет на площадь S _i; N_i — количество людей, равномерно распределенных на площади S _i; 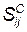— зона несчастного случая на площади S _i от j-го обломка; S_i — площадь с i-м уровнем защищенности.

Если просуммировать это выражение по всем обломкам j и по всем уровням защищенности i, то получим математическое ожидание несчастного случая на всей территории от действия всех обломков

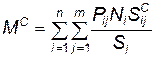. (4.103)

Если S мало, то вероятность падения j-го обломка в заданную точку будет одинакова по всей площади S и составит

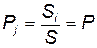, (4.104)

а уравнение (10.103) примет вид

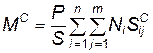. (4.105)

Если ввести обозначения 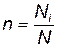— часть всего обслуживающего персонала, соответствующего i-му уровню защищенности; 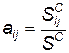— отношение площади зоны несчастного случая, соответствующей i-му уровню защищенности, к суммарной площади зон несчастных случаев, то можно выражение (4.103) записать так:

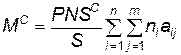, (4.106)

где 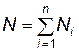количество обслуживающего персонала, находящегося на площади S; 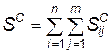— суммарная площадь зон несчастного случая.

Следует отметить, что размеры области, для которой справедливо равенство Р = Р _ij, зависят от расположения ее относительно точки запуска ЛА и расчетной траектории полета этого аппарата.

Определение площади зоны несчастного случая от осколков. Зоной несчастного случая является та область, на которой человек мог бы получить травму от прямого попадания падающего или рикошетирующего обломка ЛА или избыточного давления, явившегося следствием взрыва ступени ЛА. Эта зона является функцией времени, так как она уменьшается с увеличением времени полета из-за выгорания топлива.

Детально описать форму и массу каждого куска из всей совокупности осколков не представляется возможным. Поскольку некоторые приборы, узлы и элементы конструкции ЛА остаются неповрежденными, то для этих элементов площадь зоны несчастного случая может быть определена на основании чертежей. Однако куски горящего топлива имеют разнообразную форму и размеры, а поэтому точное определение зоны несчастных случаев для них невозможно и имеет смысл предположить, что все эти куски имеют форму прямоугольных параллелепипедов.

Влияние присутствия человека на величину площади зоны несчастного случая, соответствующей отдельному осколку, может быть учтено увеличением этой зоны на величину площади, занимаемой стоящим человеком и принимаемой равной 0,186 м². Если осколок очень мал и падает на площадь 0,186 м², то все равно произойдет несчастный случай, т. е. минимальная зона несчастного случая 0,186 м². Если осколок имеет площадь большую, чем площадь, занимаемая человеком, то за пределами этой зоны на расстоянии 0,61 м от ее границы по крайней мере часть тела человека будет поражена.

Следовательно, зона несчастного случая, причиной которого являются осколки, получается с помощью преобразования плановой проекции осколка в равновеликий круг с последующим добавлением 0,61 м к его радиусу для учета размеров человеческого тела:

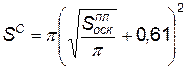, (4.107)

где S^C— площадь зоны несчастного случая от осколка; 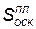— площадь проекции осколка в плане.

Это выражение позволяет вычислить площадь зоны несчастного случая, соответствующую каждому осколку, для людей под открытым небом.

Результаты, получаемые по этой формуле, имеют запас, так как формула дает завышенную оценку площади зоны несчастного

Определение площади зоны несчастного случая от ударной волны. Для определения избыточного давления в зависимости от расстояния и массы тротила существует несколько эмпирических формул. Одна из них, формула Кингери, выведена с помощью изменения давления при взрывах 5...I0O т тротила. Радиус, на котором ожидается данное значение максимального избыточного давления, определяется по формуле

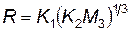, (4.108)

где R — расстояние до центра взрыва, м; К₂ — массовая часть, соответствующая тротиловому эквиваленту (по некоторым данным К₂=0,05÷0,2 для ЛА с РДТТ); М₃ — масса твердотопливного заряда в момент аварийного подрыва; K ₁ — коэффициент, зависящий от величины избыточного давления, при котором определяется R.

Избыточное давление 14,7 КПа повреждает барабанные перепонки у человека, 35 КПа — повреждает легкие, а 70 КПа — может оказаться смертельным.

Если под несчастным случаем понимать повреждение барабанных перепонок, то площадь зоны несчастного случая определится из общей формулы

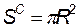(4.109)

подстановкой вместо R значения R ₀ ,₁₄:

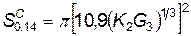. (4.110)

Избыточное давление 21 КПа приводит к несчастным случаям обслуживающего персонала, находящегося в легких деревянных постройках, а 35 КПа — в каменных постройках, причем деревянные постройки разрушаются полностью, а каменные здания могут быть как разрушены, так и частично повреждены.

Определение площади зоны несчастного случая от горящих осколков топлива. Оставшаяся невзорвавшаяся часть топлива (1- K ₂ ) G ₃ разбрасывается вокруг точки падения в виде горящих осколков.

Осколки имеют различную массу в зависимости от радиуса разлета, причем с увеличением радиуса масса осколков увеличивается. Средняя масса осколков на расстоянии R от центра взрыва определяется по формуле

G_R = K ₃ R ², (4.111)

где G_R — средняя масса осколка, кг; R — радиус от центра взрыва, м; К₃= 7,25·10^-6 — эмпирический коэффициент.

Количество осколков, приходящееся на единицу площади, с увеличением R будет уменьшаться и может быть определено из выражения

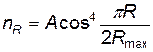, (4.112)

где R_max — максимальный радиус разброса, который для большинства аварий крупных ЛА составляет 760 м.

Вид представленных зависимостей (4.111) и (4.112) изображен на рис. 4.8.

Величина А определяется из условия сохранения массы топлива, которое может быть записано в функции от G_R и n_R:

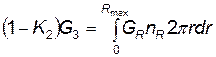, (4.113)

где 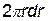— элементарная площадь кольцевой области шириной dr.

Подставляя в уравнение (4.113) значения G_R и n _R из (4.111) и (4.112) и решая его относительно А, получаем

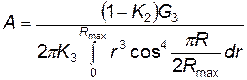. (4.114)

Анализ фотоснимков показывает, что большинство несгоревших кусков — это прямоугольные параллелепипеды с размерами 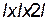. Поэтому, обозначив через 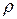удельный вес топлива, будем иметь

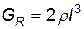. (4.115)

Подставляя в уравнение (4.115) значение G ₃ из (4.111) и имея в виду, что зона несчастного случая имеет размеры в плане 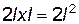, получаем среднюю площадь, занимаемую одним осколком:

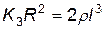
или

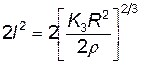. (4.116)

С учетом размеров человеческого тела площадь зоны несчастных случаев определится по формуле (4.107), если в нее вместо 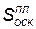подставить 2 l ² из (4.116):

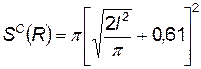. (4.117)

Общая площадь зон несчастных случаев, которые могут произойти с обслуживающим персоналом под открытым небом при падении ЛА, представляет собой сумму произведения средней площади зоны несчастного случая от одного осколка и числа осколков, приходящихся на единицу площади:

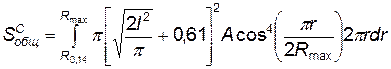. (4.118)

Интервал интегрирования берется от R _0,14 — радиуса зоны несчастных случаев вследствие ударной волны на открытом пространстве, а не от нуля, так как несчастные случаи внутри зоны радиуса R _0,14 уже учтены.

Следует отметить, что с помощью уравнения (4.118) можно получить площадь зон несчастных случаев для людей под открытым небом. Если необходимо определить эту площадь для людей, находящихся в строениях, то за нижний предел интегрирования необходимо взять радиус, на котором осколки имеют достаточные размеры, чтобы пробить легкие и фундаментальные строения соответственно.

Выше указывалось, что ударяющаяся о землю часть топлива G ₃ является линейной функцией как времени полета ЛА, так и времени ее падения после взрыва, а поскольку время падения может быть выражено в виде линейной функции промежутка времени между стартом и моментом аварийного подрыва, то для большинства случаев G ₃ можно выразить так:

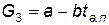, (4.119)

где a и b — константы, зависящие от физико-химических характеристик топлива; t _а.п — время от момента запуска двигателя до момента аварийного подрыва.

Для площади зон несчастных случаев, вызываемых ударной волной и горящими осколками топлива, можно записать выражение

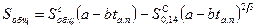, (4.120)

где 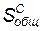— общая площадь зоны несчастных случаев от горящих осколков, определяемая по формуле (4.118); 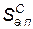— общая площадь зоны несчастных случаев от ударной волны на открытой территории, определяемая по формуле (4.118).

Подобные выражения могут быть написаны и для вычисления площадей зон несчастных случаев среди обслуживающего персонала, находящегося в легких и фундаментальных строениях, при воздействии ударной волны и горящих осколков.

Части конструкции и оборудования ЛА, которые при подрыве аппарата не разделяются на куски (батареи, сопла, электронные блоки), должны быть исследованы с целью определения скорости удара этих частей для оценки глубины их проникновения в преграду.

В приведенной выше математической модели определения вероятности несчастного случая (математического ожидания несчастного случая) было принято допущение, что аварийная система подрыва не инициирует (не вызывает) детонацию твердого топлива как в воздухе, так и при ударе кусков о поверхность грунта.