4.3.1. Определение степени готовности КСНО к применению
Наиболее важной характеристикой, объединяющей свойства ЛА, КСНО и условия их применения, является эффективность комплекса ЛА данного типа. Она характеризует степень пригодности комплекса по назначению.
Эффективность КСНО является составной частью эффективности комплекса ЛА и может быть представлена в виде произведения двух независимых случайных величин:
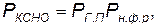 (4.45)
(4.45)
где РГ.П — вероятность готовности КСНО к применению; Рн.ф.р — вероятность нормального функционирования элементов КСНО при выполнении задачи.
Вероятность готовности КСНО к применению характеризует два независимых случайных события:
— вероятность того, что в произвольный момент времени комплекс будет находиться в исправном состоянии;
— вероятность того, что в нужный момент времени комплекс не будет поражен противником, т. е.
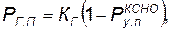 (4.46)
(4.46)
где КГ — коэффициент готовности КСНО, определяющий вероятность того, что в произвольный момент времени комплекс будет находиться в исправном состоянии;
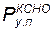 — условная вероятность поражения КСНО.
— условная вероятность поражения КСНО.
Определение коэффициента готовности КСНО. Процесс эксплуатации КСНО можно представить как чередование периодов исправного и неисправного состояний (рис. 4.5, где А — нерабочее состояние, комплекс исправен; В — рабочее состояние, комплекс исправен; С — нерабочее состояние, неисправность не выяснена; D — состояние восстановления).
Переходы из одного состоянии в другое характеризуются следующими интенсивностями:
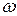 — средняя (отнесенная к сроку эксплуатации) интенсивность назначений на работу;
— средняя (отнесенная к сроку эксплуатации) интенсивность назначений на работу;
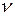 — средняя интенсивность выполнения работы (величина, обратная средней продолжительности одного периода работы)
— средняя интенсивность выполнения работы (величина, обратная средней продолжительности одного периода работы)
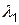 — средняя интенсивность возникновения отказов в нерабочем состоянии;
— средняя интенсивность возникновения отказов в нерабочем состоянии;
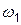 — средняя интенсивность работ по обнаружению неисправностей (внешние осмотры и другие виды контроля, не связанные с наработкой комплекса);
— средняя интенсивность работ по обнаружению неисправностей (внешние осмотры и другие виды контроля, не связанные с наработкой комплекса);
 — средняя интенсивность возникновения отказов в рабочем состоянии;
— средняя интенсивность возникновения отказов в рабочем состоянии;
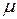 — средняя интенсивность восстановления.
— средняя интенсивность восстановления.
Функционирование комплекса происходит следующим образом. Из состояния А комплекс может перейти либо в состояние В, либо в С. Назначение комплекса на работу соответствует переходу в В и идет с интенсивностью 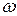 . После работы исправный комплекс переходит в состояние А. Если во время работы происходит отказ, то комплекс с интенсивностью
. После работы исправный комплекс переходит в состояние А. Если во время работы происходит отказ, то комплекс с интенсивностью  переходит в состояние D. Беля отказ возник в состоянии А, то комплекс переходит в состояние С с интенсивностью
переходит в состояние D. Беля отказ возник в состоянии А, то комплекс переходит в состояние С с интенсивностью 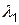 , а восстановление идет с интенсивностью
, а восстановление идет с интенсивностью 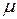 . После восстановления — переход в А, назначение же на работу из состояния С происходит с интенсивностью
. После восстановления — переход в А, назначение же на работу из состояния С происходит с интенсивностью 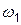 .
.
Необходимо отметить, что в состоянии С могут возникать неисправности с той же интенсивностью, что и в состоянии А. Однако возникновение этих новых неисправностей не означает перехода в другое состояние: комплекс продолжает оставаться в состоянии С до тех пор, пока не будет установлено, что он неисправен.
Возникновение в нерабочий период двух и более неисправностей отражается на затратах времени на восстановление. Как правило, межрегламентный период эксплуатации меньше среднего времени нахождения в исправном состоянии, когда комплекс не работает. Поэтому вероятность возникновения более одной неисправности в период между работами можно считать малой.
В произвольный момент времени комплекс может находиться только в одном состоянии. Определим вероятности пребывания комплекса в каждом состоянии.
Будем считать, что потоки переходов с интенсивностями 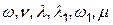 являются стационарными пуассоновскими, а процесс функционирования комплекса в этом случае можно считать марковским.
являются стационарными пуассоновскими, а процесс функционирования комплекса в этом случае можно считать марковским.
Стационарным потоком событий называется поток, для которого вероятность появления того или другого числа событий на участке времени 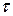 зависит лишь от длины этого участка и не зависит от того, где по оси времени взят этот участок.
зависит лишь от длины этого участка и не зависит от того, где по оси времени взят этот участок.
Пуассоновский поток — это поток, обладающий свойствами ординарности и отсутствия последействия.
Поток событий называется ординарным, если вероятность того, что на малый участок Δt, примыкающий к моменту времени t, падает больше одного события, пренебрежимо мала по сравнению с вероятностью того, что на этот же интервал времени попадает ровно одно событие.
Отсутствие последействия заключается в том, что для любых пересекающихся участков 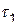 и
и 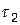 число событий, попадающих на один из них, не зависит от того, сколько событий попало на другой.
число событий, попадающих на один из них, не зависит от того, сколько событий попало на другой.
Процесс называется марковским, если состояние системы Xi в некоторый момент времени определяет лишь вероятность Pij ( t ) того, что через промежуток времени t система будет находиться в состоянии Xj, причем эта вероятность не зависит от течения процесса в предшествующий период.








