Если условие, проверяемое оператором, P 8 ( t H j < Т) выполнено, то управление передается оператору Ф9. В результате работы операторов Ф9 и Ф10 формируются tj оп и tj K.

Дата: 2025-06-14; Просмотры: 6

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Далее переходим к проверке условия 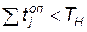(операторы А₁₁ и Р₁₂), т. е. к проверке необходимости наладки обрабатывающего агрегата из-за износа. Если условие, проверяемое Р₁₂, выполнено (в наладке необходимости нет), то переходим к формированию времени подготовки агрегата к следующей операции (оператор Ф₁₄) после i-1 операции, определению момента готовности агрегата к обработке нового элемента ЛА (оператор А₁₅) и формированию значений параметров элемента ЛА после обработки (оператор Ф₁₆). В случае наладки агрегата (условие, проверяемое оператором Р₁₂, не выполнено, оператор Ф₁₃ формирует время наладки t ^нал и конца наладки Т^нал и передает управления оператору А₁₅ для определения готовности агрегата к обработке нового элемента ЛА.

Вторая часть алгоритма непосредственно операцию обработки не моделирует, а обеспечивает связь и синхронизацию ее с другими актами технологического процесса подготовки ЛА (подача необработанных элементов ЛА), а также управление самим процессом моделирования (фиксация и обработка результатов, переход к очередному обрабатываемому элементу и т. д.). Эта часть алгоритма моделирует некоторую систему массового обслуживания. Оператор Ф₁ формирует случайные числа t_j ^П, которые имитируют поток однородных событий в соответствии с заданным законом распределения. Оператор Р₂ проверяет условие t_j ^П < Т_Г. Если это условие выполнено, то заявка поступает в систему и обслуживается.

Операторная схема алгоритма, моделирующего работу обрабатывающего агрегата, запишется в виде

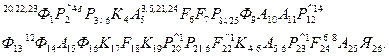
В операторной схеме приняты следующие обозначения:

A_N^К — арифметический оператор, означающий, что от оператора A_N управления передается к оператору К;

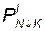— логический оператор, означающий, что от оператора P_N управление следует передавать оператору l, если условие, проверяемое

Р _N , выполнено, или же оператору К, если оно не выполнено;

^{n , l} Ф _N означает, что оператору формирования случайных процессов Ф _N управление передается от операторов n и I;

F_N — операторы формирования неслучайных величин;

К _N - счетчики.

В блок-схеме логический оператор обозначен ромбом, внутри которого записано проверяемое условие. Управление от логического оператора передается по стрелке, отмеченной единицей, если условие, проверяемое оператором, выполнено, и по стрелке, отмеченной нулем, если оно оказывается невыполненным.

Если появится необходимость в описании модифицированного процесса обработки, представленный алгоритм может быть легко видоизменен или дополнен другими операторами [25, 26].

4.1.4. Математическая модель операции сборки

Операция сборки представляет собой элементарный акт технологического процесса над совокупностью элементов ЛА (ведущим и ведомыми элементами), в результате которого изменяется значение хотя бы одного из параметров ведущего элемента ЛА (за счет присоединения к нему ведомых), а соответствующие ведомые элементы прекращают существование. Соответствующий набор технологического оборудования, обеспечивающий выполнение операции сборки, называется сборочным агрегатом.

Сущность формализованной операции сборки состоит в переработке информации, описывающей состояния элементов ЛА, которые участвуют в сборке.

Для многих технологических процессов подготовки ЛА выбор одного из элементов ведущим (сборный узел) оказывается условным, особенно для первых сборочных операций, свойственных начальному периоду сборки аппарата.

Если в сборке участвуют сборный узел (ведущий элемент) и m деталей (ведомых элементов), параметры которых к моменту начала сборки t ^H известны 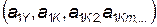, то в результате операции сборки мы получим новый узел с новыми значениями параметров а_{2 KY}, а детали прекратят существование. Математически операция сборки описывается соотношениями вида

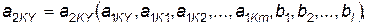(4.6)

где b_i — параметры, зависящие от характеристик сборочного агрегата. Определение моментов прекращения существования ведомых элементов проводится лишь в случае необходимости или принимается равным t^H или t ^к.

Если а_{2 KY} могут принимать случайные значения, то по аналогии с (10.3) имеем

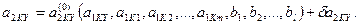(4.7)

При нахождении параметров, определяющих синхронизацию элементов операции сборки, могут быть использованы следующие соображения. Если 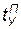— момент поступления на сборку узла, а 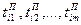— моменты поступления деталей и операция начинается в момент готовности всей совокупности элементов, то по аналогии с (4.4) можно записать

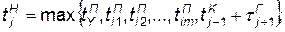. (4.8)

Если отдельные сборочные работы (части операции сборки) начинаются по мере поступления на сборку тех или иных элементов ЛА или по мере готовности определенных агрегатов сборки, то целесообразно рассматриваемую операцию сборки расчленить на несколько последовательно выполняемых операций.

Другим существенным параметром, определяющим режимы взаимодействия отдельных элементов оборудования во времени, является продолжительность операции сборки. При формализации операцию сборки удобно представить в виде последовательности этапов, которые условно можно назвать установкой элемента на узле; креплением элементов; регулировкой узла. В соответствии с этим и длительность операции рассматривается как сумма трех слагаемых, которые в общем случае являются случайными с заданными вероятностными характеристиками.

Следует отметить, что обычно при описании операции сборки определяются параметры только сборного узла, а параметры ведомых элементов не фиксируются. Это в значительной мере упрощает соотношения вида (4.6) и (4.7).

Составим модель функционирования операции сборки. Пусть операцией сборки предусматривается присоединение к подготавливаемому ЛА (ведущему элементу) нескольких ведомых элементов. Если в необходимый момент времени соответствующий ведомый элемент подан на сборку, то операция сборки происходит, в противном случае сборка срывается. Если ведомый элемент оказывается негодным, он заменяется другим. Операция сборки продолжается (t ^СБ) ограниченное время 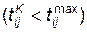. После окончания сборки и получения готового изделия или срыва операции сборки переходим к сборке последующего ЛA (t ^п < Т). Вероятность Р^НГ того, что ведомый элемент может оказаться негодным известна, известно также время t ^пр, затрачиваемое на проверку этого элемента.

Для построения моделирующего алгоритма операции сборки введем следующие операторы:

Ф₁ — формирование момента поступления ведущего элемента на сборку;

Р₂ — проверка условия t_j ^П < Т;

Р₃ — проверка условия I > l _пр, где i — номер ведомого элемента, а l _пр — количество присоединяемых элементов;

Ф₄ — формирование параметров ЛА после сборки ;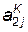

К₅ — счетчик количества готовых ЛА, реализующий операцию N+1;

К₆ — счетчик номеров ведущих элементов, реализующий операцию j+1;

F ₇ — формирование i = 1;

F ₈ — переход к новому ведущему элементу;

F ₉ — подготовка к i -й сборочной операции;

Р₁₀ — проверка условий n_i > 0, где n_i — количество ведомых элементов номер i, имеющихся в ведущем элементе;

К₁₁ — счетчик количества срывов операции сборки;

К₁₂ — счетчик количества элементов номер i, реализующий операцию n_i- 1;

Ф₁₃ — формирование значения t^np;

Р₁₄ — проверка условия ξ < Р^НГ, где ξ — случайное число с равномерным распределением в интервале [0, 1];

Ф₁₅ — формирование длительности операции t ^СБ;

А₁₆ — определение момента 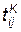окончания i-й операции с учетом потери времени t ^пр;

Р₁₇ — проверка условия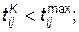

К₁₈ — счетчик номеров сборочных операций, реализующий операцию I +1;

F ₁₉ — формирование I = i +1, т. е. имитация конца сборки;

К₂₀ — счетчик количества готовых ЛА, реализующий операцию N-1;

A ₂₁ — обработка результатов моделирования;

Я₂₂ — выдача результатов.

Блок-схема моделирующего алгоритма операции сборки представлена на рис. 4.3.

Операторная схема моделирующего алгоритма для составной операции сборки

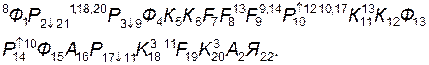
Сущность работы алгоритма.

Оператор Ф₁ формирует момент поступления на сборку j-го ведущего элемента t _j ^П. Величина t _j ^П сравнивается с Т (оператор Р₂), где Т— предельное время операции сборки < какое-то контрольное время). Если t _j ^П < T, то моделирование продолжается, в противном случае управление передается оператору А₂₁ для обработки результатов моделирования.

Оператор Р₃ проверяет условие I > l, если I > l, то это значит что сборка данного элемента ЛА закончена и осуществляется переход к новому сборному узлу j+1 (оператор F ₈) с попутным формированием 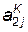(оператор Ф₄), подсчетом количества готовых ЛА (оператор К₅), определением номера нового сборного узла (оператор К₆) и формированием i = 1 (оператор F ₇).

Если же условие, проверяемое оператором Р₃ не выполнено, то сборка элемента ЛА не закончена и осуществляется переход к оператору F ₉ для подготовки к очередной сборочной операции.

Оператор Р₁₀ поверяет, имеются ли n_i > 0 детали, необходимые для сборки. Если деталей нет, то происходит срыв сборки (как i-й сборочной операции, так и составной операции) и управление передается оператору К₁₁ для подсчета количества срывов, а затем оператору F ₁₉, который формирует I = l+1, т. е. имитирует конец сборки, а оператор К₂₀ вычитает единицу из количества готовых элементов ЛА для компенсации действия оператора К₅. Управление передается оператору Р₃. Теперь I > l, поэтому работа алгоритма будет продолжаться по знакомой нам цепи Р₃Ф₄...F ₈ Ф₁.

Если условие n_i > 0 выполняется (оператор Р₁₀), т. е. детали для сборки есть, то управление передается оператору K ₁₂, который вычитает единицу из n_i (деталь взята для проверки), Ф₁₃ формирует длительность проверки t^np. Затем по жребию (оператор P ₁₄) определяется качество детали. Если деталь негодна, то возвращаемся к P ₁₀ и выбираем новую деталь, а если деталь годна, то продолжаем сборку: оператор Ф₁₅ формирует длительность, а A ₁₆ определяет момент окончания i–й операции сборки 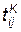. Если 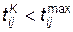(оператор Р₁₇), то переходим к К₁₈ (i+1), а затем к Р₃. Если это условие не выполнено, то получается срыв сборки (оператор К₁₁).

На практике встречаются и другие, более сложные модификации операции сборки. Их моделирование требует соответствующего изменения моделирующего алгоритма. Так, в рассмотренном примере предусматривалось, что отсутствие детали (n_i = 0) приводит к срыву сборки. Часто более приемлемым оказывается предположение, что при отсутствии детали сборный узел ожидает ее появления какое-то время и уже в противном случае происходит срыв сборки.

4.1.5. Математическая модель операции управления

Операция управления вырабатывает информацию, необходимую для согласованной работы отдельных элементов КСНО в технологическом процессе предстартовой подготовки ЛА. Операции управления сами по себе не изменяют параметров аппарата, не оказывают влияния на его физические свойства и непосредственного отношения к обработке и сборке не имеют. Однако в результате операции управления мы получаем информацию о требуемых изменениях в режимах работы отдельных агрегатов и в строении технологического процесса подготовки ЛА заданным комплексом наземного обслуживания.

Существует некоторый набор оборудования, называемый управляющим устройством, который обеспечивает операцию управления. Реально операцию управления может выполнить и человек-оператор, но принципиального значения с точки зрения математического описания это не имеет, поскольку в данном случае рассматриваются лишь те действия, которые легко формализуются.

В общем виде информацию о требуемых изменениях в режимах работы отдельных агрегатов технологического оборудования можно записать в виде

,

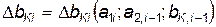где b_Ki — параметры технологического оборудования на i-й операции, K= 1,2, ..., m; а_{1 i}, a _{2 i} — параметры обслуживаемого ЛА или его элемента до начала i-й операции и после ее окончания соответственно; Δ b _Ki — поправка, вносимая в параметры технологического оборудования.

Важным обстоятельством является привязка операции управления к времени выполнения определенной технологической операции. Если основной задачей управления является настройка оборудования на режим, соответствующий параметрам поступающего на обслуживание ЛА, то операция управления начинается после поступления аппарата к данному рабочему месту, а заканчивается до начала технологической операции. Если основной задачей управления является настройка оборудования на режим, соответствующий параметрам поступающего на обслуживание ЛА, то операция управления начинается после поступления аппарата к данному рабочему месту, а заканчивается до начала технологической операции. Если задача управления сводится к поддержанию стабильных значений параметров аппарата (а_{2 i} = const) или стабильных режимов работы оборудования (b_Ki = const), операция управления начинается после окончания очередной технологической операции. Иногда технологические операции и операции управления выполняются одновременно, что не влияет на сложность описания этого процесса.

Для описания ошибок, связанных со случайными флуктуациями параметров а_{1 i} , а_{2 i} и b_Ki, используются обычные способы задания вероятностных характеристик.

Одним из простейших приемов моделирования операция управления является воспроизведение в модели технологического процесса алгоритма управления в виде подпрограммы. Если появляется необходимость в воспроизведении процесса функционирования управляющего устройства (например, для учета надежности), эти устройства могут быть представлены в виде сравнительно простых формализованных схем, для которых моделирующие алгоритмы близки к алгоритмам операций обработки в сборки.

4.2. Аналитические модели процесса подготовки ЛА

4.2.1. Общая постановка задачи обслуживания

Одним из главных вопросов, решаемых при создании КСНО, является разработка принципов исследования и методики анализа качества функционирования комплекса, позволяющих определить основные проектные параметры и характеристики отдельных агрегатов обслуживания с учетом взаимосвязи между ними. Такая задача требует от проектанта разработки математических моделей, позволяющих на этапе предварительных изысканий априорно отрабатывать различные варианты проектных решений и проверять реализуемость выполнения предъявляемых к системам наземного обслуживания требований.

Для оценки качества функционирования КСНО в процессе проектирования необходимо определить:

- количество рабочих мест на ТП и СП;

- целесообразность проведения на стартовой позиции текущего ремонта ЛА;

- средний темп пополнения ЛА, необходимых для замены списанных в процессе эксплуатации; ,

- необходимое количество транспортных агрегатов, средств заправки и т. п.

В качестве исходных данных при проектировании систем наземного обслуживания можно выбрать:

- количество ЛА и их типы, обслуживаемые данным комплексом;

- расстояние между ТП и СП;

- интенсивность отказов ЛА при различных режимах наземного обслуживания;

- интенсивность восстановления работоспособности ЛА после отказов;

- среднее время сборки ЛА, его заправки и снаряжения.

Для выбора оптимального состава и структуры необходимо определить цели и задачи КСНО, рассмотреть особенности его структуры и процесса функционирования, а также выбрать критерии качества функционирования как всего комплекса в целом, так и его отдельных элементов.

Будем рассматривать типовой КСНО, который состоит из следующих элементов:

- нескольких СП;

- транспортного оборудования;

- заправочного оборудования;

- рабочего канала СП;

- ремонтной бригады СП.

Целью функционирования комплекса является обеспечение заданной вероятности работоспособного состояния ЛА на всех пусковых устройствах стартовых позиций в рабочем режиме. Процесс функционирования КСНО заключается в переходе ЛА от одного агрегата обслуживания к другому и изменении состояния этих элементов.

Задачи составляющих КСНО определяются целью всего комплекса в целом:

— стартовая позиция должна обеспечить в любой момент времени пуск заданного числа ЛА, а система технического обслуживания СП должны обеспечить такой режим обслуживания ЛА, при котором время скрытого отказа и время восстановления рабочего канала минимальны;

— техническая позиция, ремонтная бригада, транспортное оборудование и система заправки должны обеспечить бесперебойное обслуживание потока поступающих ЛА.

Математически задача выбора оптимального состава и структуры систем наземного обслуживания с заданными функциональными возможностями при ограничениях на показатели качества функционирования может быть сформулирована следующим образом.

Определить такие векторы 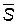состава КСНО и качества его элементов 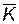, при которых стоимость комплекса минимизируется, т. е. C = C ( 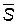, K ) 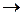min, при условии выполнения ограничения на уровень показателя качества функционирования, например вероятность выполнения поставленной задачи не ниже заданной, т. е. 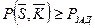. В данном случае 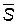= (S₁, S₂,…,S_n) — вектор состава КСНО; 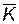= (К₁, К₂,...,К_n) — вектор качества элементов комплекса; n — количество функционально необходимых элементов комплекса.

Решение поставленной задачи осуществляется следующим образом. При фиксированном значении величин, характеризующих состав комплекса, определяется вектор параметров качества систем наземного обслуживания, обращающей функцию стоимости в минимум. После этого для полученного таким образом вектора качества выбирается оптимальный вектор параметров, характеризующих состав комплекса. Процесс поиска прекращается при таком сочетани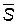и и 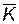, которое обращает функцию стоимости в минимум.

4.2.2. Математическая модель процесса функционирования КСНО

Для решения поставленной в предыдущем параграфе задачи выбора оптимального состава и структуры КСНО необходимо составить абстрактную модель процесса его функционирования.

Движение ЛА по технологической цепи подготовки к пуску от момента доставки аппарата с завода-изготовителя на ТП до момента старта требует участия всех элементов комплекса наземного обслуживания. При этом обслуживание ЛА тем либо другим агрегатом тесно связано с определенным состоянием обслуживаемого аппарата, т. е. процесс, при котором отдельные элементы комплекса обмениваются ЛА, определяется изменением состояний ЛА. Следовательно, можно установить строгое соответствие между состоянием ЛА и тем элементом комплекса, на котором он находится или которым обслуживается.

В процессе функционирования КСНО изменяется не только состояние ЛА, но и состояние исполнительных элементов комплекса. Так, вероятные состояния стартовой позиции могут быть описаны в виде графа (рис. 4.4).

На рис. 4.4 Х_о — состояние стартовой позиции, когда все n ЛА находятся в рабочем положении; Х₁ — состояние СП, когда (n-1) ЛА находятся в рабочем положении, а один ЛА — в нерабочем состоянии; X_i — состояние СП, когда (n - i) ЛА находится в рабочем положении, a i аппаратов находится в нерабочем состоянии; Х _n — состояние СП, когда ни один ЛА не находится в рабочем положении, СП полностью неработоспособна.

Очевидно, что указанные (n+1) состояния составляют полную группу событий, т. е. 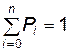, где P_i — вероятность нахождения СП в состоянии Х _i .

Следует отметить, что в состоянии Х _i , когда (n-1) ЛА находятся в рабочем положении, не все (n - i) аппаратов могут оказаться работоспособными, поскольку некоторые из них могут оказаться в состоянии скрытого отказа. Поэтому для каждого состояния X_i можно выделить подмножество состояний X_ij, где j = 0, 1, 2,..., n - i; Х_ij — состояние СП, когда (n - i) ЛА находятся в рабочем положении, причем (n - i - j) из них в работоспособном состоянии, а j — в состоянии скрытого отказала, {Х _{i 0} , Х _{i 1} ,..., X_ij ,..., X_{i ( n - i +1)} ; X_{i ( n - i )}} — возможное число состояний, равное (n - i+1). Выражение для полной группы событий в этом случае запишется следующим образом:

,

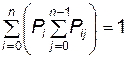где P_ij - вероятность того, что СП находится в состоянии X_ij .

Для ТП, транспортного оборудования и ремонтной бригады схему функционирования можно представить как обслуживание потока заявок при условии существования некоторого числа каналов обслуживания по каждой службе:

Х₀ — данный элемент системы наземного обслуживания (ТП, ТО, РБ) не загружен, ЛА отсутствуют, все каналы свободны;

Х₁ — элемент комплекса наземного обслуживания, на котором находится один ЛА, обслуживает этот ЛА один канал, остальные каналы свободны,

X_i — элемент системы обслуживания имеет i заявок на обслуживание, из них n обслуживается, а остальные ждут очереди (n — количество каналов обслуживания).

Моделирование процесса функционирования заправочного оборудования зависит от выбранного способа заправки обслуживаемых ЛА [56].

Если заправка ЛА осуществляется через централизованную заправочную систему (ЦЗС), процесс функционирования такой системы представляет собой последовательное изменение числа заправляемых ЛА, подготавливаемых к заправке, находящихся одновременно под заправкой ЛА и аппаратов, на которых производятся послезаправочные операции. При этом процесс поступления ЛА на заправку зависит как от технологического процесса предстартовой подготовки ЛА, так и условий его эксплуатации, а, следовательно, определяется целым рядом случайных событий и поэтому носит стохастический характер. Обслуживание ЛА через ЦЗС зависит от того, в каком состоянии она находится к моменту поступления изделия на заправку. Состояние заправочной системы к моменту поступления ЛА на заправку определяется возможными состояниями составляющих элементов этой системы, а поэтому процесс обслуживания ЛА через ЦЗС является вероятностным. Анализ особенностей работы ЦЗС показывает, что наиболее адекватной моделью ее работы является многоканальная система массового обслуживания с числом каналов, равным количеству заправочных агрегатов, на вход которой извне поступает некоторый поток заявок. Поступающий поток заявок не входит в рассматриваемую систему массового обслуживания, а, следовательно, состояния источников этих заявок анализу не подвергаются, т. е. в данном случае мы имеем дело с разомкнутой системой массового обслуживания.

Таким образом, задаваясь исходными данными в виде количества ЛА и их типов, обслуживаемых данными заправочными системами; расстояния между хранилищем-накопителем и объектами; интенсивностей подачи заявок на обслуживание и их удовлетворение, находят варианты заправки взаимно удалённых объектов, удовлетворяющие заданному уровню технической эффективности, которые определяются средним допустимым временем на заправку. Однако при решении поставленной задачи не учитывались затраты, связанные с организацией заправки тем или иным способом. Ниже приводятся постановка задачи и схема решения выбора оптимального варианта обслуживания взаимно удаленных объектов, где в качестве показателя совершенства выбрана экономическая эффективность, т. е. стоимость реализации операции заправки, а допустимое время на выполнение заправочных работ является дисциплинирующим условием.

Если обслуживание взаимно удаленных объектов осуществляется подвижными агрегатами, то математическая модель процесса функционирования заправочной системы зависит от соотношения количества подвижных заправочных агрегатов и количества обслуживаемых ЛА. Если количество подвижных агрегатов равно количеству обслуживаемых объектов или больше него, стратегия обслуживания строится по следующей схеме:

а) определяется наилучший вариант среди стационарных агрегатов;

б) производится сравнение наилучшего варианта стационарного с подвижным.

Оценка же обслуживания ЛА меньшим количеством подвижного оборудования приводит к необходимости количественного анализа процесса удовлетворения заявок методом теории массового обслуживания. Заявки в этом случае поступают в различные, вообще говоря, случайные моменты времени, и работа каждого канала носит случайный характер, зависящий от вида и внутренней структуры потока заявок, числа каналов обслуживания и закона распределения времени обслуживания заявки каждым каналом. Обслуживание взаимно удаленных объектов подвижными агрегатами может моделироваться замкнутой системой массового обслуживания, в которой интенсивность потока заявок зависит от состояния этой системы, а сами источники заявок являются элементами той же системы.

Следует отметить, что при выборе целевой функции процесса функционирования системы наземного обслуживания необходимо, чтобы она была достаточно простой, имела прямую связь с целевым назначением комплекса и была чувствительной к изменению проектных параметров этой системы обслуживания.

Как указывалось выше, целью функционирования КСНО является обеспечение заданной вероятности работоспособного состояния ЛА на всех пусковых установках СП в рабочем режиме. Поэтому в качестве целевой функции КСНО логично выбрать коэффициент готовности рабочего канала СП, определенного по всем СП.

Оптимизация параметров СП, основной задачей которой является минимизация как времени нахождения рабочего канала в состоянии открытого отказа, так и времени восстановления рабочего состояния канала, может вестись по параметру 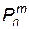, который соответствует вероятности нахождения не менее m рабочих каналов из n в работоспособном состоянии.

Техническая позиция, транспортное оборудование, ремонтная бригада и система заправки представляют собой систему массового обслуживания с неограниченным ожиданием, качество функционирования которых характеризуется показателями:

- вероятностью наличия очереди;

- средним временем пребывания заявки в системе;

- средним временем пребывания в очереди;

- средним временем простоя одного канала;

- вероятностью отказа в немедленном обслуживании;

- средним числом заявок в очереди и др.

Ниже рассмотрим более подробно моделирование процесса функционирования заправочной системы при различных способах подачи компонента к ЛА, расположенным на взаимном удалении друг от друга.

4.2.3. Моделирование процесса функционирования ЦЗС

Выше указывалось, что процесс заправки ЛА через ЦЗС представляет собой последовательное изменение числа подготавливаемых к заправке, находящихся одновременно под заправкой ЛА и аппаратов, на которых проводятся послезаправочные операции. Указывалось также, что система обслуживания ЛА через ЦЗС может быть отнесена к системе массового обслуживания разомкнутого типа с неограниченным ожиданием.

Определение параметров, характеризующих процесс обслуживания ЛА в этом случае, осуществляется путем исследования n-канальной системы массового обслуживания, на вход которой поступает простейший поток заявок с интенсивностью λ_и и интенсивностью обслуживания каждого канала μ_и. Если поступившая заявка застает свободным хотя бы один канал, она немедленно принимается на обслуживание и обслуживается до конца, в противном случае заявка попадает в очередь с максимальным количеством мест в очереди m. Очевидно, при m = 0 получается система массового обслуживания с отказами, а при m 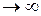— система с ожиданием. Каждая заявка может обслуживаться либо одним каналом (нет взаимопомощи между каналами), либо несколькими свободными каналами (есть взаимопомощь между каналами).

Если отсутствует взаимопомощь между каналами обслуживания, состояние системы массового обслуживания разомкнутого типа описывается с помощью следующей системы дифференциальных уравнений:

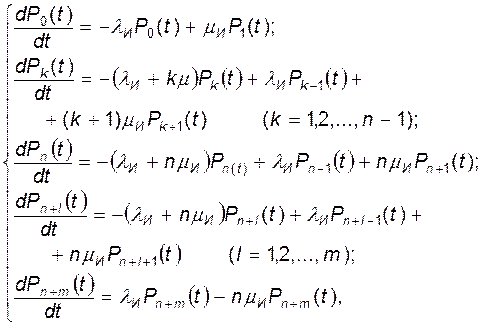(4.9)

где P_k ( t ) - вероятность того, что в момент времени t система будет находиться в состоянии Х_к;

Х_к — в системе имеется k заявок и они обслуживаются k каналами, очереди нет;

Х _{n + l} — в системе имеется n + l заявок, причем n из них обслуживается и l заявок находятся в очереди.

Интегрирование этой системы дифференциальных уравнений совместно с нормировочным условием

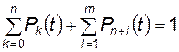(4.10)

позволяет найти все вероятные состояния системы массового обслуживания в произвольный момент времени в процессе выхода системы на стационарный режим, т. е. в процессе постановки ЛА на работу.

При стационарном режиме работы рассматриваемой системы массового обслуживания система уравнений (4.9) превращается в систему алгебраических уравнений вида

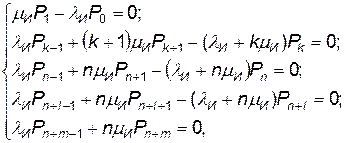(4.11)

которая решается совместно с нормировочным условием (4.10) и дает следующие зависимости для определения вероятностей нахождения системы в состояниях Х_к и Х _{n + l}:

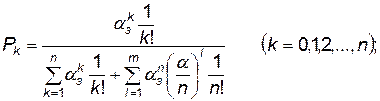(4.12)

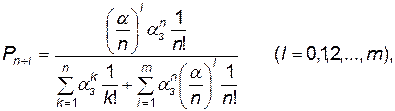(4.13)

где α₃ = λ/ μ— среднее число заявок, поступающих в рассматриваемую систему за среднее время обслуживания одной заявки одним каналом.

Зная вероятные состояния системы в любой момент времени, легко определить все параметры, характеризующие работу системы массового обслуживания.

Так, вероятность обслуживания заявки определяется вероятностью того, что к моменту поступления ее на обслуживание будут свободны хотя бы один канал или одно место в очереди:

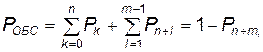, (4.14)

где Р _{n + m} определяется по формуле (4.15).

Далее может быть определено среднее число занятых каналов:

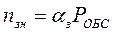^. (4.15)

Вероятность занятости любого канала в произвольный момент времени определится по формуле:

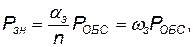(4.16)

где n — количество каналов обслуживания; ω₃ — среднее число заявок, поступающих в систему за среднее время обслуживания всеми каналами.

Вероятность того, что система полностью загружена, равна вероятности того, что в системе заняты все каналы:

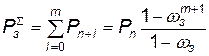. (4.17)

Среднее время неполной загрузки определяется из выражения

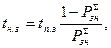(4.18)

где 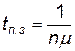- среднее время полной загрузки системы.

Среднее число заявок, находящихся в очереди:

. (4.19)

Среднее время ожидания заявок в очереди

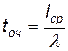. (4.20)

Среднее время нахождения заявки в системе складывается из среднего времени ожидания и обслуживания:

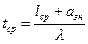. (4.21)

Таким образом определены основные параметры, характеризующие качество работы централизованной системы заправки при отсутствии взаимопомощи между каналами обслуживания.

Если существует взаимопомощь между каналами обслуживания, состояние системы массового обслуживания описывается с помощью системы дифференциальных уравнений вида

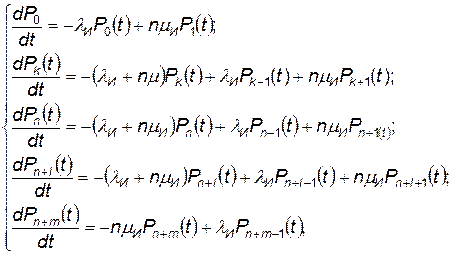(4.22)

которая в стационарном состоянии превращается в систему алгебраических уравнений

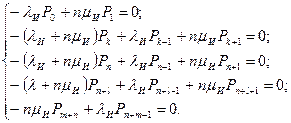(4.23)

Параметры, характеризующие работу такой системы массового обслуживания, определяются выражениями, аналогичными (4.14)-(4.21), в которых вероятности нахождения системы в состояниях Х _k и X_{n + l} находятся путем интегрирования системы уравнений (4.23) совместно с нормировочным условием (4.10) для случая постановки ЛА на дежурство и решением системы уравнений (4.23) и (4.10) для стационарного режима работы ЦЗС с взаимопомощью между агрегатами обслуживания. В частности, для стационарного режима работы вероятность пребывания системы в j-м состоянии (j = 0, 1, 2, ..., k, ..., n, ..., n + l, ..., n + m) находится из выражения

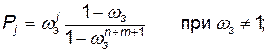(4.24)

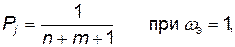(4.25)

где 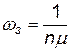— среднее число заявок, поступающих в систему за среднее время обслуживания всеми каналами.

4.2.4. Моделирование процесса функционирования системы заправки, осуществляемой подвижными агрегатами обслуживания

Работа системы заправки с помощью подвижных агрегатов обслуживания может быть смоделирована замкнутой системой массового обслуживания, в которой число источников заявок N ограничено количеством обслуживаемых ЛА, а интенсивность поступления заявок λ зависит от состояний источников, обусловленных работой самой системы. Такая задача обычно решается в следующей постановке.

Имеется N одинаковых взаимно удаленных объектов, каждый из которых может в некоторые случайные моменты времени подать заявку на обслуживание. Поток заявок каждого объекта считается пуассоновским с интенсивностью λ_и. Каждый объект обслуживается одним (нет взаимопомощи между каналами) или l из n (имеется частичная взаимопомощь) агрегатами обслуживания.

Интенсивность пуассоновского потока обслуживании каждого канала μ_и. Если к моменту подачи заявки объектом все каналы заняты, то этот объект становится в очередь на обслуживание; дисциплина очереди такая: кто раньше подал заявку, тот раньше обслуживается.

Для случая отсутствия взаимопомощи между каналами обслуживания состояние замкнутой системы массового обслуживания описывается системой дифференциальных уравнений вида

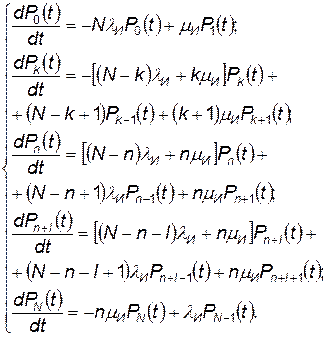(4.26)

Решение системы дифференциальных уравнений (4.26) совместно с нормировочным условием

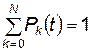(4.27)

позволяет определить все вероятные состояния замкнутой системы массового обслуживания и найти все параметры, характеризующие работу этой системы в режиме постановки ЛА на работу.

Для стационарного режима работы подвижных агрегатов обслуживания система (4.26) преобразуется в систему алгебраических уравнений вида

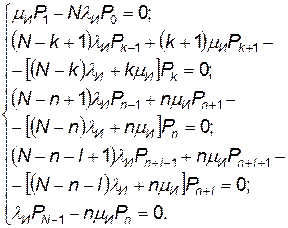(4.28)

Решение этой системы уравнений совместно с нормировочным условием (4.27) дает следующие выражения для определения вероятностей нахождения в состояниях Х_о, Х _k и Х _{n + l}:

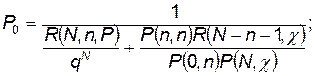(4.29)

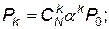(4.30)

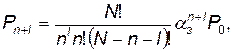(4.31)

где k=1, 2, 3, …, n; l=1, 2, 3, …, N - n , 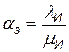; ; 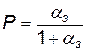q =1- P; 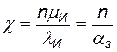; 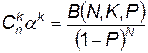вычисляются по таблице биномиального распределения;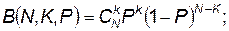

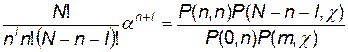вычисляются по таблицам пуассоновского распределения; ;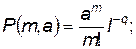

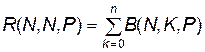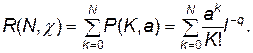
Таблицы пуассоновского и биномиального распределений всех указанных выше функций приведены в [54].

Зная вероятные состояния системы массового обслуживания замкнутого типа, легко определить и другие параметры, характеризующие процесс функционирования системы “заявка объекта — обслуживание агрегатом”. Так, среднее число обслуживаемых объектов 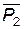определяется по формуле

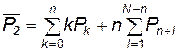. (4.32)

Среднее число ожидающих очереди объектов 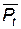можно найти так:

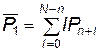. (4.33)

Среднее число простаивающих объектов

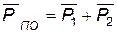. (4.34)

Коэффициент использования Р_ис (вероятность того, что определенный объект в любой момент времени будет работать и не нуждается в обслуживании) подсчитывают по формуле

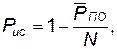(4.35)

где 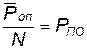— вероятность простаивания объекта, т. е. вероятность того, что объект нуждается в обслуживании.

Среднее время готовности объекта к применению будет

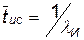. (10.36)

Среднее время простоя объекта и пребывания его в очереди определяется выражениями

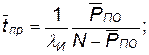(4.37)

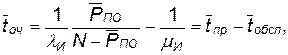(4.38)

где 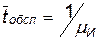— среднее время обслуживания одного объекта одним агрегатом.

Для случая работы замкнутой системы массового обслуживания с взаимопомощью между каналами обслуживания задача определения параметров функционирования формулируется следующим образом: имеется N одинаковых взаимно удаленных объектов, каждый из которых в любой случайный момент времени может подать заявку на обслуживание с интенсивностью λ_и; интенсивность обслуживания каждым агрегатом равна μ_и. Если подано заявок меньше 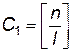, то каждый объект обслуживается одновременно l агрегатами, где 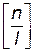— целая часть числа 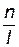. Производительность при этом возрастает в l раза и равна lμ_и. Величина l определяется максимальным числом агрегатов, которые могут быть использованы при обслуживания одного объекта. Если подано заявок С₂, причем С₁<С₂< n, то в обслуживании участвуют все n агрегатов, распределяясь приблизительно равномерно между всеми подавшими заявки объектами, при этом каждый объект обслуживается не более чем l агрегатами. Если подано заявок С₃, причем 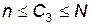, то в обслуживании участвуют все n агрегатов, которые обслуживают п объектов, а (С₃- n ) объектов ожидают очереди на обслуживание.

Процесс функционирования замкнутой системы массового обслуживания с взаимопомощью между каналами обслуживания описывается системой дифференциальных уравнений вида

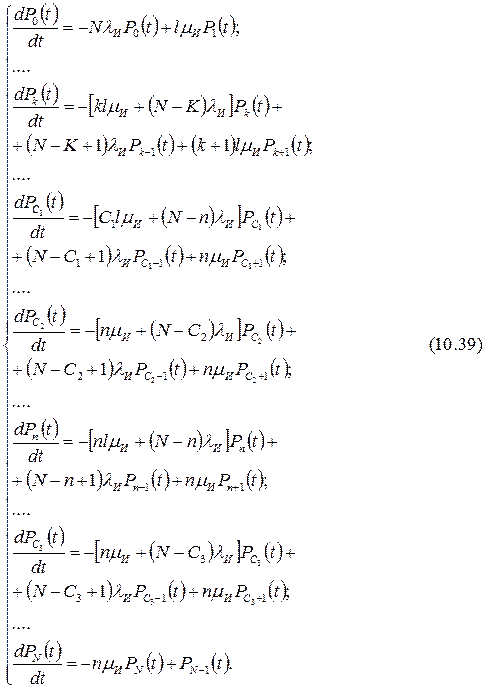
Эта система уравнений решается с нормировочным условием (4.27) и дает возможность определить параметры, характеризующие работу заправочной системы с помощью подвижных агрегатов обслуживания в режиме постановки ЛА на работу.

Для стационарного режима работы такой системы массового обслуживания система дифференциальных уравнений (10.39) преобразуется к виду

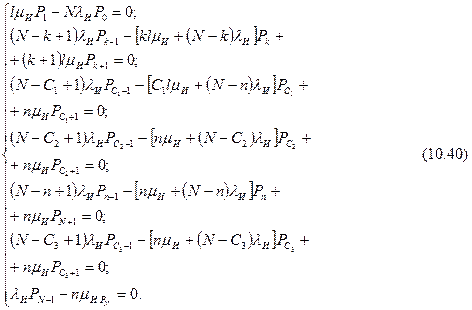
В результате решения системы алгебраических уравнений (4.40) совместно с условием (4.27) получаются следующие выражения для определения вероятных состояний подобной системы массового обслуживания:

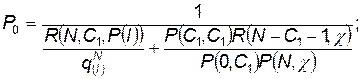(4.41)

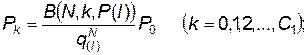(4.42)

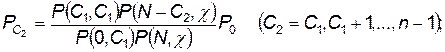(4.43)

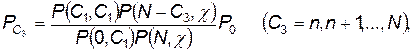(4.44)

где 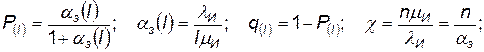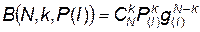— табличная функция биномиального распределения.

4.3. Анализ эффективности КСНО