4.1.3. Математическая модель операции обработки

Дата: 2025-06-14; Просмотры: 6

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Операция обработки представляет собой элементарный акт технологического процесса подготовки ЛА или его элемента, в результате которого меняется значение хотя бы одного из параметров этого аппарата. К абстрактной операции обработки относятся, в частности, технологические операции, связанные с изменением размеров элемента ЛА (членение), его положения в пространстве (транспортировка, повороты, подъемы) и сообщающие ему дополнительный признак (окраска, проверка) и т. д.

Комплекс технологического оборудования, обеспечивающий выполнение операции обработки, будем называть обрабатывающим агрегатом независимо от его реальной структуры и назначения. Построение математической модели операции обработки сводится к установлению соотношения между параметрами, характеризующими взаимодействие обрабатывающего агрегата и ЛА в процессе подготовки последнего к пуску.

Будем считать, что к моменту начала операции обработки t ^н известны значения всех параметров a _1К обслуживаемого ЛА или его элемента, тогда значение параметров а_2К для момента времени t ^К после операции будут определяться соотношениями вида

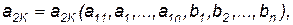(4.2)

где К= 1, 2, ..., n — количество параметров, характеризующих обслуживаемый ЛА или элемент; b_i — некоторые параметры, характеризующие обрабатывающий агрегат; t^K = t^H + 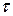, 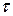— длительность операции обработки.

Поскольку параметры a _{1 K} и b _i могут оказаться случайными, то и a _{2 K} представляет собой случайную величину. В связи с этим независимо от природы возникновения флуктуации обычно в этом случае пользуются соотношениями вида

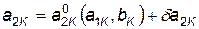, (4.3)

где δ a _2К — случайные отклонения величины а_2К от некоторого неслучайного значения а_{2 K} ⁰, заданные соответствующими законами распределения.

Кроме соотношений (4.2) и (4.3) операцию обработки описывают зависимости, определяющие режим функционирования обрабатывающего агрегата во времени. В том случае, когда отсутствует централизованное управление технологическими циклами во времени, операция может начинаться в любой момент времени при условии, что обрабатывающий агрегат готов к работе и к нему уже поступил очередной обслуживаемый ЛА или его элемент. Момент начала операции определяется как

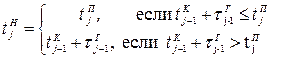, (4.4)

где t_j — момент поступления j-го ЛА к обрабатывающему агрегату;

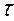^Г — время, затрачиваемое на подготовку агрегата к выполнению следующей операции.

В данном случае предполагается, что дополнительные простои оборудования исключаются либо включены в 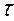^Г .

Время, затрачиваемое на подготовку агрегата к выполнению следующей операции, обычно является случайной величиной с показательным законом распределения

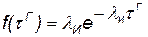, (4.5)

где λ_И— интенсивность отказов, зависящая от характеристик обрабатывающего агрегата и реже от характеристик обслуживаемого ЛА.

Время выполнения операции обработки зависит обычно как от свойств обрабатывающего агрегата, так и от параметров обслуживаемого ЛА или его элемента. Если обрабатывающий агрегат функционирует нормально и случайные колебания величины 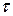несущественны, то длительность операции обработки является фиксированной неслучайной величиной. В более общем виде 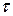представляет собой случайную величину, вероятностные характеристики которой определяют в предположении независимости ее от других случайных величин с точностью до двух моментов, т.е. находятся ее среднее значение и дисперсия.

Рассмотрим следующую формализованную схему операций обработки. Обслуживаемый ЛА с номером j поступает к i-му обрабатывающему агрегату в момент t_j ^Н и имеет параметры а ^j _{1 K}. Если обрабатывающий агрегат свободен, то он в момент t_j^H приступает к обработке ЛА. В противном случае ЛА неограниченное время ожидает освобождения агрегата. Когда количество m аппаратов в очереди достигает l _оч, подача их к обрабатывающему агрегату прекращается. Возобновление подачи ЛА производится по признаку m < l ₁. Операция обработки продолжается случайное время t^оп_i, зависящее от 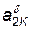и длительности работы обрабатывающего агрегата после наладки 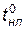. Наладка обрабатывающего агрегата начинается по времени 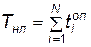и продолжается t _нл. Когда время t от начала процесса достигает значения Т, обработка нового ЛА не производится. Момент окончания операции обработки t^K определяется по известным t ^Н и времени занятости агрегата t _зн (с учетом t^{o п}, возможного ремонта, наладки и доработки). Таким же образом определяется и момент готовности агрегата к обработке нового ЛА: T ^Г = t^K + t ^Г , где t ^Г— случайная величина, имеющая смысл времени подготовки агрегата к операции.

Блок-схема алгоритма операции обработки представлена на рис. 4.2.

Для построения алгоритма, моделирующего описанную операцию обработки, введены следующие операторы:

Ф₁ — формирование очередного момента t_j ^П поступления ЛА к агрегату;

Р₂ — проверка условия t_j ^П < t ^Г;

Р₃ — проверка условия m > 1;

К₄ — счетчик количества m ЛА в очереди, реализующий операцию m +1;

А₅ — запись величин t_j ^П в специальные ячейки;

F₆ — переход к обработке очередного Л А;

F₇ — формирование t_j;

;

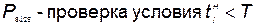Ф₉ — формирование значения t ^оп;

А₁₀ — определение t^K_j ( t^K_j = t ^Н _j + t ^зн );

А₁₁ — подсчет наработки агрегата ;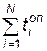

Р₁₂ — проверка условия ;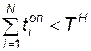

Ф₁₃ — формирование времени наладки t ^нл и конца наладки Т^нл;

Ф₁₄ — формирование случайных значений t ^Г;

А₁₅ — определение момента Т_Г;

Ф₁₆ — формирование значений параметров ЛА после обработки;

K ₁₇ — подсчет количества обработанных ЛА;

F ₁₈ — формирование момента готовности агрегата Т^Г;

К₁₉ — счетчик количества ЛА в очереди, реализующий операцию m-1;

P ₂₀ — проверка условия β > 0 (β = 0 означает, что подача ЛА прекращена; β = 1 — подача производится);

Р₂₁ — проверка условия m < l ₁;

F ₂₂ — формирование признака β = 1;

Р₂₃ — проверка условия m < l _оч;

F ₂₄ — формирование признака β = 0;

А₂₅ — обработка результатов моделирования;

Я₂₆ — окончание вычислений и выдача результатов.

Приведенный моделирующий алгоритм операции обработки состоит из двух частей. Первая часть, моделирующая непосредственно операцию обработки, начинается оператором Ф₉ и заканчивается Ф₁₆. Рассматривать ее, однако, удобнее с операторов F ₆ ,, F ₇ и P ₈.