3.17.2. Фазовая манипуляция (ФМ) дискретных сообщений
В зависимости от дискрета фазы Δφ наиболее часто используются разновидности ФМ, приведенные в табл.1,2.
Таблица 1
| Значение Δφ | Русское название | Международное название | Сокращенное название |
| π π/2 π/2 | Бинарная ФМ Квадратурная ФМ Квадратурная ФМ со смешением | Binary Phase Shift Keying Quadrature Phase Shift Keying Offset Quadrature Phase Shift Keying | BPSK QPSK OQPSK |
При бинарной ФМ возможно два значения начальной фазы сигнала: 0 или π, что позволяет различить единичный бит информации: 1 или 0.
При квадратурной модуляции возможно четыре значения начальной фаза сигнала: 0, π/2, π, 3π/4 или при смещении первого значения фазы на π/4 другая комбинация π/4, 3π/4, 5π/4, 7π/4. Поэтому здесь можно различать комбинацию из двух битов информации согласно табл.2.
Таблица 2
| Кодовая комбинация | ФМ без смещения | ФМ при смещение на π/4 | ЧМ |
| 11 01 10 00 | 0 π/2 π 3π/4 | π/4 3 π/4 5π/4 7π/4 | F1 F2 F3 F4 |
В результате, при квадратурной ФМ, объединяя нечетные биты с четными или одновременно передавая битовые комбинации от двух источников, можно, по сравнению с бинарной ФМ, в два раза увеличить объем передаваемой информаций за тот же по длительности сеанс связи. Смещение по начальной фазе осуществляется с целью лучшего различия одного символа от другого. Так, первый символ, определяемый с помощью N бит (в частности, N=8 или 16), передается без начального смещения фазы, второй символ - со смещением, 3-й символ - снова без смещения и т.д. Формирование ФМ сигнала как бинарного, так и квадратурного вида возможно с помощью процессора по специальной программе.
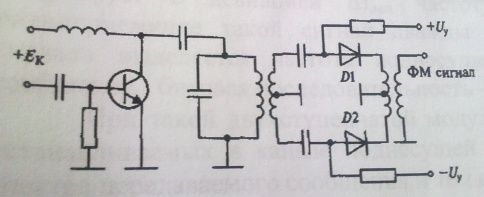 Реализация бинарной фазовой манипуляции сигнала с девиацией фазы Δφдев=π возможна с помощью схемы, приведенной на рис.3.31.
Реализация бинарной фазовой манипуляции сигнала с девиацией фазы Δφдев=π возможна с помощью схемы, приведенной на рис.3.31.
Рис.3.31. Схема бинарной фазовой манипуляции.
Фазовый модулятор содержит два электронных ключа, в качестве которых используются диоды. Открывая попеременно один или другой электронный ключ, снимают ВЧ сигнал с разных обмоток ВЧ трансформатора и тем самым скачком на Δφдев= π меняют фазу сигнала. (На схеме рис.3.31 отображен случай, когда диод DI открыт, а D2 закрыт.)
3.18. Частотная модуляция (ЧМ) дискетных сообщений
Применение одноступенчатой модуляции не позволяет во многих случаях реализовать преимущества ЧТ и ФТ. Это связано с тем, что в идеальном случае полоса пропускания радиоприемника должна быть равна спектру принятого сигнала. Практически данное требование из-за нестабильности частоты несущей передатчика и частоты гетеродина приемника реализовать не удается. Полосу пропускания приёмника, с учетом названных нестабильностей частот, приходится расширять, что снижает помехоустойчивость системы связи. Поэтому, более продуктивным оказывается двухступенчатая модуляция, при которой модулируется, сначала сравнительно низкая частота, поднесущая, а затем этой поднесущей модулируют несущую частоту радиопередатчика. Рассмотрим более подробно такой метод двухступенчатой модуляции на примере ЧТ - ЧМ, выполняемой согласно структурной схеме, приведенной на рис.3.32. В первой ступени модуляции сигнал, поступающий от источника информации, с помощью кодирующего устройства (кодера) преобразуется в последовательность двоичных символов - в биты информации. Далее в модуляторе 1 логической 1 присваивается частота F1 а логическому 0 - F2 (при фазовой модуляции им присваивались бы разные значения начальных фаз).
| Источник информации |
| Кодер |
| Модуля –тор 1 |
| Генератор 1 |
| Модуля -тор 2 |
| Генератор 2 |
| биты |
| ЧМ сигнал |
| F |
Рис. 3.32. Структурная схема двухступенчатой модуляции ЧТ-ЧМ
Далее синусоидальный сигнал с частотой F1 и F2 во второй ступени модулирует с девиацией Δfдев несущую частоту радиопередатчика. В радиоприемнике, принятый сигнал, дважды проходит процедуру демодуляции: сначала выделяется частота поднесущей, а затем - восстанавливается исходное цифровое сообщение - битовая последовательность.
При такой двухступенчатой модуляции полосы пропускания фильтров, устанавливаемых в канале поднесущей частоты, удается сузить до ширины спектра передаваемого сообщения и тем самым повысить помехоустойчивость.
Рассмотрим, как нужно выбирать частоты F1 и F2. Во-первых, следует обеспечить «плавный» переход, т.е. без скачка фазы, от сигнала с частотой F1 к сигналу с частотой F2 так, как показано на рис.,3.34 б. Это вызвано тем, что при скачке фазы происходит «размытие» мгновенного спектра сигнала, что снижает помехоустойчивость радиоприема и создает помехи другим системам радиосвязи. Во-вторых, значения этих частот, а точнее, соотношение между ними, должно быть таково, чтобы энергетический спектр модулированного сигнала был бы сконцентрирован в возможно узкой полосе, или не был бы «размыт». В-третьих, сигналы с частотами F1 и F2 должны быть ортогональны. Ортогональными называют сигналы, не перекрывающиеся во времени и с несовпадающими спектральными составляющими в частотном спектре.
Введем понятие среднего значения частоты поднесущей: Fср=0,5(F1+F2) и разности, или дискрета частоты, ΔF=F1 - F2. Тогда для частот, определяющих соответственно логические 1 и 0, запишем:
—для логической 1: F1=F0+0,5Δf=KFT;
—для логического 0: F2= F0-0,5Δf=NFT,
где FT=l/τ - частота следования элементарных посылок; К, N - числа, показывающие, сколько периодов частоты поднесущей укладывается внутри элементарной посылки, т. е. внутри одного бита, причем K>N.
Для дискрета частоты имеем AF=F i-F2=FT(K-N).
Фазы сигналов внутри элементарных посылок на протяжении одного бита изменяются по закону:
- внутри бита логической 1: φ1(t)=2πF1t=2πF0t+Δφ(t);
- внутри бита логического 0: φ2(t)=2πF2t=2πF0t+Δφ(t);
где  дополнительное изменение фазы сигнала:
дополнительное изменение фазы сигнала:
Δφ (t)= 2π0,5ΔFt = 2πF0(K-N)t.
К концу элементарной посылки, т.е. при t=τ = l/Fτ, дополнительный набег фазы на протяжении одного бита составит:
для логической 1: Δφ ==+π(K-N); для логического 0: Δφ = -π(К-N). 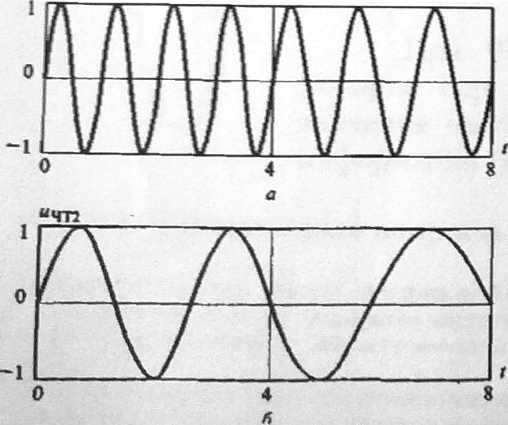
При K=l+N значение Δφ=+π для логической 1 и Δφ = -π для логического 0. Такой случай при К=4 и N=3 представлен на рис3.34, а, где логическая единица –F1 = 4Fτ; логический ноль - F2= 3Fτ.
Рис.3.34.. Формы битовых посылок при ЧМ для 1 и 0.
Можно, например, выбрать следующие значения параметров:
τ=1,28 мс или Fτ=781,25 Гц; F1=3125 Гц; F2=2343,75 Гц.
Разложим в ряд Фурье периодическое колебание прямоугольной формы (меандр):
y(Ωt)= 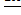 (
( 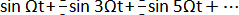 ) .
) .
Рассматривая колебание (рис,3.34,а), как сумму двух амплитудно-модулированных сигналов с частотами F1 и F2, с учетом последней зависимости для огибающей получим спектр, представленный при K=1+N на рис.3.35. (Сплошные линии относятся к сигналу с частотой F1 пунктирные к сигналу с частотой - F2 .) Из рассмотрения полученного спектра следует, что основная энергия сигнала сосредоточена в полосе ΔF=5Fτ, а выбранные сигналы ортогональны.
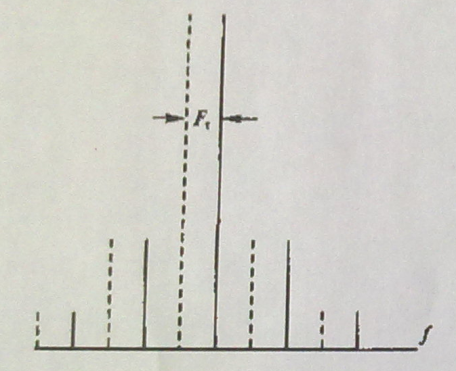
Рис.3.35.. Спектр сигнала при ЧМ битовых посылок.
Такой спектр можно еще более сузить при К=1,5 и N=1, т.е. при логической 1, представленной тремя полупериодами сигнала с частотой F1 внутри одного бита и двумя полупериодами частоты F2 внутри бита для логического 0. При этом согласно полученному выше выражению набег фазы на протяжении одного бита составит: для логической 1- Δφ = +π/2; для логического 0: Δφ= - π/2. Такой случай частотной манипуляции называется манипуляцией с минимальным сдвигом (имеется в виду минимальный сдвиг фазы) - способ MSK (Minimum Shit Keying).
Сформировать сигналы при частотной манипуляции можно с помощью процессора по специальной программе. При этом может быть получен квазисинусоидальный сигнал, представленный из ступенек (рис3.36.).
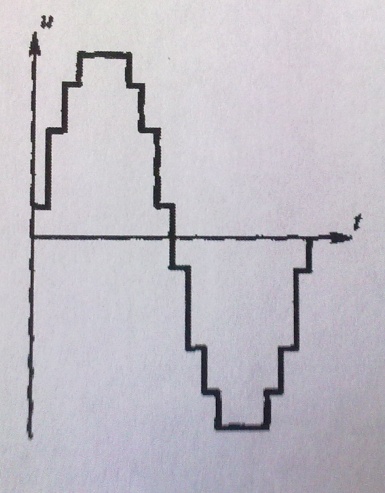
Рис.3.36. Квазисинусоидальный сигнал, составленный из ступенек.
При ЧМ, как и при квадратурной ФМ, можно попарно передавать биты, используя при этом четыре значения частоты, и тем самым вдвое увеличить объем информации.
Контрольные вопросы 1. В чем состоят отличия частотной и фазовой модуляции при передаче дискретных сообщений?








