Передаточные и переходные функции
Лекция 5
Передаточные и переходные функции
1. Передаточные функции по управлению и возмущению
Пусть имеется некоторая САР, схема которой показана на рисунке.
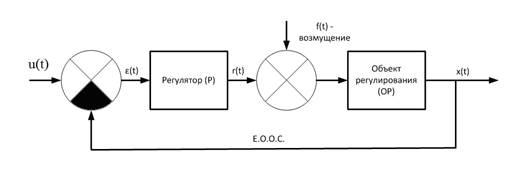
Для данной системы известно следующее:
1. 
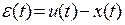– функция рассогласования
2. 
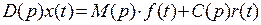
3. Описание регулятора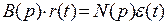 
Используя преобразование Лапласа (при нулевых Н.У.), получаем систему алгебраических уравнений
(*)
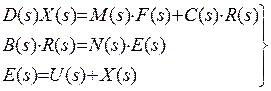Для решения данной системы дифференциальные уравнения, описывающие поведение САР, должны быть заданы. Порядок решения системы (*):
а) исключая из (*) R(s), E(s), разрешаем СУ относительно X(s)
(**)
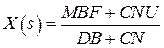б) исключая из (*) R(s), X(s), разрешаем СУ относительно E(s)
(***)
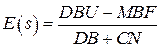Разделим (**) и (***) на DB:
(****)
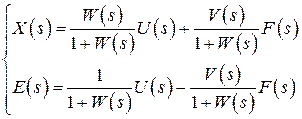где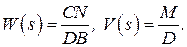 
Первые выражения в (****) характеризуют собой эффект управляющего воздействия (на выходную величину и функцию рассогласования), а вторые – эффект возмущающего воздействия.
Обозначим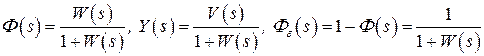 
.
Рассмотрим частные случаи замкнутой САР:
1) 
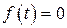(нет помех)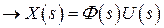 
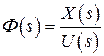- передаточная функция замкнутой САР по управлению
2) 
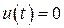(нет входного воздействия)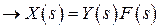 
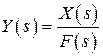- передаточная функция замкнутой САР по возмущению
3) 
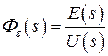- передаточная функция ошибки по управлению
Рассмотрим разомкнутую САР. В (*) изменится только последнее уравнение:
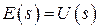
Выход разомкнутой системы
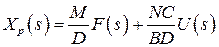
Частные случаи разомкнутой САР:
1) 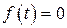(нет помех)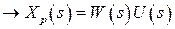 
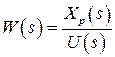- передаточная функция разомкнутой САР по управлению
2) 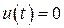(нет входного воздействия)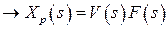 
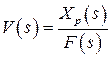- передаточная функция разомкнутой САР по возмущению
2. Переходная функция (временная характеристика)
Переходная функция в отличие от передаточной является функцией вещественной переменной t. Выделяют два типа переходных функций:
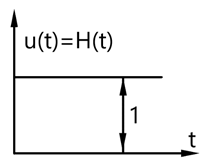
а) переходная функция x(t) – отклик системы (звена, отдельного элемента) при подаче на вход ступенчатой функции H(t)
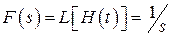
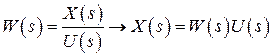
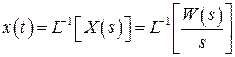
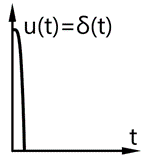
б) импульсная (весовая) переходная функция xи(t) или k(t) – отклик системы (звена, отдельного элемента) при подаче на вход импульсной функции δ(t)
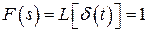
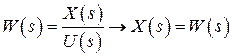
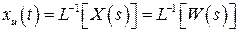
3 основных вида переходных процессов
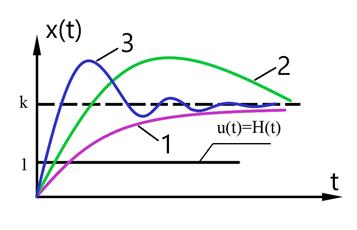
1. Монотонные (1-я производная не меняет знак)
2. Апериодические (смена знака есть, но нет периодичности)
3. Колебательные (производная меняет знак периодически)
Примеры передаточных и переходных функций для различных звеньев
Элементарное звено – отдельный элемент системы, обладающий следующими свойствами:
· Однонаправленное действие (вход нельзя поменять местами с выходом)
· Описывается ДУ не выше 2-го порядка
· Как правило, не может быть представлен в более элементарном виде (есть исключения)
1. Звено нулевого порядка (усилительное)
Рычаг (пример)
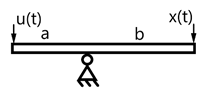
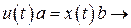
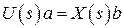
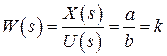
Характеризуется одним параметром – коэффициентом усиления.
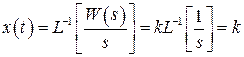
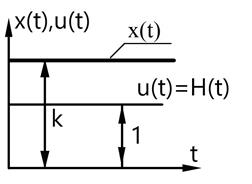
Переходный процесс происходит МГНОВЕННО!
2. Интегрирующее звено (интегратор)
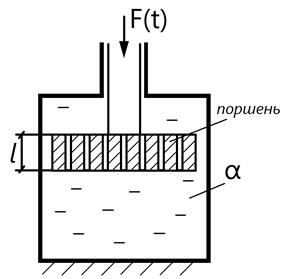
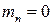- масса поршня,
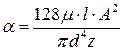- вязкое трение,
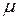- коэффициент динамической вязкости жидкости,
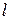- длина отверстия в поршне,
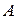- площадь поршня,
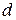- диаметр отверстий,
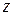- количество отверстий
Уравнение движения поршня
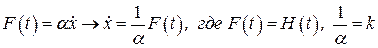
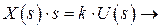
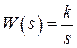
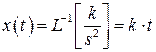
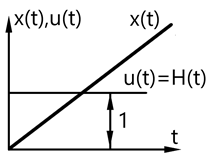
! Нет понятия стационарного состояния системы, что опасно (переходный процесс не устанавливается).
3. Неколебательное звено 2-го порядка
Рассмотрим аналогичное 2-му звено, но при условии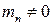 
. Тогда уравнение движения поршня примет вид
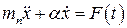
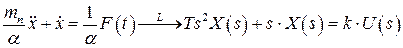
где 
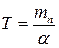- постоянная времени демпфера.
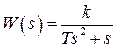
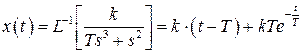
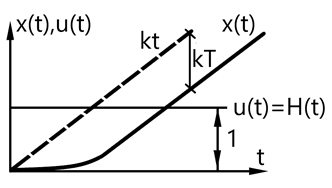
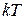- отставание по фазе от звена с безмассовым поршнем.
4. Инерционное звено 1-го порядка (апериодическое)
Рассмотрим аналогичное 2-му звено при условии 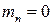, добавив к поршню пружину.
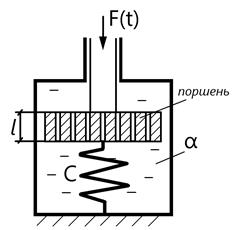
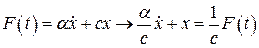
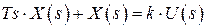, где 
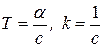
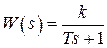
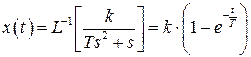
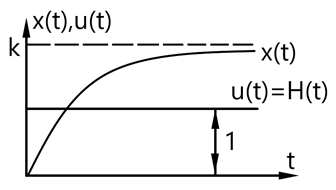
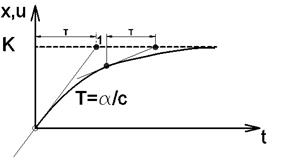
Постоянная времени Т – это величина ПОДКАСАТЕЛЬНОЙ (!). Она const (где бы не провели касательную к графику).
5. Колебательное звено 2-го порядка
Рассмотрим аналогичное 4-му звено, но при условии .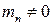
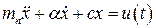
Обозначим
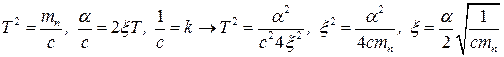
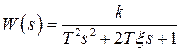
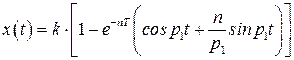
где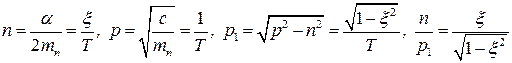 
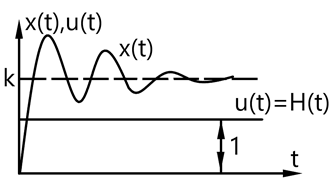
Частный случай. Положим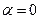 
- вырожденное колебательное звено (консервативное)
,
.
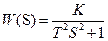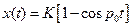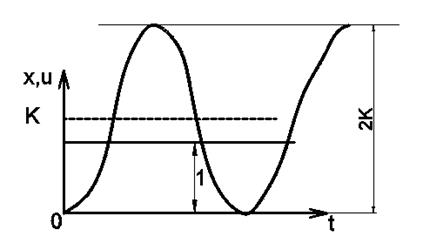
Перерегулирование 100%
Коэффициент динамичности = 2
6. Идеальное дифференцирующее звено
! Абстракция, в реальности не существует.
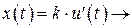
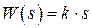
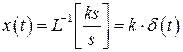
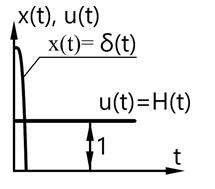
Переходный процесс теоретически происходит мгновенно (фактически – ДО НАЧАЛА ВОЗДЕЙСТВИЯ!! Что естественно в реальности невозможно)