Отметим, что и имеют общих узлов. Кроме того, имеет дополнительных узлов и новые веса . Два правила ( , ) называют парой Гаусса-Кронрода.

Дата: 2025-06-14; Просмотры: 1
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

Таблица весов для пары Гаусса-Кронрода (7,15) для отрезка .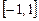

Узлы 7-точечтого правила Гаусса Веса

 

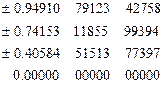
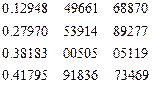
Узлы 15-точечтого правила Крондора Веса

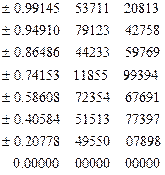
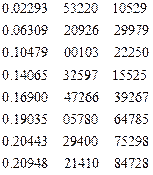
Оценка погрешности правила Гаусса-Кронрода

.

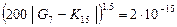Пара Гаусса-Кронрода вместе с приведенной оценкой погрешности сейчас представляет собой один из самых эффективных методов вычисления интегралов общего вида. Пара ( 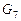, 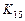) является стандартной.

4.14. Интегрирование таблично заданных функций

Пусть дана последовательность пар чисел

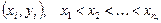
которую мы будем интерпретировать как таблицу точных значений некоторой (неизвестной) функции :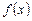

.

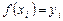Требуется вычислить интеграл

.

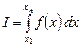К наиболее широко используемым интерполянтам относятся полиномы, кусочно-полиномиальные, и в частности кусочно-линейные функции, эрмитовы кубические функции и сплайны. Кусочно-полиномиальные функции дают наиболее простые квадратурные правила.

Кусочно-линейный интерполянт:

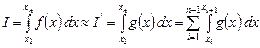
Поскольку функция 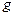линейна на отрезке 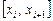, её можно проинтегрировать точно:

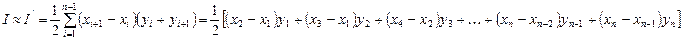. Отметим, что если точки 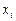расположены на равном расстоянии друг от друга, то мы получим составное правило трапеций, а в случае произвольных 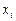- обобщенное правило трапеций.

4.15. Эрмитова кубическая квадратура

Если в качестве интерполянта использовать эрмитову кубическую функцию 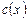, получим

,

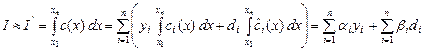где

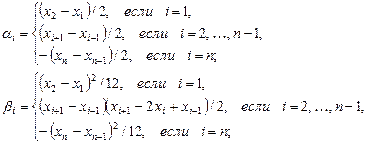
Единственный важный частный случай – это случай равноотстоящих узлов. При этом все 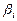, за исключением 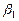и 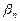, обращаются в нуль, а сумма 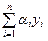становится составным правилом трапеций. Таким образом, приходим к результату:

;

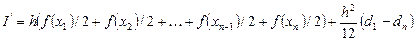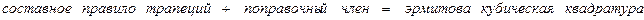
4.16. Двойные и тройные интегралы

Формулы для двух- и трехмерных случаев имеют вид

 

 

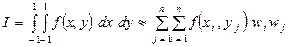
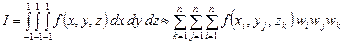
ЛИТЕРАТУРА

  1. Арушанян И.О., Чижонков Е.В. Материалы семинарских занятий по курсу “Методы вычислений” / под ред. Арушаняна О.Б. _ М.: Изд-во ЦПИ при механико-математическом факультете МГУ, 1999.
  2. Бахвалов Н.С. Численные методы. М.: Наука, 1975.
  3. Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. М.: Наука, 1987.
  4. Верлань А.Ф., Сизиков В.С. Интегральные уравнения: методы, алгоритмы, программы. Справочное пособие. Киев: Наукова думка, 1968.
  5. Калиткин Н.Н. Численные методы. М.: Наука, 1978.
  6. Каханер Д., Моулер К., Нэш С. Численные методы и программное обеспечение. М.: Мир, 1998.
  7. Краснов М.Л., Киселев А.И., Макаренко Г.И. Интегральные уравнения. М.: Наука, 1968.
  8. Крылов В.И., Бобков В.В., Монастырный П.И. Вычислительные методы. М.: Наука, 1977.
  9. Forsythe G. E., Malcolm M. A., Moler C. B. Computer Methods for Mathematical Computations. Prentice-Hall, 1977.

10. Форсайт Дж., Малькольм М., Моулер К. Машинные методы математических вычислений / Пер. с англ. М.: Мир, 1980.177с.

  1. Справочник по специальным функциям: Пер. с англ./Под ред. М. Абрамовица и И. Стиган. М.: Наука, 1979.
  2. Ветчинкин В.П. Новые формулы численных квадратур / В.П. Ветчинкин, Ф.М. Коган. – М.; Л.: ОГИЗ. Гос. изд-во технико-теорет. лит., 1949. – 72 с. – Библиогр.: с. 72.

13. Calvetti, D. Computation of Gauss-Kronrod Quadrature Rules [Текст] / D. Calvetti, G.H. Golub, W.B. Gragg, L. Reichel // Mathematics of Computation. – 2000. – V. 69. – No 231. – P.P. 1035-1052.

14. Gander, W. Adaptive Quadrature – revisited [Текст] / W. Gander, W. Gautschi // BIT Numerical Mathematics. – 2000. – V.40. – No 1. – P.P. 84-101.

15. Shampine, L.F. Vectorized Adaptive Quadrature in MATLAB [Текст] / L.F. Shampine // Journal of Computational and Applied Mathematics. – 2008. – V. 211. – P.P. 131–140.

16. Бахвалов, Н. С. Численные методы [Текст] / Н. С. Бахвалов, Н. П. Жидков, Г. М. Кобельков. – М.: Бином. Лаборатория знаний. – 2003.

17. Кронрод, А.С. Узлы и веса квадратурных формул: Шестнадцатизначные таблицы [Текст] / А.С. Кронрод. – М.: Наука. – 1964.

18. Крылов, В.И. Приближённое вычисление интегралов [Текст] / В.И. Крылов. – М.: Наука. – 1967.

19. Суетин, П.К. Классические ортогональные многочлены [Текст] / П.К. Суетин. – М.: Наука. – 1979.