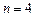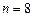Говорят, что -точечное квадратурное правило имеет алгебраическую степень точности , если его остаток равен нулю для любого полинома степени , но не равен нулю для некоторого полинома степени .

Дата: 2025-06-14; Просмотры: 1
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

Алгебраическая степень точности правил трапеций и прямоугольников равна 1 . Алгебраическая степень точности правила Симпсона равна 3.

Квадратурные правила редко используются для интегрирования полиномов, но разумно предположить, что чем больше алгебраическая степень точности квадратурного правила, тем оно лучше. Поэтому правилам высокой алгебраической степени точности отдается предпочтение, хотя на практике часто более важным являются особенности стратегии применения правила, а не оно само.

Если проинтегрировать лагранжев интерполяционный полином 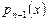, проходящий через точки 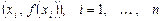, то придём к правилу

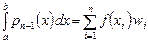, где .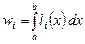

Правила такого типа называются интерполяционными. Наиболее известные квадратурные правила получаются, если выбрать точки равноотстоящими на отрезке интегрирования; такие правила называются правилами Ньютона-Котеса. Правила трапеций и Симпсона представляют собой правила Ньютона-Котеса невысоких алгебраических степеней точности. Правила же Ньютона-Котеса, алгебраическая степень точности которых высока, обладают, к сожалению, тем свойством, что среди их весов имеются отрицательные. Обычно это не желательный эффект, поскольку интегрирование положительной функции может привести к искажению результата из-за катастрофической потери значащих разрядов.

Получим квадратурную формулу Гаусса на произвольное число узлов

,

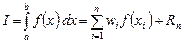в которой 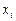ни ни 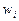заранее не предписаны, а выбираются таким образом, чтобы правило было точным для полиномов наиболее высокой степени. Для любого 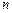существует единственная квадратурная формула Гаусса. Её алгебраическая степень точности равна 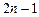, причём 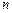-точечной формулы большей алгебраической степени точности не существует. В этом смысле формула Гаусса является наилучшей.

Если 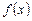имеет 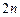непрерывных производных на 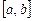, то

.

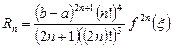Относительно 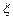известно лишь, что .

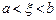Правила Гаусса принадлежат к наиболее часто применяемым правилам на практике.

Перечислим их свойства.

1. За небольшим исключением, веса и узлы правил Гаусса иррациональны. При 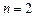, веса 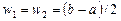. Кроме того, если 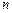нечётно, то один из узлов совпадает с серединой отрезка интегрирования .

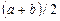2. Правила Гаусса относятся к правилам открытого типа. Это означает, что ни один из узлов не совпадает ни с одним из концов отрезка интегрирования 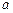или .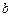

3. Множества узлов двух правил Гаусса почти не пересекаются. Иными словами, узлы 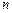-точечного правила отличается от узлов 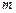-точечного правила. Исключение состоит в том, что если 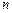нечётно, то один из узлов совпадает с серединой отрезка интегрирования.

4. Вывод правил Гаусса позволяет предположить, что если подынтегральная функция близка к полиному, то правило Гаусса наиболее пригодно для вычисления интеграла от такой функции.

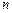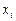
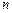5. Правила Гаусса являются интерполяционными. Это означает, что если мы возьмём узлов -точечной формулы Гаусса и 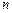соответствующих значений 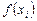и построим тот единственный полином степени 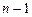, который интерполирует эти данные, то интегрирование по отрезку 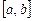построенного полинома даст нам тот же результат, что и применение к 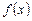формулы Гаусса.

6. Существует тесная связь между квадратурами Гаусса и ортогональными полиномами. Узлы 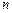-точечного правила Гаусса являются нулями полинома Лежандра степени 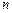. Из-за этого эти квадратуры часто называют также квадратурами Гаусса-Лежандра.

Некоторые квадратуры Гаусса для интеграла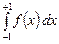

Узлы Веса

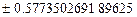
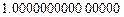
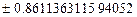
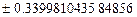
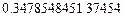
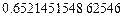
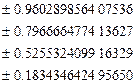
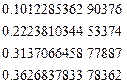
4.12. Переход от одного отрезка к другому

Программы, в которых реализованы квадратурные правила, обычно позволяют задавать концы отрезка интегрирования произвольно . Однако в таблицах, правила приведены для какого-либо определенного отрезка, чаще всего 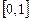или 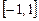. Приближенное значение интеграла 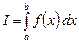для какого-либо другого отрезка 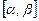будет иметь вид .

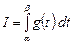В этом случае нужно с помощью замены переменной осуществить переход от переменной 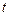, принадлежащей отрезку 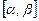( где возможно 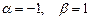) к переменной 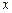, принадлежащей отрезку 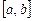. Тогда формула примет вид

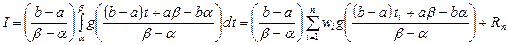
Для отрезка 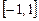она упростится

.

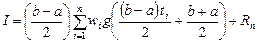Существует много преобразований при переходе от переменной 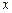к переменной 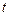и преобразовании отрезка 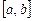к отрезку 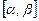, но приведенное выше – самое простое в силу своей линейности.

4.13. Квадратурные правила Гаусса-Кронрода

Вычисление определённых интегралов находит широкое применение как в математических, так и в прикладных задачах. На практике, как правило, используют приближённые квадратурные формулы. Одной из наиболее известных и востребованных при разработке пакетов компьютерной математики (MATLAB, Mathematica) является квадратурная формула Гаусса-Кронрода [1-6].

При построении квадратурных формул типа Гаусса-Кронрода используются различные системы ортогональных многочленов [1-4, 6]. Рассмотрим систему ортогональных многочленов Якоби 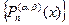. Нетрудно доказать следующее свойство симметрии этих многочленов.

ТЕОРЕМА. Для многочленов Якоби 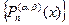, ортогональных на 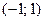с весовой функцией 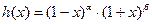( 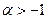, 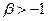), выполняется .

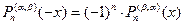Для весовой функции вида 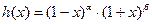при 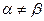эта теорема обобщает доказанное в [7] утверждение (Теорема 1.3).

В настоящей работе показано, что для базовой формулы типа Гаусса (построенной с помощью многочленов Якоби), используя указанное свойство симметрии, можно построить две парные симметричные квадратурные формулы типа Гаусса-Кронрода.

Не теряя общности, будем рассматривать промежуток интегрирования 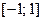. Пусть построена базовая квадратурная формула типа Гаусса

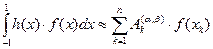, (1)

где весовые коэффициенты 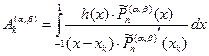, 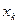– нули многочлена Якоби с единичным старшим коэффициентом 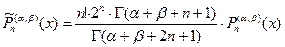. Тогда по найденным значениям весовых коэффициентов и узлам 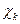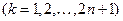можно построить две парные симметричные формулы типа Гаусса-Кронрода (равного алгебраического порядка точности):

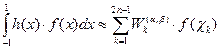, (2)

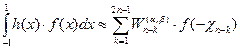, (3)

где 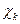– нули полинома Кронрода 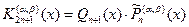, который строится по аналогии с методом, изложенным в [4]. Коэффициенты многочлена 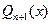определяются с помощью взвешенных степенных моментов 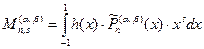по формулам

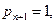
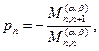
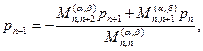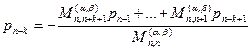… , а весовые коэффициенты вычисляются по формуле .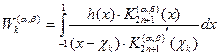

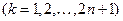Заметим, что правые части в формулах (2) и (3) в общем случае при 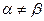дают различные приближенные значения интеграла, а при 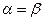– равные. Получение двух приближенных значений интеграла с помощью одного набора весовых коэффициентов 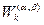и узлов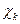 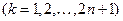дает определенные вычислительные и алгоритмические преимущества при использовании формул (2) и (3).

В [4] указано, что формулы (1) и (2)–(3) при некоторых ограничениях на весовую функцию можно применять при вычислении интегралов вида 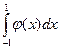, предварительно выделив весовую функцию и положив .

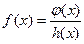В 1965 году задачу получения оценок погрешности квадратурных правил Гаусса исследовал советский специалист в области вычислительной математики А. С. Кронрод. Идея Кронрода состояла в построении, наряду с правилами Гаусса, нового правила, узлами которого были бы как все узлы правила Гаусса ( 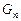), так и некоторые другие точки. Кронрод предложил строить правила вида

.
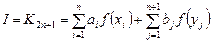