{Вычисление определенного интеграла по формуле Симпсона}

Дата: 2025-06-14; Просмотры: 1
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

Uses CRT;

{Глобальные переменные}

Type

RealType = Extended; {базовый вещественный тип}

FunType = Function(x : RealType) :RealType;

Var

A, B, Int : RealType;

N : Integer;

{$F+}

Function Fun(x : RealType) : RealType;

{Заданная подинтегральная функция}

Begin

Fun:= Cos(x*x);

End; {Fun}

{$F-}

Function Simpson(Fun : FunType;

A, B : RealType; N : Integer) : RealType;

{Вычисление определенного интеграла по формуле Симпсона}

{

ВОДНАЯ ИНФОРМАЦИЯ:

Fun - подынтегральная функция;

A, B - границы интервала интегрирования;

N - количество подынтервалов, на которые разбивается

интервал интегрирования.

ВЫХОДНАЯ ИНФОРМАЦИЯ:

Simpson - значения этой функции есть вычисленный по

формуле Симпсона определенный интеграл.

}

Var

h, I : RealType;

k : Integer;

Begin {Simpson}

h:= (B-A)/(N*2.0);

I:= Fun(A);

For k:= 1 to (2*N-1) do

If Odd(k) then {Проверка k на нечетность}

I:= I + 4.0 * Fun(A+k*h)

else

I:= I + 2.0 * Fun(A+k*h);

Simpson:= (I + Fun(B)) * h / 3.0

End; {Simpson}

{Головная программа}

BEGIN

ClrScr;{Очищает экран, модуль Crt}

WriteLn (' ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА МЕТОДОМ СИМПСОНА');

WriteLn;

WriteLn (' ИСХОДНОЕ УРАВНЕНИЕ: y = Cos(x*x)');

WriteLn('Введите исходные данные:');

Write('Начало интервала интегрирования A= '); ReadLn(A);

Write('Конец интервала интегрирования B= '); ReadLn(B);

Write('Количество интервалов разбиения N= '); ReadLn(N);

WriteLn;

Int:= Simpson(Fun, A, B, N);

WriteLn (' **************** РЕЗУЛЬТАТ ****************');

WriteLn(' Значение интеграла: ',Int:12:10);

WriteLn;

WriteLn(' ДЛЯ ПРОДОЛЖЕНИЯ НАЖМИТЕ ЛЮБУЮ КЛАВИШУ!!!');

Repeat Until KeyPressed; {Ожидает нажатия любой клавиши, модуль Crt}

ClrScr;{Очищает экран, модуль Crt}

END.

4.7. Формула Ньютона-Котесса при n=4 (формула Бодэ)

Численное интегрирование методом Ньютона-Котеса при 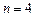(формула Боде):

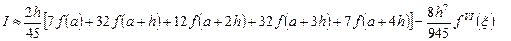
4.8. Формула Уэддля (Веддля)

Метод Уэддля (Веддля) базируется на применении к каждому из 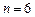отрезков разбиения 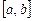формулы

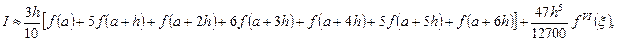
Метод применяют в частном случае, когда 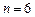. Это метод пятого порядка для шести точек.

4.9. Формула Ньютона-Котесса (n=6)

Формула с повышенной точностью (в сравнении с формулой Уэддля) для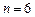

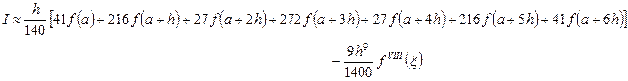
метод седьмого порядка для шести точек.

4.10. Метод Чебышева

Метод основан на вычислении определенного интеграла по формуле

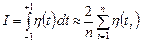
Этот интеграл приводится к виду

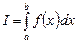
подстановкой

.

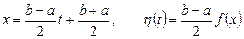Выбор значений 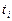производится из условия, что формула интегрирования будет точной для 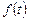вида, 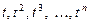, т. е. для полиномом вплоть до 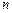-й степени.

Для ,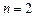

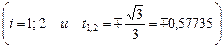для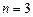

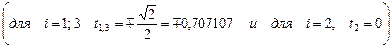
Формула точна для полинома степени .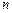

4.11. Метод Гаусса