4.2. Одномерные квадратурные правила и формулы.. 4
Лекции
«ОСНОВНЫЕ ЧИСЛЕННЫЕ МЕТОДЫ,
ПРИМЕНЯЕМЫЕ В ЭЛЕКТРОТЕХНИЧЕСКИХ ЗАДАЧАХ»
(Часть IV : Численные квадратуры)
Новочеркасск 2012
СОДЕРЖАНИЕ
СОДЕРЖАНИЕ.. 3
4. ЧИСЛЕННЫЕ КВАДРАТУРЫ... 4
4.1. Введение. 4
4.2. Одномерные квадратурные правила и формулы.. 4
4.3. Формулы прямоугольников. 4
4.4. Формула трапеций. 5
4.5. Метод Ньютона-Котесса. 6
4.6. Формула Симпсона (метод парабол) 6
4.7. Формула Ньютона-Котесса при n=4 (формула Бодэ) 8
4.8. Формула Уэддля (Веддля) 8
4.9. Формула Ньютона-Котесса (n=6) 8
4.10. Метод Чебышева. 8
4.11. Метод Гаусса. 8
4.12. Переход от одного отрезка к другому. 10
4.13. Квадратурные правила Гаусса-Кронрода. 10
4.14. Интегрирование таблично заданных функций. 13
4.15. Эрмитова кубическая квадратура. 13
4.16. Двойные и тройные интегралы.. 14
ЛИТЕРАТУРА.. 15
4. ЧИСЛЕННЫЕ КВАДРАТУРЫ
4.1. Введение
Этот раздел посвящён решению следующей задачи: вычислить интеграл
.
Это одна из фундаментальных задач математического анализа. Она тесно связана с задачей решения дифференциальных уравнений.
4.2. Одномерные квадратурные правила и формулы
Обычно аппаратом, используемым для построения квадратур, является аппарат интерполирования. Вместо того, чтобы вычислить непосредственно, сперва вычисляют значения функции 
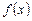в заданных точках 
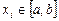. Пусть 
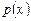- интерполяционный полином, проходящий через точки 
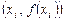. Тогда, если 
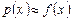, то и 
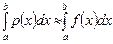. Поскольку интерполирование полинома не составляет труда, а аппарат интерполирования вполне доступен, такой подход представляется численно реализуемым и эффективным.
Получим простейшие квадратурные формулы. Для этого введём терминологию , которой в дальнейшем будем пользоваться. Назовём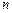 
-точечной квадратурной формулой равенство 
.
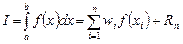При этом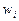 
называются весами, а 
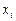- узлами квадратурной формулы, 
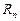- остатком или погрешностью. Веса и узлы зависят от 
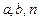, но не зависят от 
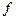. Сумму в правой части, которую можно рассматривать как приближение к 
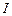, часто называют квадратурным правилом. Чтобы приближенно вычислить интеграл, мы вычисляем только квадратурное правило, так как остаток обычно содержит выражение нам недоступные (производные подынтегральной функции). Важное свойство наших формул – их линейность. Это означает, что правило, дающее приближение к интегралу от 
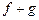, можно получить сложением правил, дающих приближение к 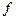и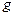 
.
4.3. Формулы прямоугольников
Простейшие методы из класса методов Ньютона-Котеса, когда подынтегральную функцию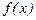 
на интервале интегрирования заменяем полиномом нулевой степени, т. е. константой. Подобная замена является неоднозначной, так как константу можно выбрать равной значению подынтегральной функции в любой точке интервала интегрирования. Приближенное значение интеграла определится как площадь прямругольника, одна из сторон которого есть длина отрезка интегрирования, а другая – аппроксимирующая константа. Отсюда происходит и название методов.
Наименьшую погрешность из методов прямоугольников имеет метод средних прямоугольников, когда константу берём равной значению 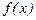в средней точке 
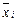интервала 
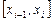(Рис.1 а).
Методы левых (Рис.1 б) и правых (Рис.1 в) прямоугольников, заменяющих интеграл нижней и верхней суммами Дарбу, имеют сравнительно невысокую точность.
Для метода средних прямоугольников
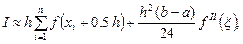
где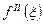 
- значение второй производной 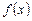в точке 
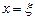, где она максимальна, 
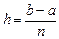- шаг интегрирования, 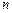- количество отрезков разбиения.
Для метода левых прямоугольников
.
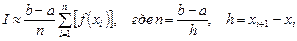Для метода правых прямоугольников
.
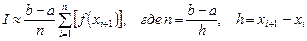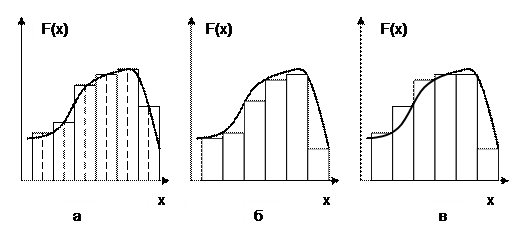
Рис. 1. Методы средних (а), левых (б) и правых (в) прямоугольников.
Для метода прямоугольников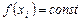 
на отрезке интегрирования.
4.4. Формула трапеций
Если подынтегральную функцию 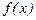заменить полиномом первой степени на участке 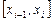, то приближенное значение интеграла определится как площадь трапеции:
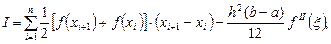
где 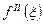- значение второй производной 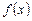в точке 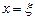, где она максимальна, 
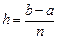- шаг интегрирования, 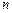- количество отрезков разбиения.
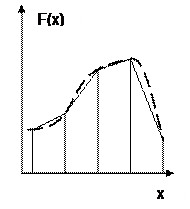
Рис. 2. Метод трапеций.
Метод трапеций, как и метод средних прямоугольников, имеет второй порядок.
Составная квадратурная формула трапеций для случая, когда точки 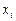расположены на равном расстоянии друг от друга, для шага (длины элементарного отрезка) 
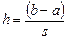при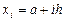 
на каждом отрезке 
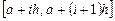имеет вид:
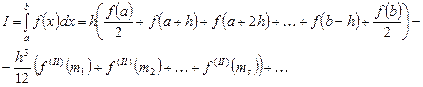
Или
,
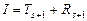где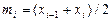 
. На практике используют только 
.
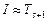Если подынтегральная функция задана аналитически, то предпочтительнее из методов второго порядка применять метод средних прямоугольников вследствие его меньшей погрешности.
4.5. Метод Ньютона-Котесса
Метод основан на интерполяции 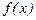в 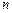пормежутках полиномом Лагранжа. В общем случае 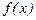должна задаваться 
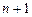ординатами. Формулы интегрирования точны, если 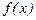- многочлен 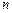-й степени. При 
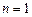получаем метод трапеций.
4.6. Формула Симпсона (метод парабол)
Этот метод является частным случаем метода Ньютона-Котесса при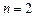 
.
Если подынтегральную функцию 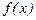заменить полиномом второй степени на участке 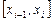, то приближенное значение интеграла определится как площадь под параболой или формулой Симпсона:
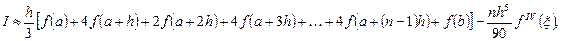
где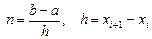 
.
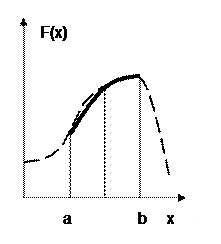
Рис. 3. Метод Симпсона (парабол).
Выражение для остаточного члена показывает, что формула Симпсона точна, даже если 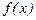- многочлен третьей степени (погрешность трёхточечного правила Симпсона равна нулю, если 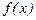-кубический полином). Эта частная особенность формулы Симпсона объясняет её преимущественное применение.
Формулой Симпсона называется интеграл от этого полинома на отрезке [a, b]:
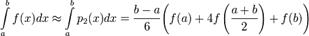
Метод Симпсона имеет порядок погрешности 4 и алгебраический порядок точности 3.
Погрешность при интегрировании по отрезку [a,b] с шагом h определяется по формуле:
,
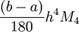где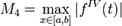 
— максимум четвёртой производной функции.
Так же, при невозможности оценить погрешность с помощью максимума четвертой производной (например, на заданном отрезке она не существует, либо стремится к бесконечности), можно использовать более грубую оценку:
,
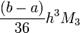где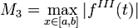 
— максимум третьей производной функции.
Пример.
{$N+,E+,F+}
PROGRAM Integral;