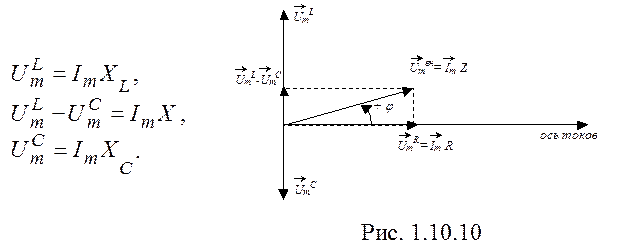Таким образом, напряжение на индуктивности и емкости изменяются в противофазе.

Дата: 2025-05-25; Просмотры: 3

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Для контура в любой момент времени напряжения U^R, U^L и U^C в сумме должны быть равны приложенному напряжению U_{внешнее}.

Каждое из напряжений U^R, U^L и U^C совершает гармонические колебания и, следовательно, может быть представлено с помощью вектора амплитуды. Сложив векторы амплитуды, изображающие напряжения U^R, U^L и U^C, получим вектор, изображающий амплитуду внешнего напряжения:

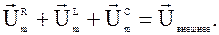(1.10.17)

Проведем суммирование с помощью диаграммы
ток-напряжение (рис. 1.10.10) для момента времени t = 0.

Длина результирующего вектора 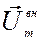равна амплитуде колебаний внешнего напряжения 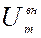. Направление результирующего вектора образует с осью токов угол j, равный сдвигу фаз:

t g j =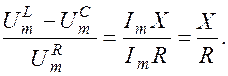

Модуль результирующего вектора 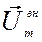можно определить по теореме Пифагора:

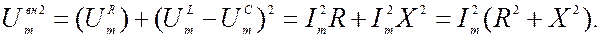
Отсюда получаем

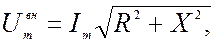
где X-реактанс контура, определяемый формулой (1.10.11).

Полное сопротивление контура Z определим по закону Ома:

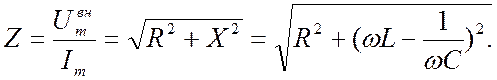
Амплитуда силы тока в последовательном контуре равна

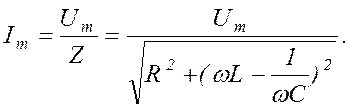
Таким образом, с помощью диаграммы
ток-напряжение мы получили те же значения I_m, U_m и Z, что и при решении уравнения вынужденных колебаний (1.9.11-1.9.13).

§1.11. Мощность, выделяемая в цепи

переменного тока

Мгновенное значение мощности, выделяемой в цепи P(t), определяется формулой

P(t) = I(t)U(t) = I_mcos( w t - j )U_mcos w t.

Для преобразования последнего уравнения воспользуемся тригонометрической формулой

cos a cos b =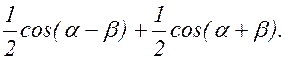

После тригонометрических преобразований получаем:

P(t) = 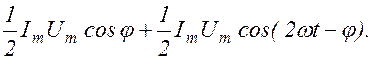(1.11.1)

В разные моменты времени значение P(t) имеет различную величину, в частности, оно будет равно нулю в те моменты, когда равны нулю либо ток, либо напряжение.

Практический интерес представляет среднее значение мощности, выделяемой за период. Усредним (1.11.1) по времени за период:

< P(t) > =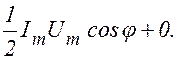

Нуль получился в результате того, что среднее значение cos(2 w t - j ) за период равно нулю, поскольку косинус принимает за период T так же часто положительные значения, как и равные им отрицательные.

Таким образом:

<P(t)> = 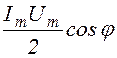, (1.11.2)

где множитель cos j называют коэффициентом мощности. Значение cos j можно определить из диаграммы ток-напряжение (рис. 1.10.10):

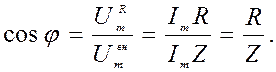(1.11.3)

Подставляя значение cos j в формулу (1.11.2), получаем

<P(t)> =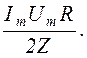

Учитывая, что 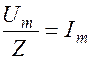, можем записать выражение для мощности в виде

<P(t)> = 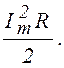(1.11.4)

Такую же мощность выделяет постоянный ток силой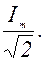

Эквивалентный постоянному току по мощности переменный ток называют действующим или эффективным значением силы тока:

I _Эфф. = 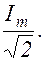(1.11.5)

Аналогично определяют действующее (или эффективное) значение напряжения:

U _Эфф = 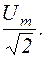(1.11.6)

С учетом (1.11.5) и (1.11.6) формулу (1.11.2) можно записать в виде

<P(t)> = I _Эфф U _Эфф с os j . (1.11.7)

Из формулы (1.11.4) следует, что количество тепла, выделяемое в цепи переменного тока, выражается известной формулой Джоуля-Ленца, если под силой тока понимать I_эфф:

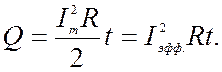(1.11.8)

Анализ формулы (1.11.8) показывает, что тепло Q выделяется только на активном сопротивлении. Индуктивное сопротивление X_L и емкостное X_C никакой роли в процессе выделения тепла не играют. Поэтому реактивные сопротивления иногда называют безваттными сопротивлениями. Этот вывод можно сделать и из рассмотрения векторных диаграмм ток-напряжение, представленных на рисунках 1.10.4 и 1.10.5. В этих случаях,

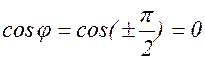и <P(t) > = 0.