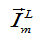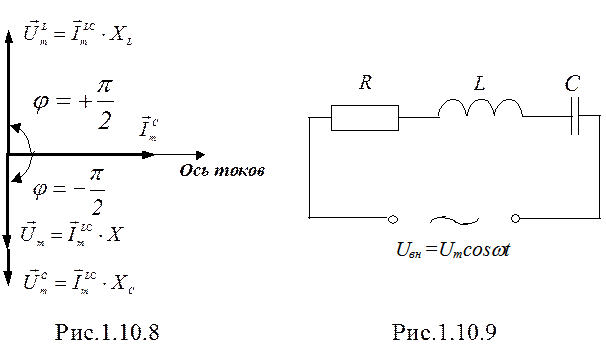§1.10. Расчет цепей переменного тока методом диаграмм ток-напряжение
Установившиеся вынужденные колебания можно рассматривать как протекание в цепи переменного тока I=Im( w )cos( w t- j ), обусловленного переменным напряжением:
u внешнее = Um cos w t.
Ток по отношению к напряжению сдвинут на угол j, определяемый формулой (1.9.15). Сдвиг фаз между током и напряжением становится особенно наглядным, если изображать амплитуды токов и напряжений с помощью векторов.
I. Рассмотрим цепь, содержащую только активное сопротивление R (C ® ¥ , L=0) (рис.1.10.1).
Величина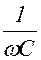 
=0. Следовательно, tg j, определяемый формулой (1.9.15), равен нулю и j = 0.
Таким образом, ток и напряжение на активном сопротивлении изменяются в фазе. Амплитуда тока, определяемая формулой (1.9.11), в данном случае равна
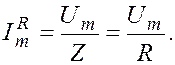(1.10.1)
Отсюда получаем амплитуду падения напряжения на сопротивлении:
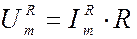. (1.10.2)
Выберем произвольное направление, которое назовем осью токов. Отложим вдоль него вектор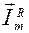 
Так как j = 0, то вектор 
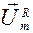будет совпадать с ним по направлению (рис.1.10.2).
 |
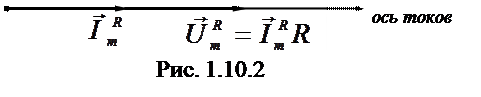II. Рассмотрим цепь, содержащую только индуктивность L (R=0, C= ¥) (рис.1.10.3).
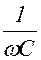В этом случае R = 0, = 0. Из формулы (1.9.15) следует, что tq j = ¥, значит 
.
|
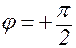Согласно (1.9.14) сила тока через индуктивность изменяется по закону:
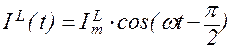. (1.10.3)
Таким образом, ток на индуктивности отстает от напряжения по фазе на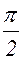 
. Это объясняется тем, что нарастанию тока препятствует ЭДС самоиндукции, возникающая в катушке при колебаниях силы тока.
Амплитуда тока через индуктивность равна
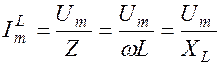, (1.10.4)
где XL= w L. (1.10.5)
Величину XL= w L называют реактивным индуктивным сопротивлением. При w = 0, XL = 0, то есть постоянному току индуктивность сопротивления не оказывает.
Амплитуда падения напряжения на индуктивности определяется формулой
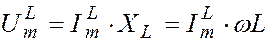. (1.10.6)
Построим диаграмму ток-напряжение для индуктивности (рис. 1.10.4).
Отметим, что на диаграмме j > 0, если поворот от вектора амплитуды тока к вектору амплитуды напряжения осуществляется против часовой стрелки.
III. Рассмотрим цепь, содержащую только емкость С (R= 0, L= 0), (рис. 1.10.5).
 |
|
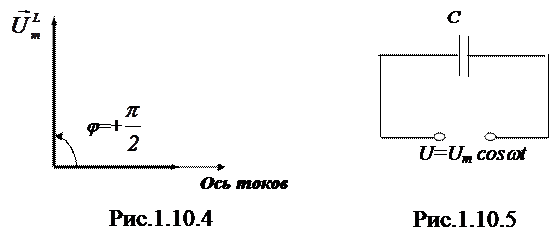Из формулы (1.9.15) следует, что tq j = - ¥, а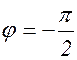 
.
Закон изменения тока через емкость имеет вид
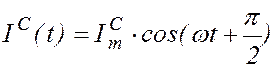. (1.10.7)
Таким образом, ток на емкости опережает напряжение по фазе на .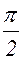
Амплитуда тока на емкости определяется формулой
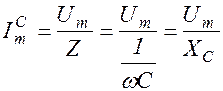, (1.10.8)
где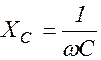 
. (1.10.9)
Величину XC называют реактивным емкостным сопротивлением. При w = 0 емкостное сопротивление обращается в бесконечность, это значит, что постоянный ток через конденсатор не проходит.
Амплитуда падения напряжения на конденсаторе определяется формулой
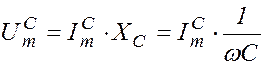. (1.10.10)
Диаграмма ток-напряжение на емкости имеет вид
(рис. 1.10.6):
 |
IV. Рассмотрим цепь, состоящую из последовательно соединенных емкости C и индуктивности L (R=0) (рис.1.10.7).
Для этой цепи tq j =± ¥, следовательно, сдвиг фаз между током и напряжением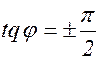 
.
В этом случае ток либо опережает, либо отстает по фазе от напряжения.
Результат зависит от знака величины:
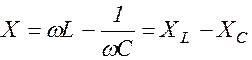. (1.10.11)
Величину X, определяемую формулой (1.10.11), называют реактивным сопротивлением или реактансом цепи. Сила тока в цепи изменяется по закону:
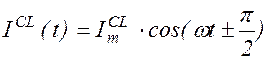. (1.10.12)
Амплитуда силы тока равна
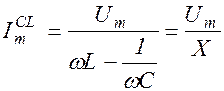. (1.10.13)
Векторная диаграмма ток-напряжение для последовательно соединенных L и C изображена на рис.1.10.8.
V. Рассмотрим цепь, представляющую собой последовательный R, L, C контур (рис.1.10.9).
|
При установившихся колебаниях в контуре протекает ток:
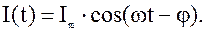
Между током и приложенным напряжением есть сдвиг фаз, определяемый выражением:
.
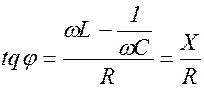Падение напряжения на отдельных элементах контура в каждый момент времени можно выразить по закону Ома:
UR (t)=RI(t) =RImcos( w t - j )=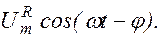 
(1.10.14)
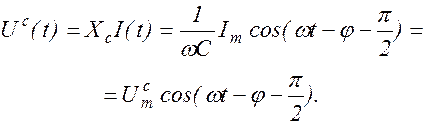(1.10.15)
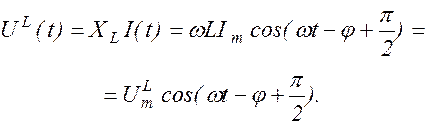(1.10.16)
В формулах (1.10.14-1.10.16) учтено, что на активном сопротивлении ток и напряжение изменяются в фазе, напряжение на емкости отстает по фазе от силы тока на 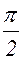, а на индуктивности опережает ток на .
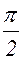Из (1.10.15) и (1.10.16) определим разность фаз между напряжением на емкости и индуктивности в любой момент времени:
Δψ = w t - j + 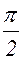- w t + j + 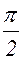= p .