Следовательно, логарифмический декремент затухания обратен числу колебаний Ne, которые система совершит, прежде чем амплитуда колебаний уменьшится в e раз.

Дата: 2025-05-25; Просмотры: 4
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

Логарифмический декремент l определяется параметрами контура: R, L, C.

Если затухание мало (b 2 « w 0 2), то .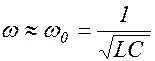

В этом случае справедливо:

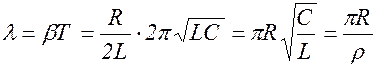, (1.8.13)

где r - волновое сопротивление контура.

Одной из важнейших характеристик колебательного контура является его добротность D, которая характеризует способность колебательной системы поддерживать созданные в ней колебания. Добротность прямо пропорциональна числу колебаний, совершенных за время жизни:

D= 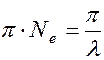. (1.8.14)

При малом затухании, подставив вместо l выражение (1.8.13), получим

D= 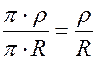. (1.8.15)

Можно показать, что при незначительном затухании добротность контура D пропорциональна отношению энергии Е, запасенной в контуре в данный момент, к убыли этой энергии (ΔЕ) за один период колебания:

D=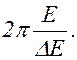

Период Т затухающих колебаний в реальном контуре определяется формулой

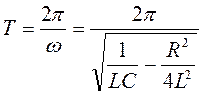. (1.8.16)

С увеличением сопротивления контура период возрастает и при значении Rкр=2 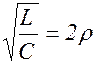обращается в бесконечность.

Это значение называется критическим сопротивлением контура.

Таким образом, в реальном колебательном контуре при наличии свободных колебаний могут реализоваться три режима:

I) при R>2 r – апериодический (режим срыва колебаний). В этом случае изменение заряда на обкладках конденсатора не носит колебательного характера. Решение уравнения (1.8.3) в этом случае имеет вид

 

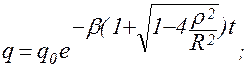(1.8.17)

 

II) R = 2 r - критический режим;

III) R < 2 r - условие малых затуханий, при выполнении этого условия колебания существуют и решение уравнения (1.8.3) имеет вид, определяемый формулой (1.8.4).

§1.9. Вынужденные электрические колебания

 

В реальном колебательном контуре (рис.1.9.1) активное сопротивление R отлично от нуля, и свободные электромагнитные колебания затухают.

 


Рис. 1.9.1

Для получения незатухающих колебаний к контуру необходимо подводить энергию, например, подавая в контур переменное напряжение, меняющееся по гармоническому закону:

u внешнее = Umax cos w t. (1.9.1)

Колебания, совершаемые в системе, находящейся под внешним периодическим воздействием, называются вынужденными.

Запишем для контура второй закон Кирхгофа:

IR + Uc = 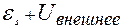. (1.9.2)

Приняв во внимание известные соотношения

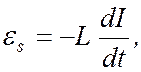
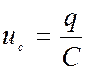и ,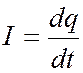

перепишем уравнение (1.9.2) в виде

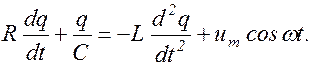
Разделив обе части уравнения на L и учтя ранее принятые обозначения (1.3.5) и (1.8.2), получим дифференциальное уравнение вынужденных колебаний в контуре:

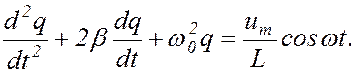(1.9.3)

Решение уравнения (1.9.3) в случае установившихся колебаний имеет вид

q(t) = qm( w )cos[ w t- a ( w )]. (1.9.4)

Таким образом, изменение заряда в контуре со временем представляет собой гармоническое колебание с частотой w , равной частоте внешнего напряжения.

Начальная фаза колебания a(w) определяется соотношением:

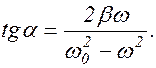(1.9.5)

Амплитуда заряда пропорциональна амплитуде внешнего напряжения и зависит от частоты внешнего воздействия:

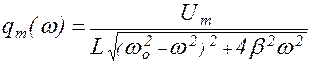. (1.9.6)

Зависимость qm от частоты w приводит к тому, что при некоторой частоте w рез контур оказывается наиболее отзывчивым на внешнее воздействие, и амплитуда заряда достигает максимального значения. Это явление называют резонансом, а частоту w рез называют резонансной частотой.

Напряжение на конденсаторе будет изменяться по закону:

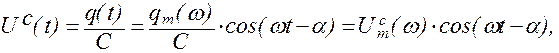(1.9.7)

где 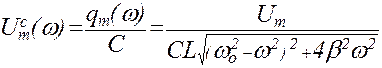. (1.9.8)

Из (1.9.8) следует, что амплитудное значение напряжения на конденсаторе зависит от частоты внешнего воздействия.

Силу тока в контуре найдем, взяв производную по t от выражения (1.9.4):

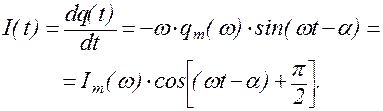(1.9.9)

Из (1.9.9) следует, что амплитудное значение силы тока также зависит от частоты внешнего воздействия и определяется формулой

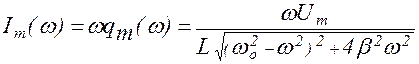. (1.9.10)

Если подставить в (1.9.10) значения 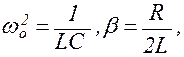то получим

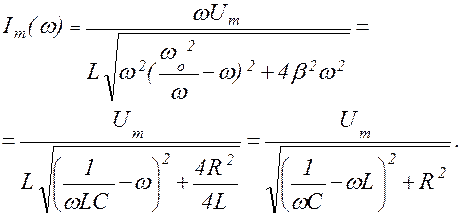(1.9.11)

Уравнение (1.9.11) является законом Ома для переменного тока. Отметим, что это соотношение справедливо только для амплитудных значений тока и напряжения. Из закона Ома следует, что знаменатель в формуле (1.9.11) представляет собой сопротивление контура. Его обозначают Z и называют полным электрическим сопротивлением контура или импедансом.

Таким образом:

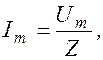(1.9.12)

где 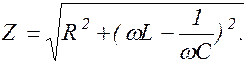(1.9.13)

Выражение (1.9.13) позволяет рассчитать полное сопротивление контура, у которого R, L и C включены последовательно. Обратимся к закону изменения силы тока (1.9.9).

Если ввести обозначение 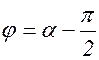, то формулу(1.9.9) можно записать в виде

I(t) =Im( ω )cos( ω t – φ ). (1.9.14)

Из сравнения (1.9.1) и (1.9.14) видно, что φ представляет собой сдвиг фаз между током в контуре и приложенным внешним напряжением.

Из-за сдвига фаз φ закон Ома не справедлив для мгновенных значений силы тока I(t) и напряжения U(t).

Выясним, от чего зависит сдвиг фаз φ. Из обозначения φ= a - 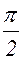следует:

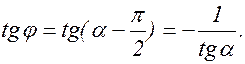
Учитывая формулу (1.9.5) , получаем для tg j выражение:

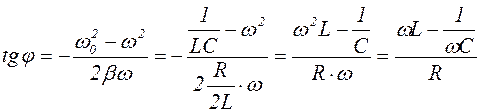. (1.9.15)

Из формулы (1.9.15) следует, что сдвиг фаз в цепи переменного тока определяется соотношением между величинами R, L, C и зависит от частоты внешнего напряжения.

При 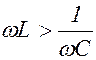сдвиг фаз j > 0. Зависимость силы тока от времени (1.9.14) имеет вид

I=Im( w )cos( w t- j ).

Из сравнения этого выражения с (1.9.1) видно, что ток отстает по фазе от напряжения. При 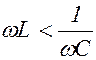сдвиг по фазе между током и напряжением j < 0 и уравнение (1.9.14) имеет вид

I(t)=Im( w )cos( w t+ j ),

то есть ток опережает напряжение (1.9.1) по фазе.