Направление движения по эллипсу определяется знаком разности фаз (рис.1.7.3).

Дата: 2025-05-25; Просмотры: 18
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0
 

 

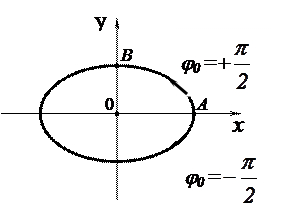Рис. 1.7.3

II. Пусть частоты складываемых колебаний не равны: w 1¹w 2.

В этом случае результирующее колебание происходит по сложной кривой, вид которой определяется разностью фаз и соотношением частот. Эти кривые называются фигурами Лиссажу.

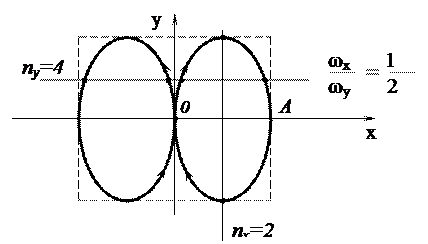На рис.1.7.4 приведена фигура Лиссажу для отношения частот 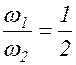и разности фаз j 1 - j 2 = .

 

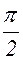Рис. 1.7.4

 

Уравнения складываемых колебаний, соответствующих рис.1.7.4, имеют вид:

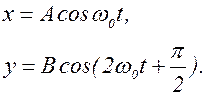(1.7.4)

Фигуры Лиссажу применяют для сравнения частот складываемых колебаний. Отношение 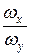равно отношению числа точек пересечения фигуры линиями, перпендикулярными осям ox и oy (рис.1.7.4), т.е.

.

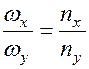§1.8. Свободные затухающие колебания в
электрическом контуре

 

Всякий реальный колебательный контур обладает активным сопротивлением (R ¹ 0), вследствие чего энергия, запасенная в контуре, постепенно расходуется на нагревание и колебания затухают.

 


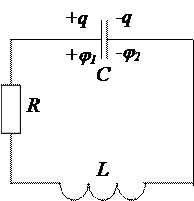Запишем для контура (рис.1.8.1) второй закон Кирхгофа:

Рис.1.8.1

 

IR+ j 1 - j 2 = e s или 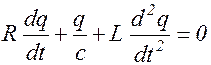. (1.8.1)

Разделим обе части уравнения (1.8.1) на L и введем обозначение:

b = 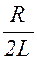. (1.8.2)

Учтя, что 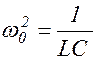, уравнение (1.8.1) перепишем в виде

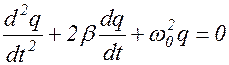. (1.8.3)

Уравнение (1.8.3) называется дифференциальным уравнением затухающих колебаний.

При выполнении условия b 2 < w 0 2 или 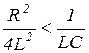, которое

называют условием малых затуханий, решение уравнения (1.8.3) имеет вид

q(t)=A0 e- b t cos( w t+ j 0 ), (1.8.4)

 

где 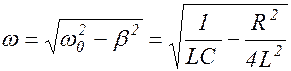- циклическая частота колебаний.

Амплитуда А затухающих колебаний равна

A(t)=A0 e- b t , (1.8.5)

 

где А0 - начальная амплитуда.

Если в начальный момент времени (t = 0), заряд на обкладках конденсатора равен q=q0 и ток в цепи отсутствует, то

 

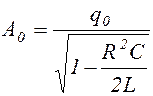. (1.8.6)

 

Скорость изменения амплитуды определяется величиной 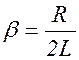, которую называют коэффициентом затухания.

 

График затухающих колебаний, соответствующий уравнению (1.8.4), изображен на рис.1.8.2

 


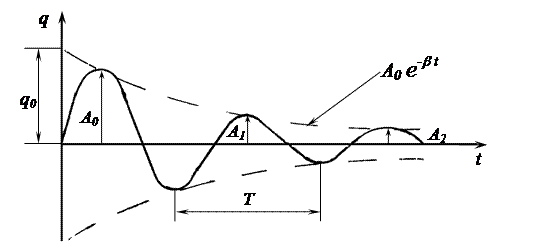Рис. 1.8.2

 

Напряжение на конденсаторе изменяется по закону:

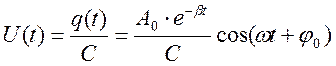. (1.8.7)

Изменение силы тока в колебательном контуре найдем, взяв производную по времени от выражения (1.8.4):

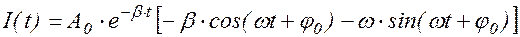. (1.8.8)

Промежуток времени t = t1 - t0, в течение которого амплитуда колебаний уменьшается в e раз, называется временем жизни колебаний. Выразим t через параметры контура.

По определению: 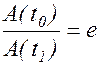. Из (1.8.5) следует:

 

 

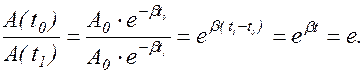
Откуда, получаем

b t = 1 или 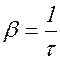. (1.8.9)

Таким образом, коэффициент затухания b обратен по величине времени жизни колебаний. С учетом (1.8.2) 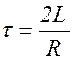. Отношение амплитуд через период колебания Т называется декрементом затухания:

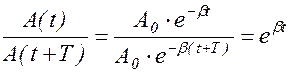. (1.8.10)

Натуральный логарифм отношения двух последующих амплитуд называется логарифмическим декрементом затухания l :

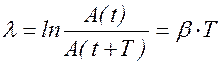. (1.8.11)

В течение времени жизни t система успевает совершить 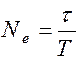колебаний. Подставляя в (1.8.11) значение b, определяемое формулой (1.8.9), получаем

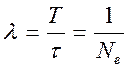. (1.8.12)