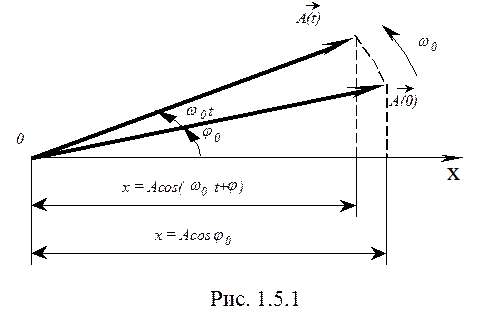§1.5. Представление гармонического колебания с помощью вектора-амплитуды

Дата: 2025-05-25; Просмотры: 3
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

 

Гармоническое колебание может быть представлено графически с помощью вращающегося вектора-амплитуды 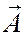. (рис. 1.5.1).

Вектор 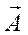, численно равный амплитуде колебания, равномерно вращается против часовой стрелки вокруг оси 0x, перпендикулярной плоскости чертежа, с угловой скоростью 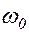. При этом его проекция на ось 0x изменяется по закону:

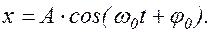(1.5.1)

Сравнение (1.5.1) с (1.2.8) показывает, что проекция этого вектора совершает гармонические колебания. Метод представления колебаний с помощью вектора-амплитуды в ряде случаев удобно применять для анализа сложного колебательного процесса.

§1.6. Сложение колебаний одинакового направления. Биения

 

а) Рассмотрим два колебания с одинаковыми частотами:

,

.

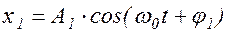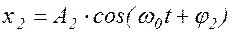Представим эти колебания с помощью вектора-амплитуды и сложим их графически (рис.1.6.1).

Из рисунка следует, что результирующее смещение (xрез=x1+x2) имеет вид

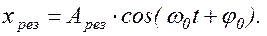(1.6.1)

 

 

Рис. 1.6.1

 

Таким образом, результирующее колебание будет гармоническим. Амплитуду результирующего колебания найдем по теореме косинусов:

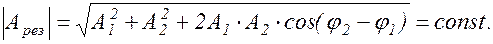(1.6.2)

Вектор 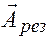вращается с той же угловой скоростью 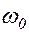. Амплитуда результирующего колебания зависит от разности фаз складываемых колебаний - ( 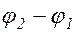). Если - 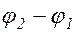=2k p, (k= 0,1,2), то Арез=А1+А2 (колебания в фазе).

Если 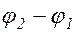=(2k+1)p, то 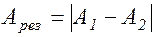, следовательно, колебания в противофазе.

Угол 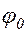, образованный вектором 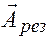с осью х в начальный момент времени, равен:

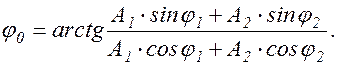(1.6.3)

б) Рассмотрим два колебания с разными круговыми частотами:

x1= 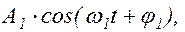x2= 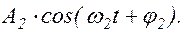(1.6.4)

Векторы 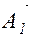и 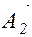вращаются с разными угловыми скоростями (w 1¹w2), разность фаз колебаний ( 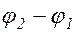) 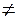const, поэтому меняется величина результирующей амплитуды: Арез 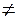const. Результирующее колебание не является гармоническим. Его можно представить в следующем виде:

x рез (t)=x1(t)+x2(t)=A(t) 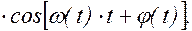(1.6.5)

Практический интерес представляет результат сложения колебаний с близкими частотами. В этом случае A(t) и j(t) медленно меняющиеся функции времени, а колебательный процесс называется биениями. В случае равных амплитуд A1=A2=A уравнения (1.6.4) можно сложить и получить уравнение биений:

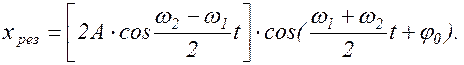(1.6.6)

Колебания вида (1.6.6) называются амплитудно-модулированными, причем амплитуда изменяется по закону:

A(t)= 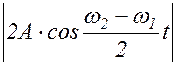. (1.6.7)

Величина A(t) периодически изменяется в пределах от 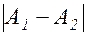до A1+A2 с частотой, называемой частотой биений:

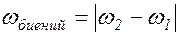. (1.6.8)

Частота результирующего колебания определяется формулой

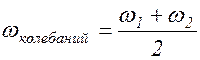. (1.6.9)

На рис.1.6.2 представлены биения, описываемые уравнением (1.6.6) при 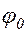= 0.

 


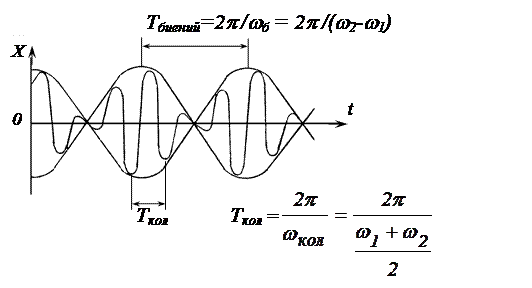Рис.1.6.2

§1.7. Сложение взаимно-перпендикулярных
колебаний

 

Рассмотрим два взаимно-перпендикулярных гармонических колебания, совершающихся вдоль осей 0x и 0y. Уравнения колебаний имеют вид:

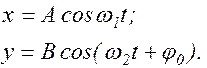(1.7.1)

I. Пусть частоты колебаний будут одинаковыми (w 1 = w 2 = w). В этом случае результирующее колебание будет определяться разностью фаз.

1) Если j 0 = 0, тогда из 1.7.1 получаем уравнение прямой линии

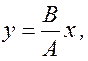(1.7.2)

то есть результирующее колебание является гармоническим колебанием, совершающимся вдоль прямой (1.7.2) с частотой w и амплитудой 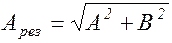(рис.1.7.1).

2) Если 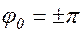, результирующее колебание является гармоническим колебанием, происходящим вдоль прямой, расположенной в II и IY квадрантах (рис.1.7.2).

3) Пусть 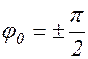. В этом случае траектория результирующего движения имеет вид

 

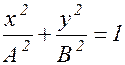. (1.7.3)

 

 

 


Если А = В - траекторией является окружность.

Если 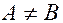- то эллипс.