Балтийский государственный технический университет
Министерство образования и науки РФ
БАЛТИЙСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
“ВОЕНМЕХ” им. Д.Ф. Устинова
Кафедра ракетостроение
Отчет по лабораторной работе №3
Компьютерное обеспечение технических решений
Выполнил: Сафиулин Р.Т.
Вариант № 9 Б3
Группа: КВ-61
Проверил: Степанов М.М.
Лабораторная работа №3
Динамика отделения головной части ракеты
с применением аэродинамических щитков
Тема: численное решение обыкновенных
дифференциальных уравнений
> restart;
with(plots):
Методические указания.
Цель и содержание работы:
Цель- ознакомление с численными методами решения обыкновенных дифференциальных уравнений на примере уравнения, описывающего процесс отделения головной части баллистической ракеты.
Содержание работы:
Рассматривается задача отделения головной части (ГЧ) баллистической ракеты с помощью аэродинамических щитков.
При этом сделаны следующие допущения:
- угол атаки равен нулю;
- тяга двигательной установки ракетного блока (РБ) равна нулю;
- массы головной части и ракетного блока постоянны в процессе разделения;
- зависимость коэффициента силы лобового сопротивления системы "ГЧ - РБ" от расстояния между ГЧ и РБ линейная;
- скорость раскрытия аэродинамических щитков постоянная.
В этом случае относительное движение ГЧ и РБ описывается следующей системой уравнений
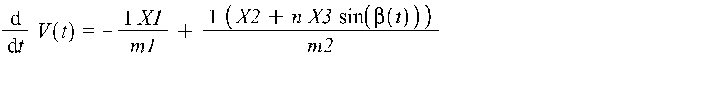
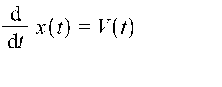
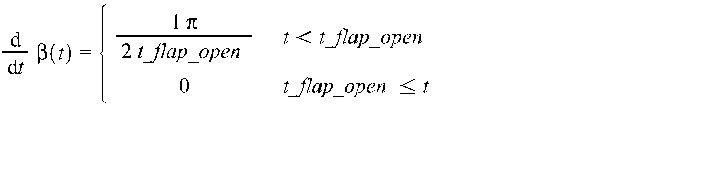
Здесь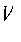 
- скорость ГЧ относительно РБ;
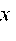- расстояние между ГЧ и РБ;
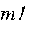- масса головной части;
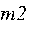- масса ракетного блока;
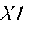- сила лобового сопротивления, действующая на головную часть;
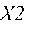- сила лобового сопротивления, действующая на ракетный блок;
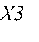- сила лобового сопротивления, действующая на каждый аэродинамический щиток;
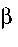- угол раскрытия щитка (от 0 до 
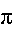/2);
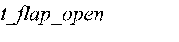- время раскрытия щитков;
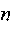- число щитков.
Порядок выполнения лабораторной работы:
- присвоить переменным V0, m1, m2, Cx1, Cx2и n значения в соответствии с полученным заданием;
- установить значение опции method команды dsolve, соответствующее методу в полученном задании. *)
- присвоить переменным a, b (размеры щитка) какие-либо начальные значения;
- произвести расчеты путем выбора пункта Edit \ Execute \ Worksheet главного меню среды Maple 13;
- путем подбора размеров щитка (значений a и b) обеспечить отделение ГЧ на заданное расстояние Lk к заданному моменту времени tk.
В данной работе используются классические численные методы решения обыкновенных дифференциальных уравнений. Поэтому для опции method команды dsolve следует использовать следующие значения:
- method=classical[foreuler]- прямой метод Эйлера;
- method=classical[heunform]- улучшенный метод Эйлера;
- method=classical[impoly]- модифицированный метод Эйлера;
- method=classical[rkn]- метод Рунге - Кутта n- го порядка (n = 2 .. 4).
Уравнения движения.
> equation_1 := diff(V(t),t) = -1/m1*X1 + 1/m2*(X2 + n*X3*sin(beta(t)));
equation_2 := diff(x(t),t) = V(t);
equation_3 := diff(beta(t),t) = piecewise(t < t_flap_open,Pi/(2*t_flap_open),
t >= t_flap_open,0);
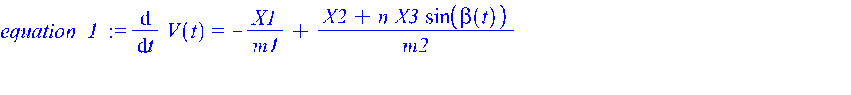
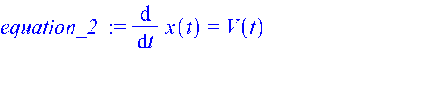
Дополнительные соотношения.
Аэродинамические силы
> X1 := cx1*Q*evalf(Sm);
X2 := cx2*Q*evalf(Sm);
X3 := cx3*Q*Sf;
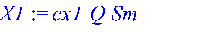
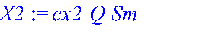
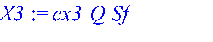
Площадь миделя ракетного блока
> Sm := Pi*d^2/4;
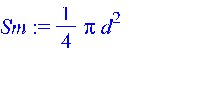
Площадь аэродинамического щитка
> Sf := a*b;
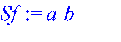
Коэффицент силы лобового сопротивления ракетного блока в зависимости от расстояния между блоком и головным отсеком
> cx2 := piecewise(x(t) < 3*d, cx2_0,
3*d <= x(t) and x(t) <= 4*d,
cx2_0 + (x(t) - 3*d)/(4*d - 3*d)
*(cx2_1 - cx2_0),
4*d <= x(t), cx2_1);
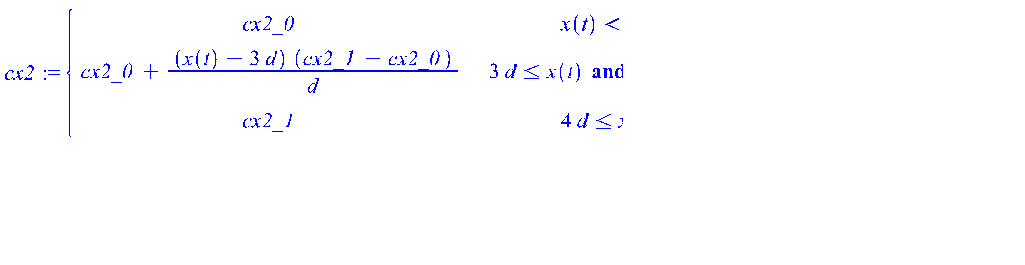
Скоростной напор
> Q := rho*V0^2/2;
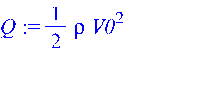
Плотность воздуха
> rho := rho0*(1-h/44300)^4.256;
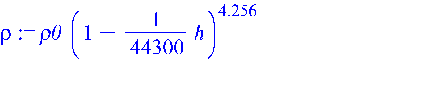
Исходные данные.
Высота, на которой производится отделение головного отсека, м
> h := 14400;
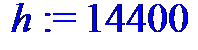
Скорость ракеты в конце активного участка, м/с
> V0 := 725.5;
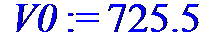
Размеры щитка, м
> a := 0.131;
b := 0.063;
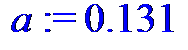
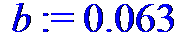
Число щитков
> n := 4;
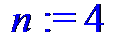
Диаметр миделя ракетного блока и основания головного отсека, м
> d := 0.480;
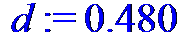
Коэффициенты силы лобового сопротивления ракетного блока и головного отсека
> cx1 := 0.52;
cx2_0 := 0.14;
cx2_1 := 0.94;
cx3 := 0.96;
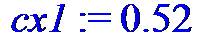
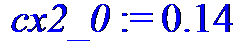
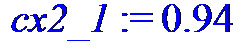
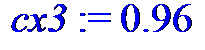
Массы головного отсека и ракетного блока, кг
> m1 := 562;
m2 := 174;
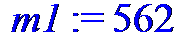
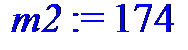
Время, за которое головной отсек должен отойти на заданное расстояние, сек
> tk := 1.2;
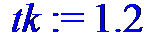
Время раскрытия щитков.
> t _ flap _ open := 0.6;
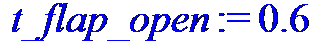
Плотность воздуха на уровне моря, кг/куб.м
> rho0 := 1.225;
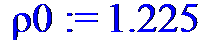
Расчет процесса отделения головного отсека.
Плотность и скоростной напор в момент отделения головного отсека
> rho;
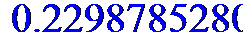
> Q;
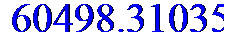
Начальные условия
> inicond := x (0)=0, V (0)=0, beta (0)=0;
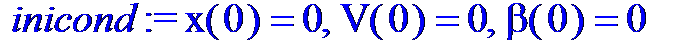
Интегрирование уравнений движения
> sol := dsolve({equation_1,equation_2,equation_3,inicond},
{x(t),V(t),beta(t)},
numeric,method=classical[impoly],
output=listprocedure);
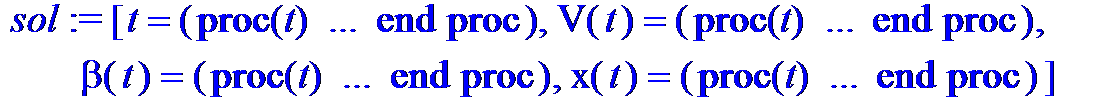
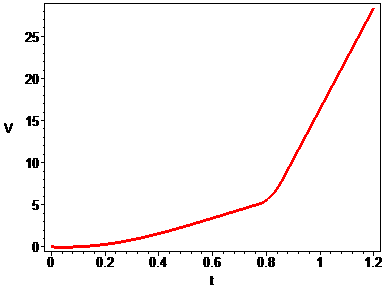
> odeplot(sol,[t,V(t)],0..tk,thickness=3,axes=boxed,labels=[t,V],style=line);
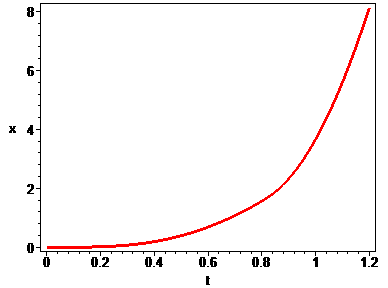
> odeplot(sol,[t,x(t)],0..tk,thickness=3,axes=boxed,labels=[t,x],style=line);
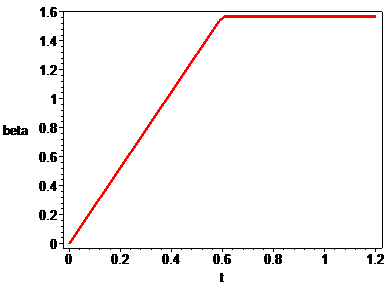
> odeplot(sol,[t,beta(t)],0..tk,thickness=3,axes=boxed,labels=[t,beta],style=line);
Расстояние между головным отсеком и ракетным блоком в заданный момент времени.
Именно это значение следует сравнивать с заданным расстоянием Lk.
> distance := subs(sol,x(t)):
distance(tk);
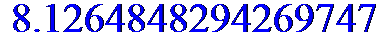
Lk = 8.2
Вывод: в данной лабораторной работе мы ознакомились с численными методами решения обыкновенных дифференциальных уравнений на примере уравнения, описывающего процесс отделения головной части баллистической ракеты.