Лабораторная работа №4
Министерство образования и науки РФ
БАЛТИЙСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
“ВОЕНМЕХ” им. Д.Ф. Устинова
Кафедра ракетостроение
Отчет по лабораторной работе №4
Компьютерное обеспечение технических решений
Выполнил: Сафиулин Р.Т.
Вариант № 9
Группа: КВ-61
Проверил: Степанов М.М.
Лабораторная работа №4
Определение размеров сферического баллона
Тема: численное решение систем алгебраических уравнений
> restart;
Цель- ознакомление с методом Ньютона -Рафсона для численного решения систем алгебраических уравнений
на примере задачи определения размеров сферического баллона.
Содержание работы:
В лабораторной работе рассматривается задача определения размеров сферического баллона высокого давления.
Такие баллоны используются в качестве аккумулятора давления в различных бортовых системах ракет.
Рабочее давление, объем баллона, а также свойства материала для изготовления баллона считаются заданными.
При этом необходимо обеспечить прочность баллона, а также учесть возможные ограничения на внешний диаметр баллона из условий размещения в отсеке ракеты.
В ходе проектирования требуется выбрать толщину стенки и внешний диаметр баллона.
Принятые обозначения:
- наружный диаметр баллона, 
;
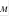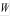- объем баллона, 
;
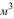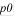- рабочее давление в баллоне, 
;
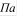- толщина стенки баллона, ;
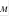- коэффициент безопасности;
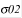- условный предел текучести материала баллона, Па.
Остальные обозначения вводятся по мере необходимости.
Порядок выполнения работы:
- присвоить переменным p0 и W значения в соответствии с полученным заданием;
- задать точность расчета для решения уравнения масс epsilon;
- произвести расчеты путем выбора пункта Edit \ Execute \ Worksheet главного меню среды Maple 13.
В ходе лабораторной работы требуется исследовать:
- условия сходимости метода Ньютона - Рафсона;
- зависимость числа итераций, требующихся для решения задачи, от значений начального приближения величин dи delta.
Выражения для поправок к переменным.
Система линейных алгебраических уравнений, используемая в методе Ньютона - Рафсона.
> eqn1 := dF_d * d_add + dF_delta * delta_add = - F;
> eqn2 := dG_d * d_add + dG_delta * delta_add = - G;
Здесь d_addи delta_add- поправки к переменным dи delta, определемые в процессе расчета.
> z := solve({eqn1,eqn2},{delta_add,d_add});
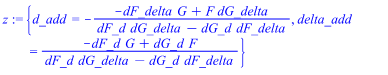
> delta_add := subs(z,delta_add);
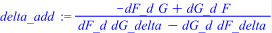
> d_add := subs(z,d_add);
Система уравнений.
Система уравнений для определения размеров баллона.
Условие прочности:
> F := f*p0*(d/2-delta)/(2*delta) - sigma02;
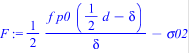
Заданный объем баллона:
> G := 4/3*Pi*(d/2-delta)^3 - W;
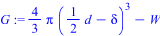
Частные производные:
> dF_d := diff(F,d);
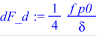
> dF_delta := diff(F,delta);
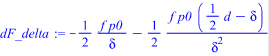
> dG_d := diff(G,d);
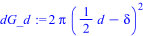
> dG_delta := diff(G,delta);
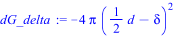
Исходные данные.
> f := 1.5;
p 0 := 90;
W := 0.9;
sigma02 := 12e8;
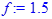
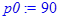
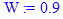
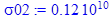
Определение размеров баллона.
Начальное приближение.
> d := 0.5;
delta := 0.01;
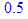
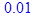
Точность расчетов:
> epsilon := 0.001;
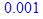
Максимальное число итераций:
> i _ max := 100;
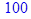
Решение системы нелинейных уравнений методом Ньютона-Рафсона:
> for i from 1 while ((abs(F) > epsilon
or abs(evalf(G)) > epsilon)
and i <= i_max) do
delta := delta + evalf(delta_add):
d := d + evalf(d_add):
print(i,"d=",d,"delta=",delta,
"F=",abs(F),"G=",abs(evalf(G))):
end do:
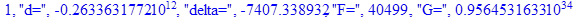
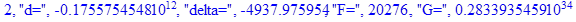
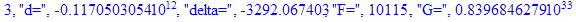
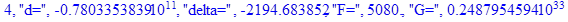
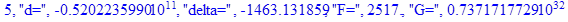
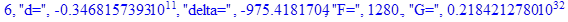
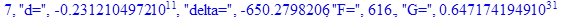
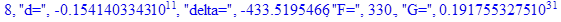
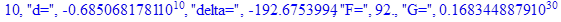
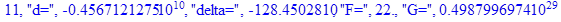
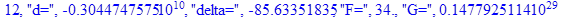
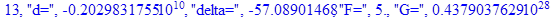
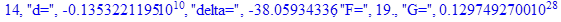
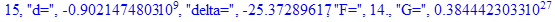
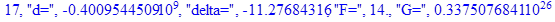
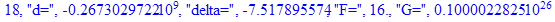
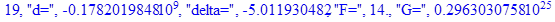
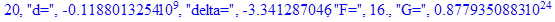
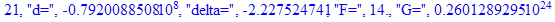
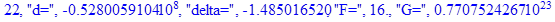
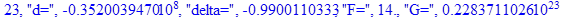
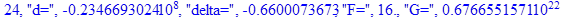
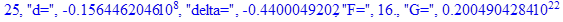
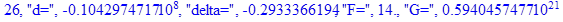
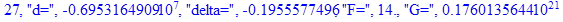
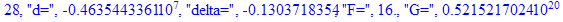
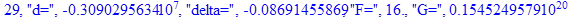
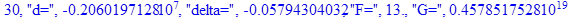
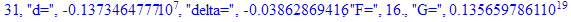
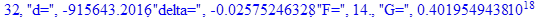
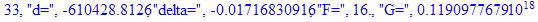
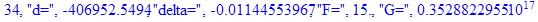
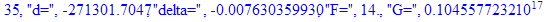
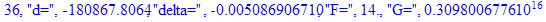
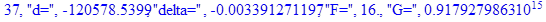
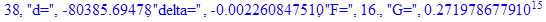
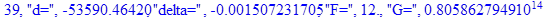
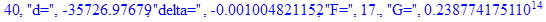
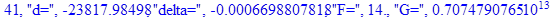
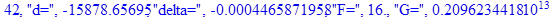
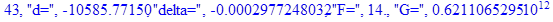
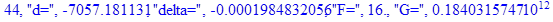
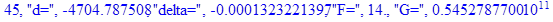
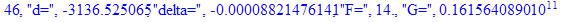
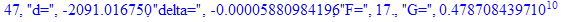
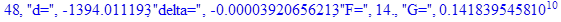
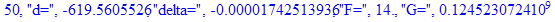
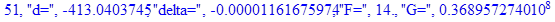
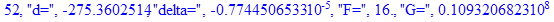
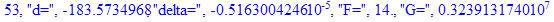
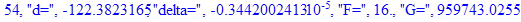
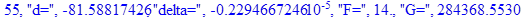
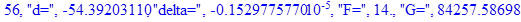
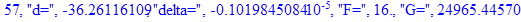
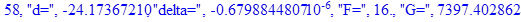
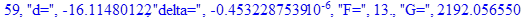
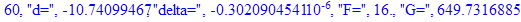
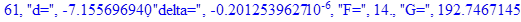
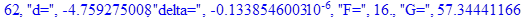
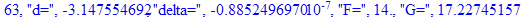
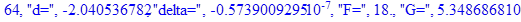
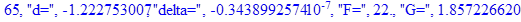
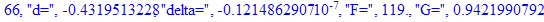
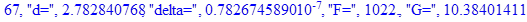
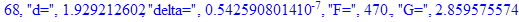
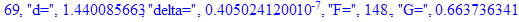
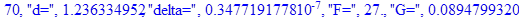
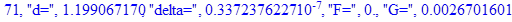
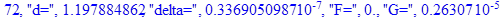
Вывод: в ходе 4 лабораторной работе мы ознакомились с методом Ньютона – Рафсона для численного решения систем алгебраических уравнений на примере задачи определения размеров сферического баллона, а также убедились в том, что программный пакет Maple наилучшим образом подходит для решения разнообразных прикладных задач данным методом.