4 Определение основных характеристик диагностических параметров (часть 1)
Содержание
1) Введение……………………………………………………………2
2) Исходные данные………………………………………………….3
3) Определение основных характеристик диагностических параметров (часть 1)…………………………………………………………….4
4) Определение основных характеристик диагностических параметров (часть 2)…………………………………………………………….7
5) Заключение………………………………………………………...11
6) Список литературы………………………………………………..12
1. ВВЕДЕНИЕ
Надёжность — свойство объекта сохранять во времени в установленных пределах значения всех параметров, характеризующих способность выполнять требуемые функции в заданных режимах и условиях применения, технического обслуживания, хранения и транспортирования.
Интуитивно надёжность объектов связывают с недопустимостью отказов в работе. Это есть понимание надёжности в «узком» смысле — свойство объекта сохранять работоспособное состояние в течение некоторого времени или некоторой наработки. Иначе говоря, надёжность объекта заключается в отсутствии непредвиденных недопустимых изменений его качества в процессе эксплуатации и хранения. Надёжность тесно связана с различными сторонами процесса эксплуатации. Надёжность в «широком» смысле — комплексное свойство, которое в зависимости от назначения объекта и условий его эксплуатации может включать в себя свойства безотказности, долговечности, ремонтопригодности и сохраняемости, а также определённое сочетание этих свойств.
Для количественной оценки надёжности используют так называемые единичные показатели надёжности (характеризуют только одно свойство надёжности) и комплексные показатели надёжности (характеризуют несколько свойств надёжности).
Надежность в инженерной практике отличается от безопасности отношением к видам опасностей, с которыми она имеет дело. Надежность в технике главным образом связана с определением стоимостных показателей. Они относятся к тем опасностям в смысле надежности, которые могут перерасти в аварии с частичной потерей доходов для компании или заказчика. Это может произойти из-за потери по причине неготовности системы, неожиданно высоких затрат на запасные части и ремонт, перерывов в нормальной работе и т.п. Безопасность относится к тем случаям проявления опасности, которые могут привести к потенциально тяжелым авариям. Требования по безопасности функционально связаны с требованиями по надежности, но характеризуются более высокой ответственностью. Безопасность имеет дело с нежелательными опасными событиями для жизни людей и окружающей среды в том же смысле, что и надежность, но не связана напрямую со стоимостными показателями и не относится к действиям по восстановлению после отказов и аварий. У безопасности другой уровень важности отказов в обществе и контроля со стороны государства. Безопасность часто контролируется государством (например, атомная промышленность, космос, оборона, железные дороги и нефтегазовый сектор).
2. ИСХОДНЫЕ ДАННЫЕ
| a1=0,2 | b1=42,03 | c1=0,121 |
| a2=5,406 | b2=-20,65 | c2=-0,485 |
| a3=0,844 | b3=11,71 | c3=-423,977 |
| a4=0,878 | b4=28,278 | c4-94,569 |
| a5=2,083 | b5=-23,156 | c5=0,377 |
3. ОПРЕДЕЛЕНИЕ ОСНОВНЫХ ХАРАКТЕРИСТИК ДИАГНОСТИЧЕСКИХ ПАРАМЕТРОВ (часть 1)
Зависимость диагностического параметра ДП от структурного параметра СП можно выразить следующей зависимостью:
ДП i = Fi (СП)= ai + biC П+ ciC П2,
где ai , bi , ci – постоянные коэффициенты.
Далее, по полученным у преподавателя значениям коэффициентов для пяти диагностических параметров a1– a5, b1– b5, c1– c5, нужно построить зависимость диагностических параметров от структурного параметра (рис. 1).

Рис. 1 Зависимость диагностических параметров от структурного параметра
Начальное значение структурного параметра СПн=0,01, предельное значение структурного параметра СПп=0,075.
СП1=0,01; СП2=0,025; СП3=0,04; СП4=0,055; СП5=0,075.
ДП11= Fi (СП)= ai + biC П+ ciC П2=0,2+42,03∙0,01+0,121∙0,012=0,62
ДП12= Fi (СП)= ai + biC П+ ciC П2=0,2+42,03∙0,025+0,121∙0,0252=1,25
ДП13= Fi (СП)= ai + biC П+ ciC П2=0,2+42,03 ∙0,04+0,121∙0,042=1,88
ДП14= Fi (СП)= ai + biC П+ ciC П2=0,2+42,03∙0,055+0,121∙0,0552=2,51
ДП15= Fi (СП)= ai + biC П+ ciC П2=0,2+42,03∙0,075+0,121∙0,0752=3,35
ДП21= Fi (СП)= ai + biC П+ ciC П2=5,406-20,65∙0,01-0,485∙0,012=5,2
ДП22= Fi (СП)= ai + biC П+ ciC П2=5,406-20,65∙0,025-0,485∙0,0252=4,89
ДП23= Fi (СП)= ai + biC П+ ciC П2=5,406-20,65∙0,04-0,485∙0,042=4,58
ДП24= Fi (СП)= ai + biC П+ ciC П2=5,406-20,65∙0,055-0,485∙0,0552=4,27
ДП25= Fi (СП)= ai + biC П+ ciC П2=5,406-20,65∙0,075-0,485∙0,0752=3,85
ДП31= Fi (СП)= ai + biC П+ ciC П2=0,844+11,71∙0,01-423,977∙0,012=0,92
ДП32= Fi (СП)= ai + biC П+ ciC П2=0,844+11,71∙0,025-423,977∙0,0252=0,87
ДП33= Fi (СП)= ai + biC П+ ciC П2=0,844+11,71∙0,04-423,977∙0,042=0,63
ДП34= Fi (СП)= ai + biC П+ ciC П2=0,844+11,71∙0,055-423,977∙0,0552=0,21
ДП35= Fi (СП)= ai + biC П+ ciC П2=0,844+11,71∙0,075-423,977∙0,0752=-0,66
ДП41= Fi (СП)= ai + biC П+ ciC П2=0,878+28,278∙0,01-94,569∙0,012=1,15
ДП42= Fi (СП)= ai + biC П+ ciC П2=0,878+28,278∙0,025-94,569∙0,0252=1,52
ДП43= Fi (СП)= ai + biC П+ ciC П2=0,878+28,278∙0,04-94,569∙0,042=1,86
ДП44= Fi (СП)= ai + biC П+ ciC П2=0,878+28,278∙0,055-94,569∙0,0552=2,15
ДП45= Fi (СП)= ai + biC П+ ciC П2=0,878+28,278∙0,075-94,569∙0,0752=2,46
ДП51= Fi (СП)= ai + biC П+ ciC П2=2,083-23,156∙0,01+0,377∙0,012=1,85
ДП52= Fi (СП)= ai + biC П+ ciC П2=2,083-23,156∙0,025+0,377∙0,0252=1,5
ДП53= Fi (СП)= ai + biC П+ ciC П2=2,083-23,156∙0,04+0,377∙0,042=1,16
ДП54= Fi (СП)= ai + biC П+ ciC П2=2,083-23,156∙0,055+0,377∙0,0552=0,81
ДП55= Fi (СП)= ai + biC П+ ciC П2=2,083-23,156∙0,075+0,377∙0,0752=0,35
3.1 Определение однозначности диагностических параметров
Диагностический параметр будет однозначным, если первая производная функции диагностического параметра от структурного параметра в диапазоне изменения структурного параметра от начального СПн до предельного СПп не равна нулю. Для этого приравняем производную функции диагностического параметра от структурного параметра к нулю и выразим из этого равенства значение структурного параметра C П ext соответствующее экстремуму функции:
ДП i ′= Fi ′(СП)= bi +2ciC П ext = 0; C П extr = – bi /2ci ;
- далее необходимо вычислить значения C П extr для каждого из пяти диагностических параметров;
- определить, попадает ли C П extr в диапазон от начального СПн до предельного СПп значений диагностического параметра, сделать вывод об однозначности диагностических параметров, а результаты занести в табл. 1.
Таблица 1
| Результаты и выводы | Диагностические параметры | ||||
| 1 | 2 | 3 | 4 | 5 | |
| Рассчитанное значение C П extr | -173,67 | -2,76 | 0,005 | 5,59 | 9,95 |
| Факт попадания C П extr в диапазон СПн - СПп (да или нет) | нет | нет | да | Нет | Нет |
| Вывод об однозначности диагностического параметра (да или нет) | нет | нет | нет | Нет | Нет |
Вывод: все пять диагностических параметров является неоднозначными, так как первая производная функции диагностического параметра от структурного параметра в диапазоне изменения структурного параметра от начального СПн до предельного СПп не равна нулю.
3.2 Определение чувствительности диагностических параметров
Далее необходимо определить чувствительность диагностических параметров для начального СПн , промежуточного СПпр и предельного СПп значений структурного параметра по формуле
К = | F ′(СП)| = | bi +2ciC П|
Результаты представлены в табл. 2.
Таблица 2
| Значение структурного параметра | Чувствительность диагностических параметров (К) | ||||
| 1 | 2 | 3 | 4 | 5 | |
| СПн | 42,033 | 20,66 | 20,19 | 30,17 | 23,16 |
| СПпр | 42,04 | 20,69 | 45,63 | 35,84 | 23,19 |
| СПп | 42,05 | 20,72 | 75,31 | 42,46 | 23,21 |
Дальше провести анализ чувствительности диагностических параметров для трех значений структурного параметра: СПн, СПпр, СПп. Результаты анализа приведены в табл. 3. Результатом анализа является место (1-е, 2-е, 3-е и так далее), занимаемое диагностическим параметром относительно других диагностических параметров по критерию чувствительности;
Таблица 3
| Значение СП | Место ДП по чувствительности для соответствующего значения СП | ||||
| 1 | 2 | 3 | 4 | 5 | |
| СПн | 1 | 4 | 5 | 2 | 3 |
| СПпр | 1 | 4 | 5 | 2 | 3 |
| СПп | 1 | 4 | 2 | 5 | 3 |
Вывод: самый чувствительный диагностический параметр к изменению структурного параметра это первый диагностический параметр.
4 ОПРЕДЕЛЕНИЕ ОСНОВНЫХ ХАРАКТЕРИСТИК ДИАГНОСТИЧЕСКИХ ПАРАМЕТРОВ (часть 1)
4.1 Оценка стабильности диагностических параметров
Стабильность диагностического параметра определяется разбросом его значений при многократном измерении на объектах, имеющих одну и ту же величину соответствующего структурного параметра (рис. 2). Его оценивают с помощью среднеквадратичного отклонения и коэффициента вариации.

Зависимость среднеквадратического отклонения от диагностического параметра выражается следующей зависимостью:
σi = Fi (ДП i )=|(0,4 ДП i -0,01 ДП i 2 )/(1,5-0,5/ i )|, где i – порядковый номер диагностического параметра.
Далее определяем среднеквадратичное отклонение σ и коэффициент вариации ν диагностических параметров для начального СПн, промежуточного СПпр и предельного СПп значений структурного параметра. Результаты расчетов представлены в таблице 4.
σ н1 = Fi (ДП i )=|(0,4 ДП i -0,01 ДП i 2 )/(1,5-0,5/ i )|= (0,4×0,62-0,01×0,622)/1=0,24
σ н2 = Fi (ДП i )=|(0,4 ДП i -0,01 ДП i 2 )/(1,5-0,5/ i )|= (0,4×1,25-0,01×1,252)/1,25=0,48
σ н3 = Fi (ДП i )=|(0,4 ДП i -0,01 ДП i 2 )/(1,5-0,5/ i )|= (0,4×1,88-0,01×1,882)/1,34=0,72
σ н4 = Fi (ДП i )=|(0,4 ДП i -0,01 ДП i 2 )/(1,5-0,5/ i )|= (0,4×2,51-0,01×2,51 2)/1,375=0,94
σ н5 = Fi (ДП i )=|(0,4 ДП i -0,01 ДП i 2 )/(1,5-0,5/ i )|= (0,4×3,35-0,01×3,352)/1,4=1,23
σ пр1 = Fi (ДП i )=|(0,4 ДП i -0,01 ДП i 2 )/(1,5-0,5/ i )|= (0,4×0,92-0,01×0,922)/1=0,27
σ пр2 = Fi (ДП i )=|(0,4 ДП i -0,01 ДП i 2 )/(1,5-0,5/ i )|= (0,4×0,87-0,01×0,872)/1,25=0,26
σ пр3 = Fi (ДП i )=|(0,4 ДП i -0,01 ДП i 2 )/(1,5-0,5/ i )|= (0,4×0,63-0,01×0,632)/1,34=0,186
σ пр4 = Fi (ДП i )=|(0,4 ДП i -0,01 ДП i 2 )/(1,5-0,5/ i )|= (0,4×0,21-0,01×0,21 2)/1,375=0,063
σ пр5 = Fi (ДП i )=|(0,4 ДП i -0,01 ДП i 2 )/(1,5-0,5/ i )|= (0,4×(-0,66)-0,01×(-0,66)2)/1,4=0,194
σ п1 = Fi (ДП i )=|(0,4 ДП i -0,01 ДП i 2 )/(1,5-0,5/ i )|= (0,4×1,85-0,01×1,85 2)/1=0,50
σ п2 = Fi (ДП i )=|(0,4 ДП i -0,01 ДП i 2 )/(1,5-0,5/ i )|= (0,4×1,5-0,01×1,52)/1,25=0,41
σ п3 = Fi (ДП i )=|(0,4 ДП i -0,01 ДП i 2 )/(1,5-0,5/ i )|= (0,4×1,16-0,01×1,16 2)/1,34=0,32
σ п4 = Fi (ДП i )=|(0,4 ДП i -0,01 ДП i 2 )/(1,5-0,5/ i )|= (0,4×0,81-0,01×0,81 2)/1,375=0,23
σ п5 = Fi (ДП i )=|(0,4 ДП i -0,01 ДП i 2 )/(1,5-0,5/ i )|= (0,4×0,35-0,01×0,352)/1,4=0,1
Таблица 4
| Значение структурного параметра | σ/ν | ||||
| 1 | 2 | 3 | 4 | 5 | |
| СПн | 0,24 | 0,48 | 0,72 | 0,94 | 1,23 |
| СПпр | 0,27 | 1,26 | 0,186 | 0,063 | 0,194 |
| СПп | 50 | 0,41 | 0,32 | 0,23 | 0,1 |
Определяем коэффициент вариации ν.
nн=σ ̅ x / ̅ x=2,81/15= 0,24
nпр=σ ̅ x / ̅ x=3,151/15= 0,065
nп=σ ̅ x / ̅ x=3,128/15= 0,104
Далее проведем анализ стабильности диагностических параметров для трех значений структурного параметра: СПн, СПпр, СПп. Результаты анализа занесены в таблицу 5. Результатом анализа является место (1-е, 2-е, 3-е и так далее), занимаемое диагностическим параметром0 относительно других диагностических параметров по критерию стабильности.
Таблица 5
| Значение структурного параметра | Место диагностического параметра по стабильности | ||||
| 1 | 2 | 3 | 4 | 5 | |
| Сн | 5 | 1 | 4 | 3 | 2 |
| Спр | 2 | 1 | 5 | 4 | 3 |
| Сп | 1 | 2 | 5 | 3 | 4 |
Вывод: самым стабильным из трех значений структурного параметра является второй диагностический параметр.
4.2 Определение информативности диагностических параметров
Информативность диагностического параметра характеризует достоверность диагноза, получаемого в результате измерения значений параметра. Информативность определяют из совместного анализа плотностей распределения f (ДПи) и f (ДПн) значений параметра, соответствующих заведомо исправным и неисправным объектам. Ошибка диагноза будет тем меньше, чем сильнее отличаются средние значения параметра для исправного и для неисправного состояний объекта и чем меньше разброс значений параметра для каждого состояния. Поэтому для оценки информативности используем следующею величину:
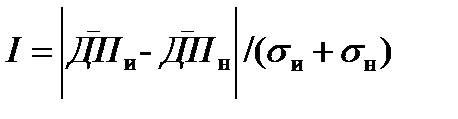
где 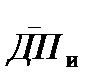 – среднее значение диагностических параметров для исправных объектов;
– среднее значение диагностических параметров для исправных объектов; 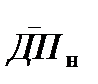 – среднее значение диагностических параметров для неисправных объектов; sи – среднеквадратическое отклонение значений диагностических параметров для исправных объектов; sн – среднеквадратическое отклонение значений диагностических параметров для неисправных объектов.
– среднее значение диагностических параметров для неисправных объектов; sи – среднеквадратическое отклонение значений диагностических параметров для исправных объектов; sн – среднеквадратическое отклонение значений диагностических параметров для неисправных объектов.
Информативность диагностического параметра определится при условии, что исправным объект считается при номинальном значении диагностического параметра, а неисправным – при предельном значении диагностического параметра. Определяем информативность всех пяти диагностических параметров и проранжироваем их.
I1=|1,966-2,07|/(0,252+1,278)=0,068
I2=|1,966-2,07|/(1,496+1,184)=0,038
I3=|1,966-2,07|/(0,276-0,0122)=0,394
I4=|1,966-2,07|/(0,341+0,74)=0,096
I5=|1,966-2,07|/(0,4494+0,023)=0,22
Вывод: самым информативным является третий диагностических параметр.
5 ЗАКЛЮЧЕНИЕ
В ходе выполнения курсовой работы мы вычислили основные характеристики диагностических параметров от структурного параметра и выяснили что с увеличением эксплуатации и нагрузки на автомобиль возрастает количество отказов. Так для начального структурного параметра (СПн) как и для промежуточного (СПпр) наиболее подходящий диагностический параметр является первый. Для предельного структурного параметра (СПп) будет являться третий.
Список литературы
1. Проников А.С. “Надежность машин” М.: Машиностроение, 1978. - 592 с.
2. Диагностические параметры [Электронный ресурс] – Режим доступа http://mydocx.ru/3-39280.html (Дата обращения 06.11.2015)
3. Википедия. Надежность [Электронный ресурс] – Режим доступа https://ru.wikipedia.org/wiki/%D0%9D%D0%B0%D0%B4%D1%91%D0%B6%D0%BD%D0%BE%D1%81%D1%82%D1%8C (Дата обращения 03.11.2015)








