Скалярное произведение векторов
Скалярным произведением двух ненулевых векторов 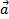 и
и 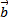 называется число, равное произведению длин этих векторов на косинус угла между ними:
называется число, равное произведению длин этих векторов на косинус угла между ними: 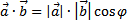 , где
, где 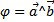 .
.
Так как 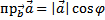 , а
, а 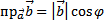 , то
, то 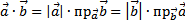 , то есть скалярное произведение двух векторов равно модулю одного из них, умноженному на проекцию другого на ось, сонаправленную с первым вектором.
, то есть скалярное произведение двух векторов равно модулю одного из них, умноженному на проекцию другого на ось, сонаправленную с первым вектором.
Свойства скалярного произведения
1. Скалярное произведение коммутативно, т.е. 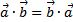 .
.
2. Скалярное произведение обладает сочетательным свойством 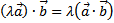 .
.
3. Скалярное произведение обладает распределительным свойством 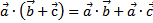 .
.
4. Скалярный квадрат вектора равен квадрату его длины 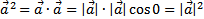 . В частности,
. В частности, 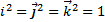 .
.
5. Если два ненулевых вектора 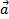 и
и 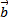 взаимно перпендикулярны, то их скалярное произведение равно нулю (
взаимно перпендикулярны, то их скалярное произведение равно нулю ( 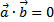 ) и, наоборот, если
) и, наоборот, если 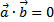 , то векторы
, то векторы 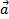 и
и 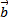 взаимно перпендикулярны. В частности,
взаимно перпендикулярны. В частности, 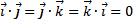 .
.
Пусть даны два вектора 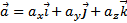 и
и 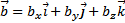 , тогда скалярное произведение двух векторов равно сумме произведений их соответственных координат
, тогда скалярное произведение двух векторов равно сумме произведений их соответственных координат
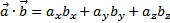 .
.
Из определения скалярного произведения следует, что
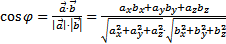 ,
,
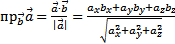 ,
,
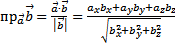 .
.
Рассмотрим материальную точку, которая перемещается прямолинейно из положения А в положение В под действием постоянной силы 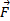 , образующей угол φ с направлением перемещения
, образующей угол φ с направлением перемещения 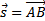 . Работа постоянной силы при прямолинейном перемещении её точки приложения равна скалярному произведению вектора силы на вектор перемещения
. Работа постоянной силы при прямолинейном перемещении её точки приложения равна скалярному произведению вектора силы на вектор перемещения 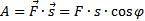 .
.
Векторное произведение
Три некомпланарных вектора 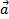 ,
, 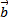 и
и 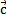 , взятые в указанном порядке, образуют правую тройку, если с конца третьего вектора
, взятые в указанном порядке, образуют правую тройку, если с конца третьего вектора 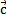 кратчайший поворот от первого вектора
кратчайший поворот от первого вектора 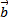 ко второму вектору
ко второму вектору 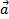 виден против часовой стрелки, и левую, если по часовой (рис. 1)
виден против часовой стрелки, и левую, если по часовой (рис. 1)
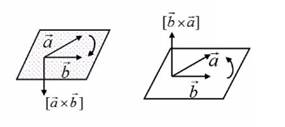
Рис. 1.
Векторным произведением вектора 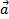 на вектор
на вектор 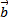 называется вектор
называется вектор 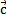 , который перпендикулярен векторам
, который перпендикулярен векторам 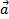 и
и 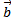 и имеет длину, численно равную площади параллелограмма, построенного на векторах
и имеет длину, численно равную площади параллелограмма, построенного на векторах 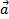 и
и 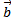 , т.е.
, т.е. 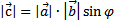 , где
, где 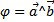 . Векторы
. Векторы 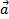 ,
, 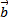 и
и 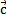 образуют правую тройку. Векторное произведение обозначается
образуют правую тройку. Векторное произведение обозначается 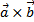 или
или 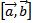 .
.
Из определения векторного произведения вытекают следующие соотношения между ортами 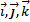 :
: 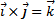 ,
, 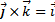 ,
, 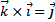 .
.
Свойства векторного произведения
1. При перестановке множителей векторное произведение меняет знак на противоположный, т.е. 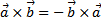 .
.
2. Векторное произведение обладает сочетательным свойством: 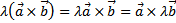 .
.
3. Два ненулевых вектора 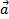 и
и 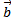 коллинеарны тогда и только тогда, когда
коллинеарны тогда и только тогда, когда 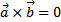 . В частности,
. В частности, 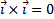 ,
, 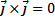 ,
, 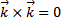 .
.
4. Векторное произведение обладает распределительным свойством
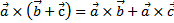 .
.
Пусть даны два вектора 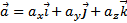 и
и 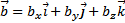 , тогда векторное произведение двух векторов равно определителю, первую строку которого образуют орты
, тогда векторное произведение двух векторов равно определителю, первую строку которого образуют орты 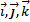 :
:
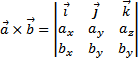 .
.
Из определения векторного произведения 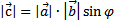 следует, что площадь параллелограмма
следует, что площадь параллелограмма 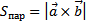 равна модулю векторного произведения векторов
равна модулю векторного произведения векторов 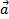 и
и 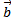 , на которых он построен. Соответственно площадь треугольника равна
, на которых он построен. Соответственно площадь треугольника равна 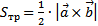 .
.
Пусть в точке А приложена сила 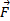 , тогда момент силы
, тогда момент силы 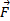 относительно точки О представляет собой вектор
относительно точки О представляет собой вектор 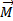 , численно равный произведению силы на плечо
, численно равный произведению силы на плечо 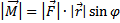 .
.
Смешанное произведение
Рассмотрим произведение трёх векторов 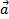 ,
, 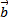 и
и 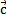 , составленное следующим образом
, составленное следующим образом
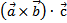 – здесь первые два вектора перемножаются векторно, а их результат скалярно. Такое произведение называется векторно-скалярным, или смешанным, произведением трёх векторов. Смешанное произведение представляет собой число.
– здесь первые два вектора перемножаются векторно, а их результат скалярно. Такое произведение называется векторно-скалярным, или смешанным, произведением трёх векторов. Смешанное произведение представляет собой число.
Свойства смешанного произведения
1. Смешанное произведение не меняется при циклической перестановке его множителей, т.е. 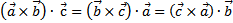 .
.
2. Смешанное произведение не меняется не меняется при перемене местами знаков скалярного и векторного произведения 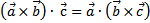 .
.
3. Смешанное произведение меняет знак при перемене местами любых двух векторов.
4. Смешанное произведение трёх ненулевых векторов 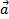 ,
, 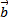 и
и 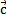 равно нулю тогда и только тогда, кода они компланарны и, наоборот, если векторы компланарны, то их смешанное произведение равно нулю.
равно нулю тогда и только тогда, кода они компланарны и, наоборот, если векторы компланарны, то их смешанное произведение равно нулю.
Пусть даны три вектора 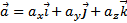 ,
, 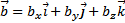 и
и 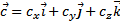 тогда векторное произведение трёх векторов равно определителю, составленному из их координат
тогда векторное произведение трёх векторов равно определителю, составленному из их координат
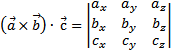 .
.
Смешанное произведение равно объёму параллелепипеда 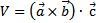 , построенного на этих векторах, взятому со знаком «плюс», если векторы образуют правую тройку, и со знаком «минус», если они образуют левую тройку. Из геометрического смысла следует, что объём пирамиды равен
, построенного на этих векторах, взятому со знаком «плюс», если векторы образуют правую тройку, и со знаком «минус», если они образуют левую тройку. Из геометрического смысла следует, что объём пирамиды равен 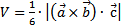 .
.
Пример. Даны вершины пирамида А (1, 2, 3), В (0, -1, 1), С (2, 5, 2) и D (3, 0, -2). Найти объём пирамиды.
Решение. Найдём координаты векторов, исходящих из одной вершины.
Например, 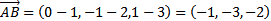 ;
; 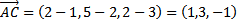 ;
; 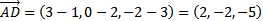 . Тогда объём пирамиды равен
. Тогда объём пирамиды равен
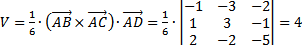 .
.








