Максимально допустимая высота всасывания

Дата: 2025-06-14; Просмотры: 1

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Выбрав допустимый кавитационный запас, можно найти для данного насоса максимально допустимую высоту всасывания.

Из уравнения (3) высота всасывания

Из уравнения (4)

Подставив (8) в (7), получим

Максимальная геометрическая высота всасывания насосов не может быть более 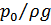. При атмосферном давлении 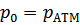максимальная геометрическая высота всасывания воды насосами не может быть более 10 м. Высота всасывания центробежных насосов обычно не превышает б...7 м. Если по расчету получается 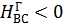, то насос необходимо ставить ниже уровня жидкости в приемном резервуаре.

При эксплуатации насоса следует контролировать, не работает ли насос в режиме развитой кавитации. Такой контроль удобно производить по показаниям вакууметра, установленного на всасывающем патрубке. Для этого надо знать допустимый вакуум на входе в насос. Для характеристики всасывающей способности насоса вводится параметр вакуумметрическая высота всасывания

Из уравнения (4)

Подставив (11) в (10), получим

Слайд

В стандарте ГОСТ 6134-2007 используется термин “надкавитационный напор на входе NPSH (кавитационный запас)”.

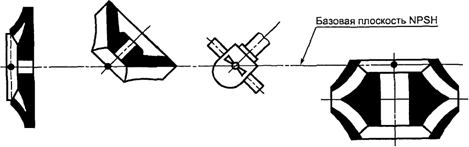
Рисунок 6. Базовая плоскость NPSH

NPSH – это базовая плоскость:

- для многоступенчатых насосов – горизонтальная плоскость, проходящая через центр окружности, которую описывают наиболее удаленные точки входных кромок лопаток рабочего колеса первой ступени.

- для насосов двухстороннего входа, с вертикальной или наклоненной осью вращения – плоскость, проходящая через наиболее высокий центр окружности.

Производитель (изготовитель) может определить положение этой плоскости более точно по отношению к характерным точкам насоса в соответствии с рисунком 6.

Слайд 6

Критическое число кавитации

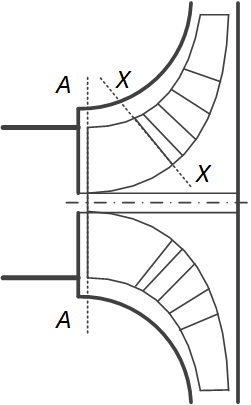
Рис. Схема движения частицы жидкости во всасывающей линии

Кавитация возникает в области пониженного давления, расположенной на тыльной стороне лопатки вблизи входной кромки. Напишем уравнение Бернулли для относительного движения жидкости для сечения струйки, расположенного перед входом на лопатки рабочего колеса A - A, и сечения X- X, в котором давление минимально. Так как эти сечения близки одно к другому, то 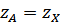и 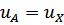. Гидравлическими потерями пренебрегаем. При этом

откуда

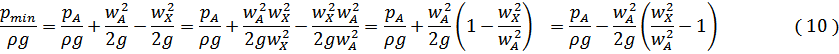
Кавитация начинается при равенстве минимального давления давлению насыщенного пара перекачиваемой жидкости, т.е. при 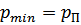. При этом

есть критическое число кавитации.

Для кинематически подобных потоков отношение скоростей 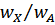, и, следовательно, критическое число кавитации 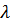– одинаковы. Критическое число кавитации зависит от формы проточной части входных элементов рабочего колеса и направления потока на входе в него (режима работы насоса).

Слайд 7

Напишем уравнение Бернулли для сечений струйки жидкости, расположенной на входе в подвод и непосредственно перед входом на лопатку рабочего колеса. При этом примем, что гидравлические потери в подводе малы и ими можно пренебречь

Из уравнений (9) и (10) получим

Для кавитационных режимов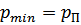

Или, согласно уравнению (5)

Полученное уравнение является основным расчетным уравнением кавитации. Из выражения (13) следует, что давление 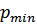тем меньше, чем больше скорости 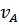и . И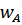з выражения (15) следует, что критический кавитационный запас зависит только от скорости движения жидкости, определяемой конструкцией насоса и режимом его работы. Он не зависит от барометрического давления и мало зависит от рода и температуры жидкости.

Слайд 8

Кавитационный коэффициент быстроходности

При кинематическом подобии насосов скорость жидкости у входа в насос пропорциональна окружной скорости рабочего колеса

где n – скорость вращения рабочего колеса;

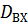– диаметр рабочего колеса;

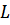– характерный линейный размер насоса.

Подача насоса Q равна произведению скорости потока 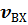на площадь сечения у входа в насос

Для двух насосов, отмечаемых индексами 1 и 2

Теперь выведем формулу пересчета критического кавитационного запаса для двух геометрически подобных насосов, работающих в подобных режимах. Вспомним, что критический кавитационный запас рассчитывается по выражению (5)

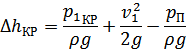
В этом выражении в правой части записана разница пьезометрических напоров во входном сечении насоса и в сечении, где давление минимально (у кромок лопаток)

Если пренебречь разницей уровней этих сечений, то разница пьезометрических напоров, будучи равной разности статических напоров, пропорциональна скорости жидкости во второй степени

Поэтому

Для двух насосов

Слайд 9

Уравнение (22) позволяет определить критический кавитационный запас насоса, геометрически подобного другому насосу, кавитационные свойства которого известны. Или же пересчитать критический кавитационный запас насоса с одной скорости вращения на другую. Приведенная формула справедлива для всех видов насосов, имеющих вращающиеся рабочие органы или циклический рабочий процесс.

Выразим в (18) и (22) линейный размер L.

Приравняем правые части

Возведем обе части в степень 3/2

Слайд 10

Соберем n в левой части уравнения и преобразуем ее

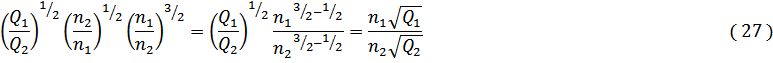
Получилось уравнение

Разделим левую часть на правую и умножим обе части на 10^3/4

Следовательно, величина

одинакова для всех геометрически подобных насосов при их работе на подобных режимах. По аналогии с коэффициентом быстроходности насоса ее называют кавитационным коэффициентом быстроходности. Уравнение было получено С.С. Рудневым. Из него следует, что кавитационные свойства насоса тем выше, чем больше С. При работе в оптимальном режиме насосов, плохих в кавитационном отношении (например насосов для загрязненных жидкостей), кавитационный коэффициент быстроходности для первого критического режима C ₁ = 600-700 и меньше, для обычных насосов С₁ = 800-1000, для насосов с повышенными кавитационными свойствами С₁ = 1300 и более. Эти коэффициенты определены при подстановке в формулу (30) подачи (м³/с), скорости вращения (мин^–1), 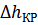(м).

Уравнение (30) позволяет определить критический кавитационный запас или, при известном критическом кавитационном запасе, максимальную скорость вращения, если известен коэффициент С.

[1] БАШТА Т.М., РУДНЕВ С.С., НЕКРАСОВ Б.Б. Гидравлика, гидромашины и гидроприводы (1982)