Зависимость скорости реакции от температуры
Скорость химических реакций с повышением температуры резко растет. Для гетерогенных реакций температурный коэффициент скорости обычно ниже, чем для гомогенных, так как при этом накладывается влияние других факторов, и наиболее медленной стадией процесса является не сама химическая реакция, а процессы диффузии, адсорбции и т.п. Зависимость скорости гомогенной реакции от температуры приближенно описывается эмпирическим правилом Вант-Гоффа: при нагревании на 10° скорость реакции увеличивается в 2-4 раза, т.е.
(kt+10)/k = 2 ÷4 = γ
где kt+10 — константа скорости при температуре t + 10°; kt - константа скорости той же реакции при температуре t°.
Отношение (kt+10)/k называется температурным коэффициентом и обозначается γ. Определив γ, можно приближенно рассчитать константу скорости при любой температуре по уравнению
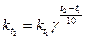
(в небольшом интервале температур). Правило Вант-Гоффа применяется для ориентировочных расчетов. Более точно зависимость скорости реакции от температуры описывается уравнением Аррениуса:
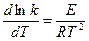
где k — константа скорости реакции; Т — температура, °К; R — yниверсальная газовая постоянная; Е — эмпирическая постоянная, имеющая размерность энергии (энергия активации). После интегрирования уравнение принимает вид
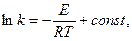
а в экспоненциальной форме
k = Ae-E/RT
где А — эмпирическая постоянная, называемая предэкспоненциальным множителем.
Условием протекания реакции является столкновение молекул, однако еще Аррениус указал, что не каждое столкновение молекул приводит к химическому взаимодействию. Это объясняется следующими обстоятельствами:
1. Число соударений в газовой фазе очень велико (порядка 1028 в 1 см3/сек при обычных условиях, т.е. при р = 1 атм и t = 25°С), поэтому если бы все столкновения кончались взаимодействием, все реакции проходили бы со скоростью взрыва.
2. Скорости однотипных реакций должны бы были быть одинаковыми, но это противоречит действительности, так как скорость зависит от природы реакции.
3. Зависимость скорости реакции от температуры должна была бы быть меньшей, так как число соударений согласно молекулярно-кинетической теории пропорционально корню квадратному из значения абсолютной температуры. Поэтому увеличение числа столкновений при нагревании на 10° может повышать скорость максимально на 2%, но не на 100-200%, как наблюдается в действительности.
4. Влияние катализаторов на скорость реакции при этом остается необъяснимым.
Таким образом, к реакции должны приводить лишь эффективные столкновения частиц, число которых составляет малую долю от общего числа столкновений. Эффективными будут столкновения между активными частицами. Аррениусу не удалось объяснить природу активных молекул и смысл предэкспоненциального множителя А. Молекулярно-кинетическое истолкование уравнения Аррениуса было дано Алексеевым, который предложил активными считать молекулы, обладающие повышенным запасом энергии.
Энергией активации реакции называется минимальная энергия (в расчете на 1 г-моль), которой должны обладать реагирующие частицы, чтобы столкновение между ними привело к реакции. Частицы, энергия которых больше или равна Е, называются активными. Эта энергия необходима для преодоления энергетического барьера реакции, т.е. по современным представлениям, для преодоления энергии отталкивания электронных облаков сталкивающихся молекул. Столкновение будет эффективным, если суммарная величина энергии сталкивающихся частиц равна или больше энергии активации Е, характерной для данной реакции. Если реакция сложная (протекает несколько стадий), то параметр Е в уравнении Аррениуса не имеет простого физического смысла и представляет некоторую функцию энергий активации отдельных стадий или вообще эмпирическую величину. Однако и при этом параметр Е обычно называют энергией активации, хотя правильнее называть его эффективной или эмпирической энергией активации. К активным относятся все молекулы, скорости движения которых равны или больше некоторой величины (обычно доли процента от общего числа молекул). С повышением температуры доля активных молекул возрастает, следовательно, и скорость реакции с повышением температуры будет возрастать.
Энергия активации характеризует зависимость скорости реакции от температуры. Чем больше энергия активации, тем быстрее увеличивается с ростом температуры скорость реакции. Для разных реакций, имеющих близкие значения предэкспоненциального множителя А, константы скорости при данной температуре тем больше, чем меньше энергия активации.
Стерический фактор. Согласно теории соударений, предэкспоненциальный множитель А (эмпирическая постоянная в уравнении Аррениуса) представляет собой фактор соударений, т.е. вероятность соударения друг с другом в течение 1 сек двух частиц, находящихся в объеме 1 см3. Полное число двойных соударений z связано с фактором соударений z0 соотношением
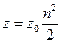
где n — число частиц в 1 см3.
Величины z и z0 могут быть определены на основании молекулярно-кинетической теории. Поэтому заменив А на z0, константу скорости можно рассчитать по уравнению
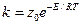
Однако такой расчет скорости реакции часто дает завышенные результаты, особенно для реакций в растворах. Для согласования расчетных данных с опытными в уравнение вводят дополнительный множитель Р, называемым стерическим или вероятностным фактором:
k = Pzne-E/RT
Следовательно,
A = Pza
Стерический фактор Р зависит от природы реакции и может изменяться в пределах от 1 до 10-8; для некоторых ионных реакций, протекающих в растворах, стерический фактор может быть больше единицы. Согласно теории соударений, стерический фактор учитывает вероятность того, что при столкновении частицы будут обладать необходимой для протекания реакции пространственной ориентацией. Отсюда произошло и название этого множителя. Однако теория соударения не позволяет рассчитать предэксноненциальный множитель и стерический фактор. Предэкспоненциальный множитель может быть определен лишь экспериментально в результате измерения констант скорости при нескольких температурах. Вычислив энергию активации, можно по значению k при некоторой температуре рассчитать Р.
Вопрос о возможности теоретического расчета скоростей реакций (без экспериментального их изучения) на основании свойств реагирующих молекул решается теорией абсолютных скоростей реакций (или теорией переходного состояния). Основная идея состоит в том, что промежуточным состоянием любого элементарного акта химического превращения является образование активированного комплекса. Согласно этой теории активированный комплекс представляет собой особого рода неустойчивую молекулу с очень малой продолжительностью жизни. Распад его с образованием продуктов реакции происходит с частотой, независимой от его природы и определяемой только температурой. Согласно теории переходного состояния, стерический фактор может быть рассчитан по выражению
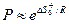
где ΔS+ —энтропия активации, т.е. изменение энтропии при образовании одного моля активированных комплексов в стандартных условиях (при концентрациях активированного комплекса и исходных частиц, равных 1 моль/л); R — газовая постоянная.
Название «стерический фактор» не отражает физического смысла, так как этот множитель определяется не геометрической вероятностью, как предполагалось теорией соударений, а вероятностью благоприятной ориентации внутримолекулярных движений, которая приводит к замене части вращательных степеней свободы колебательными. Наблюдаемые в действительности низкие значения стерического фактора обусловлены затруднениями в передаче энергии от одной степени свободы молекулы к другой при образовании активированного комплекса. Поэтому правильнее называть этот множитель энтропийным или вероятностным фактором. Таким образом, теория переходного состояния позволяет вычислить предэкспоненциальный множитель, если известна конфигурация реагирующих молекул в переходном состоянии. Но в большинстве случаев строение активного комплекса и его свойства бывают неизвестными, поэтому расчеты здесь затруднительны и ограничены. Теория переходного состояния позволяет также более строго определить понятие энергии активации.
Истинной энергией активации элементарного акта химического превращения называется минимальная энергия, которой должна обладать исходная система сверх своей нулевой энергии, чтобы в ней могло произойти рассматриваемое химическое превращение. Энергия активации равна разности нулевых энергий переходного и исходного состояний системы. Из этих определений следует, что разность истинных энергий активации обратной и прямой реакции равна тепловому эффекту реакции при абсолютном нуле.
Энергия активации Е (эффективная энергия активации) определяется на основании эспериментальных данных.
Способы расчета энергии активации.
1. Интегрирование уравнения Аррениуса в пределах от Т1 до Т2 дает уравнение
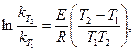
из которого можно рассчитать энергию активации Е по константам скоростей при двух температурах.
2. Построение графика зависимости lg k от 1/Т, соответствующей предыдущему уравнению, когда известен ряд констант скоростей при разных температурах. Из тангенса угла наклона прямой к оси абсцисс (1/Т) рассчитывают Е по формуле:
Е = - 2,3*R* tg φ
3. Вычисление по основному уравнению теории соударений
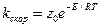
Этот путь возможен только для немногих простейших бимолекулярных реакций, для которых Р = 1.
Зная значение kскор для одной какой-либо температуры и рассчитав z0, можно определить Е.








