II. Дифференциальные методы. Эти методы основаны на использовании уравнения для скорости реакции в его дифференциальной форме.
1. Метод Вант-Гоффа состоит в том, что реакцию проводят с компонентами, взятыми при двух различных исходных концентрациях С1 и С2. Тогда
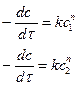
Уравнения делят друг на друга и логарифмируют:
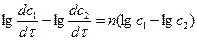
откуда
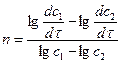
или
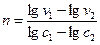
где V1и V2 —скорости реакции с различными начальными концентрациями реагентов C1 и C2.
2. Графические варианты метода Вант-Гоффа основаны на использовании уравнения
lgV = lgk + nlgC
которое получается при логарифмировании выражения для скорости реакции n-го порядка
V=kCn
На графике в координатах lg V — lg C полученная зависимость изображается прямой линией с наклоном к оси lg C, соответствующим порядку реакции (tg φ = n). Отрезок, отсекаемый на оси lg V, равен lg k. Скорость определяется тангенсом угла наклона касательной к кривой С = f (t) относительно оси времени, т.е. графическим дифференцированием. В зависимости от того, какая определяется скорость — в начальный момент реакции или в различные промежутки времени от начала реакции - различаются два графических варианта этого метода.
Вариант 1. Определяют начальные скорости реакции при рачличных исходных концентрациях вещества (рис. 32). Для определения начальных скоростей к каждой точке кривой (рис. 32а), соответствующей моменту начала реакции, проводят касательную. Логарифмы полученных начальных скоростей наносят на график lg V = f (lg C) (см. рис. 32б). Наклон полученной прямой соответствует порядку реакции nс, который называют концентрационным или истинным. При таком определении порядка реакции образующиеся промежуточные продукты не могут влиять на скорость реакции.
Вариант 2. Определяют скорость реакции в различные моменты времени от начала реакции, используя данные одного опыта. Затем измеряют тангенсы угла наклона касательных к кинетической кривой при различных значениях t (т.е. определяют скорости, рис. 33а). Тангенс угла наклона прямой на рис. 33б представляет порядок реакции, который, в отличие от концентрационного, называют временным (nt). Данным способом можно обнаружить влияние на скорость реакции промежуточных продуктов, образующихся в ходе реакции.
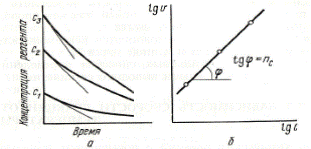
Рис. 32. Определение порядка реакции по методу Вант-Гоффа (вариант I)
Временной и концентрационный порядки реакции могут быть разными, если промежуточные продукты искажают ход реакции, или временной порядок выше концентрационного (nt > nс), т.е. скорость реакции падает со временем быстрее, чем следовало ожидать а основании концентрационного порядка, это означает, что некоторые промежуточные продукты замедляют процесс.
Обратный вывод можно сделать, если временной порядок окажется меньше концентрационного (n t< nс). В таком случае уменьшение скорости реакции со временем меньше ожидаемого, т.е. наблюдается активация процесса продуктами реакции (автокатализ).
При установлении порядка реакции наименее точным является метод определения его по периоду полупревращения. Этот метод дает временной порядок, а изменение времени полупревращения с концентрацией соответствует концентрационному порядку. Следовательно, определяемый таким способом порядок реакции представляет собой среднее между nt и nс. Только при совпадении nt и nс результат определения получается правильным.
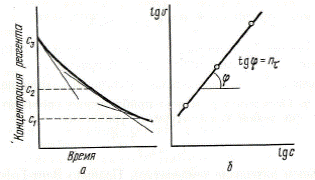
Рис. 33. Определение порядка реакции по методу Вант-Гоффа
(вариант 2): a - кинетическая кривая; б – lg V = f (lgC)
Интегральные методы позволяют определить суммарный временной порядок реакции, а не истинный, так как проводится обработка результатов только одного опыта.
Дифференциальные методы осложняются невозможностью точного определения наклона кривой в данной точке.
Использование всех возможных способов определения порядка реакции делает более надежными выводы об ее кинетике.








