Реакции нулевых порядков. Такой порядок получается при постоянстве скорости реакции, что возможно при поддержании постоянной концентрации исходных веществ.
| 
|
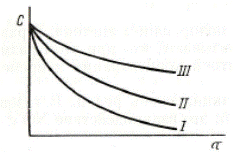
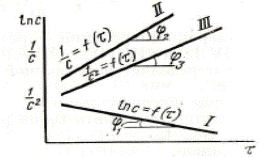
| Рис. 31а. Изменение концентрации исходных веществ во времени для реакций различных порядков: I – реакция первого порядка, II – реакция второго порядка, I II – реакция третьего порядка | Рис. 31б. Зависимость различных функций концентрации исходных веществ от времени для реакций различных порядков |
Нулевой порядок наиболее часто встречается среди гетерогенных реакций.
Сравнение реакций различных порядков представлено на рис. 31. Для реакции n-го порядка (кроме первого) при равенстве концентраций всех исходных веществ константа скорости выражается уравнением
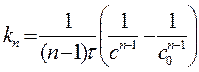
Методы измерения скорости химической реакции. Измерение скорости реакции основано на определении концентрации одного из реагирующих веществ через различные промежутки времени от начала реакции. Для определения концентраций можно применять методы физико-химического анализа, основанные на зависимости физических свойств смеси от ее состава (например, определение показателя преломления, угла вращения или плоскости поляризации, вязкости, электропроводности, объема, плотности, изменения температуры замерзания и температуры кипения, интенсивности окраски и т.д.) и методы аналитической химии (например, титрование). Поскольку концентрации веществ по ходу реакции непрерывно меняются, то необходимо или очень быстрое измерение концентрации (методы физико-химического анализа), или торможение реакции во взятой пробе (химический контроль). Торможение может быть достигнуто охлаждением, резким уменьшением концентрации, устранением катализатора или совместным действием всех указанных факторов. Если реакция, протекающая в газовой фазе, сопровождается изменением числа молекул, то ее течение удобно контролировать по изменению давления смеси во времени.
Среди методов физико-химического анализа для кинетических исследований широко применяются спектроскопия, масс-спектрометрия и хроматография и другие методы.
Большинство из указанных методов может быть применено к сравнительно медленным реакциям, для которых время полупревращения составляет 0,5 часа и более. Для исследования скоростей очень быстрых реакций (с периодом полупревращения до 10-7 и даже 10-9 сек) используются специально разработанные методы анализа и особая аппаратура.
Методы определения порядка реакции. Для определения порядка реакции необходимо иметь экспериментальные данные об изменении концентрации реагирующих веществ со временем. Если в реакции участвует несколько веществ, то пользуются методом изолирования Оствальда. Допустим, в реакцию вступают три вещества А, В и D
аA + bB + сС →
Скорость этой реакции может быть выражена кинетическим уравнением
-dC/dt = k*CAa*CBb*CCc
Сначала проводят реакцию с большими избытками веществ В и С (концентрация вещества А равняется от 0,1 до 0,001 начальной концентрации всех остальных веществ). Тогда
-dC/dt = k1*CAa
где k1 = k*CBb*CCc . При таких условиях определяют а.
Затем проводят второй опыт с большим избытком вещества А и В. Тогда
- dC/ dt = k2*Cсс
где k2 = k * CАа *CBb . При этом определяют с.
Третий опыт проводят с большим избытком веществ А и С и определяют значение в. Таким образом, порядок реакции каждый раз искусственно снижается и сводится к определению частных порядков а, в, с. Общий порядок реакции численно равен сумме а+в+с. Все известные методы определения частных порядков реакций можно разделить на две группы — интегральные и дифференциальные методы.
Интегральные методы. Здесь используются кинетические уравнения для скорости реакции в интегральной форме (полученные после интегрирования дифференциального уравнения скорости реакции). Разновидности этой группы методов:
1. Метод подбора уравнений основан на подстановке экспериментальных данных по концентрации вещества для каждого момента времени в кинетические уравнения реакций различных порядков. Определяемый порядок реакции соответствует тому уравнению, для которого при различных начальных концентрациях исходных веществ и в различные моменты времени при заданной температуре величина константы скорости будет оставаться постоянной.
2. Графический метод основан на определении такой функции от концентрации, которая на графике зависимости ее от времени дает прямую линию. Для реакций первого порядка (I) такой функцией является lg С (см. рис. 31б); для реакций второго порядка (II) 1/с (при соА = с0в); для реакций третьего порядка (III) 1/c2, что вытекает из кинетических уравнений.
Если концентрации исходных веществ различны, то для выделения частного порядка реакции по одному из компонентов используется метод изолирования Оствальда с последующим определением порядка реакции по компоненту одним из рассмотренных способов. По наклону полученной прямой на таком графике вычисляют константу скорости реакции k. При СА ≠ СВ для реакции второго порядка зависимость
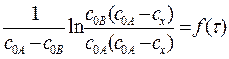
или
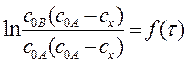
будет выражаться прямой. И в этом случае наклон полученной прямой также характеризует константу скорости.
3. Метод определения по периоду полупревращения, в течение которого исходная концентрация вещества уменьшается вдвое. Для реакции первого порядка время превращения половины (или определенной доли) вещества не зависит от начальной концентрации
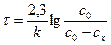
при Сх = СО/2, t = t /2 (время полупревращения)
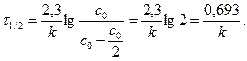
Для реакции второго порядка это время обратно пропорционально начальной концентрации исходного вещества
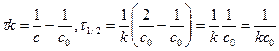
Для реакции третьего порядка
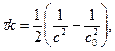
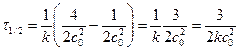
Для реакции n-го порядка соотношение между временем разложения половины исходного вещества и начальной концентрацией будет
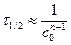
где t1/2 — время полупревращения; C0 — начальная концентрация; n — порядок реакции.
Опыты проводят при двух различных начальных концентрациях CO(1) и CO(2) (при этом все исходные вещества берут в эквивалентных количествах или используют метод изолирования Оствальда):
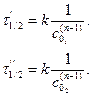
Эти два уравнения делят друг на друга и логарифмируют, откуда
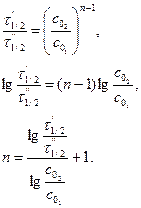
Те же соотношения сохраняются и в случае определения времени разложения любой доли исходной концентрации (т.е. не обязательно определять t1/2, можно определить, например, t1/3 или t1/4). Этот метод называют иногда методом Оствальда — Нойеса.








