Количественная зависимость, устанавливаемая между адсорбентом и адсорбтивом при постоянной температуре в виде уравнения или кривой, называется изотермой адсорбции.

Дата: 2025-06-14; Просмотры: 1

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Cуществует несколько типов изотерм адсорбции - простейшими уравнениями для описания адсорбции являются уравнение Фрейндлиха и уравнение Ленгмюра.

Изотерма адсорбции по Фрейндлиху. Адсорбция растворенного вещества на твердой поверхности подчиняется определенной закономерности, согласно которой концентрация адсорбированного вещества возрастает не пропорционально его концентрации в растворе, а значительно медленнее, и пропорциональна корню n-ой степени из концентрации раствора. Эта зависимость при постоянной температуре может быть представлена следующем уравнением:

Х/ m = К С^{1/ n}

где Х – количество (моль) вещества, адсорбированного m г адсорбента: С- равновесная концентрация; К и 1/n – эмпирические константы, характерные для данных адсорбента и адсорбата, значение 1/n колеблется между 0,1 – 0,7. Данное уравнение известно под названием изотермы адсорбции и имеет вид параболы.

Для графического построения изотермы адсорбции по Фрейндлиху на оси абсцисс откладывается равновесная концентрация в ммоль/л, а на оси ординат – величина адсорбции на единицу поверхности Х/m в ммоль/грамм. На рисунке 14 показано графическое изображение уравнения Фрейндлиха.

Логарифмируя данное уравнение, можно найти значения постоянных К и 1/n:

lg X/m = lg K + 1/n lg C

Если на абсциссе отложить величину lgC, а на ординате – величину lgX/m, то мы получаем прямую, отсекающую на оси ординат отрезок, равный lgК, а тангенс угла наклона этой прямой к абсциссе дает значение 1/n.

Графически значение 1/n находят следующим образом: из точки lgС = 1 восстанавливают перпендикуляр к прямой. Из точки пересечения опускают перпендикуляр на ось ординат – точка lgХ¹.

Величина 1/n будет равна разности (lgХ¹ - lgК), где lgХ¹ –ординаты точки, абсцисса которой lgС₁ = 1 (рис.15). Уравнение Фрейндлиха находит широкое применение, но имеет и ряд недостатков, т.к. применимо только в области средних концентраций.

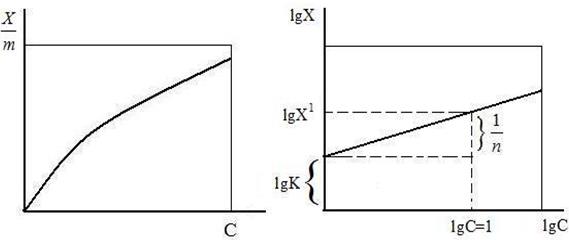Рис.14. Изотерма адсорбции по Фрейндлиху Рис.15. Графическое определение постоянных адсорбции уравнения Фрейндлиха