Задание 2. Определение теплового эффекта реакции окисления
металлического цинка и восстановления ионов меди в водном растворе
Тепловые эффекты реакций измеряются так же, как и постоянная калориметра. Тепловой эффект вычисляется по уравнению
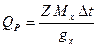
Исследуемая реакция является окислительно-восстановительной, и механизм её заключается в переносе электронов от металлического цинка к ионам меди согласно уравнению
Cu2+ + Zn0 = Cu0 + Zn2+ + Qp
Измеряемый тепловой эффект будет равен Qp = DH. Данный процесс необратим, т.к. цинк, переходя в раствор, не восстанавливается, и реакция идет до полного исчезновения ионов меди в растворе с эквивалентной заменой их на ионы цинка.
В стакан Б калориметра наливают 400 мл 0,05 М раствора медного купороса (CuSО4×5H2O). Закрывают сосуд А так, чтобы нижние концы термометра и мешалки не доставали дна стакана Б на 1 – 2 см. Включают мотор мешалки и измеряют температуру, точно следуя тем записям, которые проводились при измерении водяного числа (постоянной калориметра). На 11-й минуте через воронку В в стакан Б высыпают 3 г цинковой пыли.
Данные заносят в таблицу 4. По полученным данным строят график изменения температуры и находят Dt (рис.3).
Тепловой эффект реакции рассчитывают по уравнению
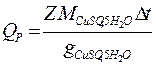
где g CuSO 4 5 H 2 O – количество кристаллогидрата, содержащегося в 400 мл 0,05 М раствора.
Тепловой эффект химической реакции является следствием изменения внутренней энергии реагирующих веществ, и без воздействия внешних сил на условия протекания реакции внутренняя энергия полностью превращается в теплоту. Если эта реакция осуществляется в гальваническом элементе, то часть внутренней энергии будет превращаться в полезную работу. Эта работа будет максимальной, когда химический или физический процесс протекает изотермически и обратимо. Именно этим условиям соответствуют процессы, протекающие в гальванических элементах. Реакция окисления Zn и восстановления Cu2+ наблюдается в элементе Даниэля - Якоби:
Cu | Cu2+ | KCl | Zn2+ | Zn
Максимальная работа по перенесению заряда равна (Дж×моль-1)
W = n × F × E
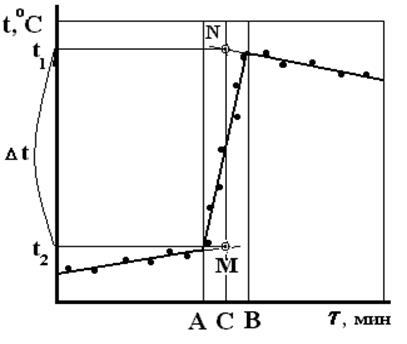
Рис.3. Графическое определение Dt для вычисления теплового эффекта
реакции.
где n – число переносимых электронов, F – число Фарадея (96500 Кл), E – электродвижущая сила (1,10 В). Максимальная работа равна, но противоположна по знаку изменению свободной энергии DG. Следовательно, DG процесса можно рассчитать по уравнению
W = – DG
Свободная энергия является частью энтальпии и связана с ней соотношением DG = DH – T×DS, где T×DS – связанная энергия. Зная DH и DG, можно рассчитать энтропию окисления цинка и восстановления ионов меди по уравнению
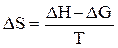
где Т – температура, при которой проводился эксперимент (температура окончания реакции окисления Zn с точностью до 10). При расчете DS следует свободную энергию (DG) и тепловой эффект реакции (DH) привести в единую систему измерения величин, т.е. тепловой эффект, рассчитанный в калориях перевести в джоули (1 калория = 4,18 Дж). Результаты вычислений заносят в таблицу 5.
Таблица 3
Определение постоянной калориметра (Z). Масса KCl 7,2 г
| Периоды, мин | |||||
| Предварительный | Главный | Заключительный | |||
| Время, мин | Т, оС | Время, мин | Т, оС | Время, мин | Т, оС |
| 0 1 2 3 4 5 6 7 8 9 10 | 10,5 11 11,5 12 12,5 13 13,5 14 14,5 15 | 16 17 18 19 20 21 22 23 24 25 26 | |||
Таблица 4
Определение теплового эффекта реакции
| Периоды, мин | |||||
| Предварительный | Главный | Заключительный | |||
| Время, мин | Т, оС | Время, мин | Т, оС | Время, мин | Т, оС |
| 0 1 2 3 4 5 6 7 8 9 10 | 10,5 11 11,5 12 12,5 13 13,5 14 14,5 15 | 16 17 18 19 20 21 22 23 24 25 26 | |||
Таблица 5.
Результаты вычислений
| Опыт | Dt, OC | Z | QP, ккал/моль | DG, кДж/моль | DS, Дж/моль*К |
| Определение Z | ___ | ___ | |||
| Определение QP | ___ |
2. ОПРЕДЕЛЕНИЕ ЭЛЕКТРОДНЫХ ПОТЕНЦИАЛОВ И КОНЦЕНТРАЦИИ ИОНОВ В РАСТВОРЕ МЕТОДОМ ИЗМЕРЕНИЯ ЭЛЕКТРОДВИЖУЩИХ СИЛ
При известных условиях электрическая энергия может быть получена за счет всех видов энергии: механической, тепловой, световой и т.д. Очень часто электрическую энергию получают за счет химических превращений.
Прибор, в котором в результате химических реакций получается электрическая энергия, т.е. химическая энергия превращается в электрическую энергию, называется гальваническим элементом.
Гальванические элементы нашли широкое применение в качестве источников постоянного тока в промышленности, на транспорте, в военном деле, в лабораторной практике, в медицине и других областях народного хозяйства и науки.
Гальванический элемент состоит из двух или нескольких полуэлементов или электродов. Простейший электрод (первого рода) представляет собой металлическую пластинку, погруженную в раствор, содержащий ионы этого же металла.
Еще в XVIII веке было замечено, что на границе раздела металл-вода (или раствор электролита) возникает разность электрических потенциалов.
По современным представлениям, при погружении металла, например, цинка, в воду происходит отрыв ионов от кристаллической решетки металла под влиянием полярных молекул растворителя. В результате перехода катионов металла в раствор металл приобретает некоторый отрицательный заряд за счет оставшихся на нем электронов. Возникающий отрицательный заряд будет во все большей степени препятствовать переходу положительных ионов цинка в раствор. Наконец, растворение металла прекратиться вообще, точнее, между пластинкой металла и раствором установиться динамическое равновесие – скорость растворения металла станет равной скорости обратного процесса осаждения катионов цинка из раствора на пластинку. Это равновесие, состояние которого определяется природой металла и растворителя, обуславливает появление двойного электрического слоя и определенный скачок потенциала между металлом и растворителем, получивший название электродного потенциала. В случае цинкового электрода протекают две равновесные реакции:
Zno – 2 e = Zn +2
Zn +2 + 2 e = Zn o
У разных металлов, вследствие неодинаковой энергии связи атомов в кристаллической решетке и различной способности их катионов к гидратации, растворение металла протекает не в одинаковой степени, а, следовательно, и равновесные электродные потенциалы, возникающие на границе металл-жидкость, будут различными. Так же на величину равновесного потенциала будет оказывать концентрация одноименных с металлической пластинкой ионов.
Это связано с тем, что присутствующие в растворе ионы цинка будут способствовать сдвигу равновесия в сторону увеличения скорости осаждения ионов цинка из раствора на пластинку, тем самым, уменьшая отрицательный заряд пластинки. Заряд пластинки будет тем меньше, чем больше концентрация ионов цинка в растворе.
Таким образом, при погружении металлической пластинки в водный раствор, содержащий ионы того же металла на границе раздела фаз возникает двойной электрический слой, обусловленный конкуренцией двух процессов:
а) растворение металла, характеризуемое работой, затрачиваемой на вырывание протонов из кристаллической решетки металла и перевода их в раствор;
б) осаждение ионов на металлическую пластинку, определяемое работой по разрушению гидратной оболочки ионов и осаждению их на металле.
Если энергия гидратации больше энергии электронно-ионной связи металла, то ионы выходят из металла в раствор, пластинка заряжается отрицательно, а близлежащий слой раствора – положительно.
Если энергия гидратации меньше энергии электронно-ионной связи металла, то ионы осаждаются на пластинке, она заряжается положительно, а близлежащий слой раствора – отрицательно.
Если гальванические цепи составляются из двух качественно различных электродов с различными активностями ионов, то они называются химическими и схематически это записывается следующим образом:
M1| 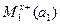 |электролитический|
|электролитический| 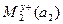 |M2
|M2
e1 проводник e2
где а1 и а2 – активности ионов в растворе; вертикальные черточки представляют границу раздела металл-раствор, причем электрод с большим потенциалом (восстанавливается) записывается справа, а с меньшим (окисляется) - слева.
Электролитический проводник включают для устранения диффузионного потенциала, который возникает на границе электродных электролитов, либо за счет различной подвижности ионов, либо за счет разницы концентраций. При этом электролитический проводник должен удовлетворять следующим требованиям:
· электролит должен быть сильным;
· концентрация электролита должна быть высокой;
· электролитические подвижности ионов должны иметь близкие значения ( 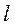 катиона =
катиона = 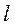 аниона);
аниона);
· электролит не должен образовывать труднорастворимое соединение с электродными растворами.
Примером гальванического элемента может служить медно-цинковый элемент Даниэля-Якоби, состоящий из двух электродов первого рода – медного и цинкового. Электроды представлены медной и цинковой пластинками, погруженными соответственно в растворы сульфата меди и сульфата цинка. Схематически элемент Даниэля-Якоби вглядит так:
Zn | ZnSO 4 || CuSO 4 | С u
Если рассматривать цинковый и медный электроды в отдельности, то, как и описывалось выше, на границах металл-раствор в конкретных условиях сформируются равновесные электродные потенциалы. Однако как только соединить два электрода в электрическую цепь при помощи электрического проводника (провод, не путать с электролитическим проводником), в силу более выраженных металлических свойств цинка, пластинка последнего будет, растворяясь, окисляться, а ионы меди из раствора будут осаждаться на медной пластинке.
Zn + CuSO4 = Cu + ZnSO4
или
Zno + Cu+2 = Zn+2 + Cuo
При этом электроны по проводнику будут двигаться от цинковой пластинки к медной, т.е. в цепи возникнет электрический ток.
Таким образом, комплекс протекающих окислительно-восстановительных реакций, представляющий химическую работу по перераспределению зарядов (в нашем случае между металлическими пластинками и растворами каждого электрода) привел к возникновению разности потенциалов между двумя электродами. Данная максимальная разность потенциалов, характеризующая максимальную работу гальванического элемента, называется электродвижущей силой, или ЭДС.
Е = e 1 – e 2 ,
где Е – электродвижущая сила (ЭДС); e1 и e2 - потенциалы электродов.
В агрохимии, физиологии растений, в почвоведении знание современных методов измерения электродвижущих сил имеет большое значение. Эти методы дают возможность быстро и точно определить кислотность почв и концентрацию водородных ионов в клеточном соке живых организмов. Окислительно-восстановительные и мембранные потенциалы также наиболее надежно определяются измерением электродвижущих сил соответствующих почвенных или физиологических объектов.
Гальванические элементы могут состоять из обратимых или необратимых электродов, соединенных электролитическим проводником. Элемент называется необратимым, если в системе хотя бы один из процессов является необратимым. Обратимый гальванический элемент – это элемент, в котором на границе двойного электрического слоя протекают обратимые окислительно-восстановительные процессы.
Классификация электродов: по своему строению электроды бывают первого и второго рода.
К электродам первого рода относятся электроды, состоящие из металлической пластинки, соприкасающейся с раствором соли того же маталла (медный, цинковый, никелевый и др. электроды) или металл, с растворенным в нем атомами другого элемента, соприкасающийся с раствором ионов этого элемента (амальгамо-кадмиевый, водородный, кислородный, хлорный и др.). Электродный потенциал электродов первого рода зависит от концентрации катионов в растворе, эти электроды называются электродами, обратимыми по катиону.
В качестве примера электрода первого рода выше уже рассматривался цинковый электрод.
Электродный потенциал электрода первого рода определяется уравнением Нернста:
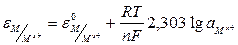 ,
,
где e («эпсилон») - электродный потенциал, В;
e0 – стандартный (нормальный) электродный потенциал, В;
R – универсальная газовая постоянная – 8,31 Дж/моль*К;
Т – абсолютная температура, ºК;
F – число Фарадея – 96500 Кл/моль;
n – количество переданных электронов;
2,303 – модуль перехода от натурального логарифма к десятичному;
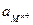 - активность ионов металла в растворе.
- активность ионов металла в растворе.
Активность ионов связана с концентрацией раствора, и эта связь выражается уравнением
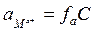
где 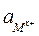 – активность, С – молярная концентрация раствора и
– активность, С – молярная концентрация раствора и 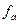 – коэффициент активности, учитывающий электростатическое взаимодействие ионов в растворе.
– коэффициент активности, учитывающий электростатическое взаимодействие ионов в растворе.
Так же к электродам первого рода относится водородный электрод. Он относится к группе газовых электродов, которые состоят из инертного проводника, например платиновой пластинки, насыщенного газом, который обменивается ионами с раствором. Происходящие на водородном электроде химические процессы можно изобразить суммарным равенством:
Н2 ↔ 2Н↔ 2Н+ + 2е
В результате процессов на границе между платиной и раствором образуется двойной электрический слой и возникает электродный потенциал. Величина его при данной температуре определяется с одной стороны, активностью водородных ионов в растворе, а с другой – количеством поглощенного платиной водорода, которое пропорционально его давлению.
Платиновая пластинка, насыщенная водородом под давлением 1 атм. и погруженная в раствор с активностью ионов водорода, равной единице (1М раствор серной кислоты), называется нормальным водородным электродом и схематически записывается так:
Pt, H2| 2H+
По международному соглашению, потенциал нормального водородного электрода условно принят равным нулю. Нормальный водородный электрод играет роль эталона, потому что с его величиной сопоставляют потенциалы других электродов. Электроды, имеющие устойчивый (известный) потенциал и служащие для определения потенциалов других электродов, называются стандартными электродами или электродами сравнения. Нормальный водородный электрод является одним из электродов сравнения. Электродный потенциал водородного электрода можно вычислить по формуле:
εН2 = 0.059 lg a Н2








