Вычисление неопределенных интегралов.

Дата: 2025-06-14; Просмотры: 1

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Функция f(x)	Первообразная F(x)	Пример
0	С
1	х + С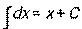
k – (число)	kx + C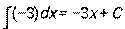
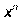
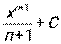
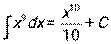
x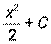
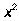
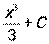
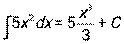
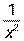
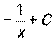
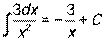
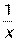
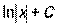
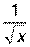
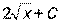
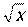
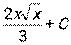
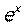
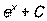
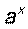
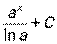
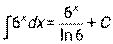
sin x	- cos x +C
cos x	sin x+C
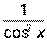
	tg x +C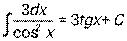
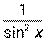
	- ctg x+C

Свойства неопределенных интегралов.

1. 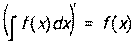. Интегрирование и дифференцирование – взаимно обратные действия.

2. 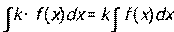. Постоянный множитель можно вынести за знак интеграла.

3. 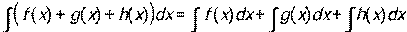. Интеграл суммы нескольких функций равен сумме интегралов этих функций.

4. 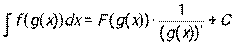. Интеграл сложной функции равен первообразной внешней функции, умноженной на выражение, обратное производной внутренней функции.

5. Интегрирование по частям: .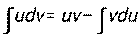

Контрольная работа

по учебной дисциплине: «Математика»

для всех специальностей заочной формы обучения

Вариант 1

1. Даны матрицы: А = 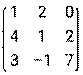и В = .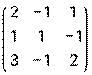

Найти матрицу С = А^т · (В + 2А).

1. Дана система линейных уравнений. Решить ее двумя способами: при помощи формул Крамера и методом Гаусса:
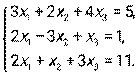
2. Даны уравнение 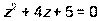и комплексное число .

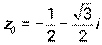а) Решить уравнение и найти его корни 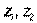на множестве комплексных чисел.

б) Найти комплексное число в алгебраической форме.

в) Получить тригонометрическую и показательную формы числа .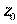

1. Вычислить производную y ′ (х), если. y(х) = ln(sin2x).

1. Вычислить неопределенный интеграл: .
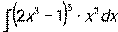2. Найти частное решение дифференциального уравнения с разделяющимися переменными:

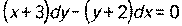, если у = 3 при х = 2.

______________________________________________________________________

Контрольная работа

по учебной дисциплине: «Математика»

для всех специальностей заочной формы обучения

Вариант 2

1. Даны матрицы: А = и В = 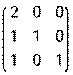. Найти матрицу С = (А – 2В) · А^т.
2. Дана система линейных уравнений. Решить ее двумя способами: при помощи формул Крамера и методом Гаусса:
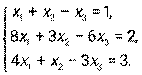
3. Даны уравнение 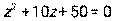и комплексное число .

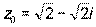а) Решить уравнение и найти его корни 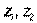на множестве комплексных чисел.

б) Найти комплексное число 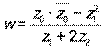в алгебраической форме.

в) Получить тригонометрическую и показательную формы числа .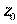

1. Вычислить производную y ′ (х), если .
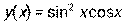2. Вычислить неопределенный интеграл: .
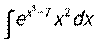3. Найти частное решение дифференциального уравнения с разделяющимися переменными:

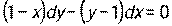, если у = 3 при х = 2.

Контрольная работа

по учебной дисциплине: «Математика»

для всех специальностей заочной формы обучения

Вариант 3

1. Даны матрицы: А = 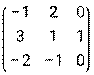и В = 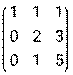. Найти матрицу Р = В ⋅ А + 3А^т .
2. Дана система линейных уравнений. Решить ее двумя способами: при помощи формул Крамера и методом Гаусса:
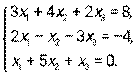
3. Даны уравнение 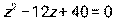и комплексное число .

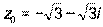а) Решить уравнение и найти его корни 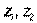на множестве комплексных чисел.

б) Найти комплексное число в алгебраической форме.

в) Получить тригонометрическую и показательную формы числа .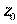

1. Вычислить производную y ′ (х), если .
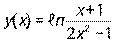2. Вычислить неопределенный интеграл: .
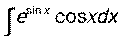3. Найти частное решение дифференциального уравнения с разделяющимися переменными:

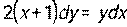, если у = 2 при х = 1.

_________________________________________________________________________

Контрольная работа

по учебной дисциплине: «Математика»

для всех специальностей заочной формы обучения

Вариант 4

1. Даны матрицы: А = и В = .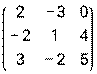

Найти матрицу Р = В^т · (2А – В).

1. Дана система линейных уравнений. Решить ее двумя способами: при помощи формул Крамера и методом Гаусса:
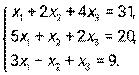
2. Даны уравнение 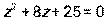и комплексное число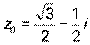

а) Решить уравнение и найти его корни 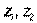на множестве комплексных чисел.

б) Найти комплексное число в алгебраической форме.

в) Получить тригонометрическую и показательную формы числа .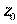

1. Вычислить производную y ′ (х), если .

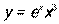1. Вычислить неопределенный интеграл: .
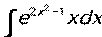2. Найти частное решение дифференциального уравнения с разделяющимися переменными:

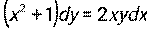, если у = 2 при х = 1.

Контрольная работа

по учебной дисциплине: «Математика»

для всех специальностей заочной формы обучения

Вариант 5

1. Даны матрицы: А = 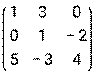и В = .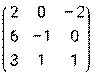

Найти матрицу Т = А ⋅ В + 2А^т;

1. Дана система линейных уравнений. Решить ее двумя способами: при помощи формул Крамера и методом Гаусса:
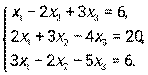
2. Даны уравнение 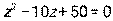, комплексное число .

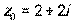а) Решить уравнение и найти его корни 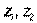на множестве комплексных чисел.

б) Найти комплексное число 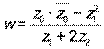в алгебраической форме.

в) Получить тригонометрическую и показательную формы числа .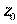

1. Вычислить производную y ′ (х), если .

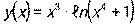1. Вычислить неопределенный интеграл: .
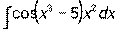2. Найти частное решение дифференциального уравнения с разделяющимися переменными:

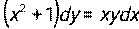, если у = 2 при х = .

__________________________________________________________________________

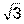Контрольная работа

по учебной дисциплине: «Математика»

для всех специальностей заочной формы обучения

Вариант 6

1. Даны матрицы: А = 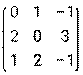и В = .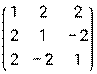

Найти матрицу М = А^т · (2А + В).

1. Дана система линейных уравнений. Решить ее двумя способами: при помощи формула Крамера и методом Гаусса:
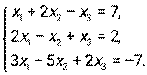
2. Даны уравнение 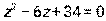и комплексное число .

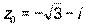а) Решить уравнение и найти его корни 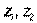на множестве комплексных чисел.

б) Найти комплексное число 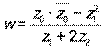в алгебраической форме.

в) Получить тригонометрическую и показательную формы числа .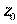

1. Вычислить производную y ′ (х), если .

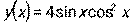1. Вычислить неопределенный интеграл: .
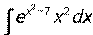2. Найти частное решение дифференциального уравнения с разделяющимися переменными:

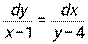, если у = 4 при х = 0.

Контрольная работа

по учебной дисциплине: «Математика»

для всех специальностей заочной формы обучения

Вариант 7

1. Даны матрицы: А = 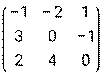и В = .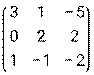

Найти матрицу К = В · А + (В^т - А^т).

1. Дана система линейных уравнений. Решить ее двумя способами: при помощи формул Крамера и методом Гаусса:
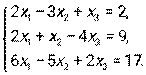
2. Даны уравнение 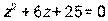и комплексное число .

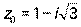а) Решить уравнение и найти его корни 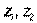на множестве комплексных чисел.

б) Найти комплексное число 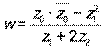в алгебраической форме.

в) Получить тригонометрическую и показательную формы числа .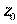

1. Вычислить производную y ′ (х), если .

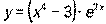1. Вычислить неопределенный интеграл: .
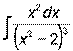2. Найти частное решение дифференциального уравнения с разделяющимися переменными:

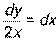, если у = 6 при х = 1.

__________________________________________________________________________

Контрольная работа

по учебной дисциплине: «Математика»

для всех специальностей заочной формы обучения

Вариант 8

1. Даны матрицы: А = 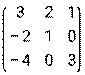и В = .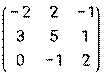

Найти матрицу М = А · В – 2А^т.

1. Дана система линейных уравнений. Решить ее двумя способами: при помощи формулам Крамера и методом Гаусса:

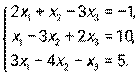
1. Даны уравнение 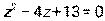и комплексное число .

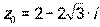а) Решить уравнение и найти его корни 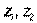на множестве комплексных чисел.

б) Найти комплексное число алгебраической форме.

в) Получить тригонометрическую и показательную формы числа .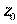

1. Вычислить производную y ′ (х), если .

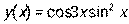1. Вычислить неопределенный интеграл: .
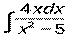2. Найти частное решение дифференциального уравнения с разделяющимися переменными:

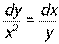, если у = 2 при х = 0.

Контрольная работа

по учебной дисциплине: «Математика»

для всех специальностей заочной формы обучения

Вариант 9

1. Даны матрицы: А = 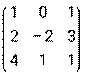и В = 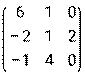. Найти матрицу С = А · В + (А^т – В).
2. Дана система линейных уравнений. Решить ее двумя способами: при помощи формулам Крамера и методом Гаусса:
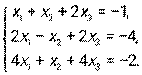
3. Даны уравнение 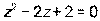и комплексное число .

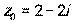а) Решить уравнение и найти его корни 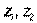на множестве комплексных чисел.

б) Найти комплексное число в алгебраической форме.

с) Получить тригонометрическую и показательную формы числа .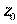

1. Вычислить производную y ′ (х), если .

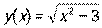1. Вычислить неопределенный интеграл: .
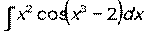2. Найти частное решение дифференциального уравнения с разделяющимися переменными: 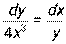, если у = 1 при х = 0.

_____________________________________________________________________

Контрольная работа

по учебной дисциплине: «Математика»

для всех специальностей заочной формы обучения

Вариант 10

1. Даны матрицы: А = 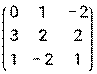и В = 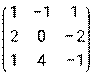. Найти матрицу К = 3В^т - А · В.
2. Дана система линейных уравнений. Решить ее двумя способами: при помощи формулам Крамера и методом Гаусса:
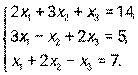
3. Даны уравнение 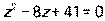, комплексное число .

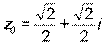а) Решить уравнение и найти его корни 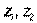на множестве комплексных чисел.

б) Найти комплексное число алгебраической форме.

в) Получить тригонометрическую и показательную формы числа .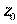

1. Вычислить производную y ′ (х) , если .
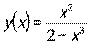2. Вычислить неопределенный интеграл: .
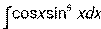3. Найти частное решение дифференциального уравнения с разделяющимися переменными: 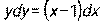, если у = 4 при х = 0.