Теплотехнический расчет красильной машины периодического действия
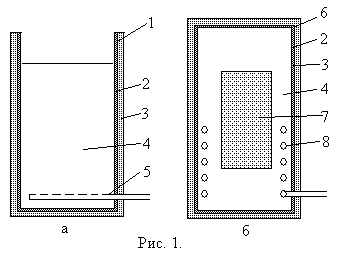 На рис. 1 схематически представлена двухкорпусная установка для периодического крашения. Первый корпус 1 (открытый приготовительный бак), показанный на рис.1а, предназначен для приготовления (разварки) раствора красителя. Он включает в себя корпус 2, тепловую изоляцию 3, залитый раствор 4 и перфорированную трубу 5 для подачи пара (обогрев острым паром). После заливки раствора красителя в бак подается острый пар и производится разогрев красителя от начальной температуры t1 до температуры t2, близкой к температуре насыщения раствора. Нужно заметить, что по мере приближения температуры раствора к температуре насыщения интенсивность процесса конденсации пара резко снижается, и часть подаваемого пара может выходить через поверхность уровня жидкости. Естественно, что такой режим работы с проскоком пара не рационален и его следует избегать, сохраняя конечный недогрев раствора до температуры насыщения порядка 10С. После разогрева процесс разварки красителя продолжается в стационарном режиме определенное время, предусмотренное технологической картой.
На рис. 1 схематически представлена двухкорпусная установка для периодического крашения. Первый корпус 1 (открытый приготовительный бак), показанный на рис.1а, предназначен для приготовления (разварки) раствора красителя. Он включает в себя корпус 2, тепловую изоляцию 3, залитый раствор 4 и перфорированную трубу 5 для подачи пара (обогрев острым паром). После заливки раствора красителя в бак подается острый пар и производится разогрев красителя от начальной температуры t1 до температуры t2, близкой к температуре насыщения раствора. Нужно заметить, что по мере приближения температуры раствора к температуре насыщения интенсивность процесса конденсации пара резко снижается, и часть подаваемого пара может выходить через поверхность уровня жидкости. Естественно, что такой режим работы с проскоком пара не рационален и его следует избегать, сохраняя конечный недогрев раствора до температуры насыщения порядка 10С. После разогрева процесс разварки красителя продолжается в стационарном режиме определенное время, предусмотренное технологической картой.
Теперь приготовленный раствор красителя готов к заливке в закрытый красильный бак 6 (см. рис. 1б). Этот бак содержит те же элементы 2, 3, и 4, что и открытый бак. Кроме того, в нем предусмотрен змеевик 8 и загружается окрашиваемый материал 7. Далее закрытый бак вакуумируется, чтобы избежать защемления пузырьков воздуха в волокнистом материале при заливке раствора, что может вызвать непрокрас. После этого подогретый в приготовительном баке раствор красителя перекачивается в зарытый красильный бак и производится подогрев раствора до температуры tк, превышающей температуру насыщения при атмосферном давлении за счет подачи пара повышенного давления в змеевик. Давление в баке при этом растет и превышает атмосферное. За прогревом в течение определенного промежутка времени следует непосредственно процесс крашения в стационарном режиме. По его окончании систему нужно расхолодить, чтобы понизить давление в баке. Для этого в змеевик подается холодная вода. После понижения температуры крышка бака открывается, материал выгружается и отработанный раствор сливается. На этом заканчивается цикл работы рассмотренной установки.
1. Стадия подогрева раствора красителя в приготовительном баке
На стадии разогрева раствора в приготовительном баке теплота затрачивается на разогрев самого раствора, жидкости Q*ж, разогрев стенок бака, его конструкции Q*к, разогрев материала изоляции Q*из. При разогреве имеют место также потери теплоты через стенки сосуда и тепловую изоляцию в окружающую среду Q*окр, а также потери теплоты через открытую поверхность жидкости Q*пов, обусловленные испарением и теплоотдачей в окружающий воздух. Заметим, что для определения количества теплоты используется обозначение Q* в отличие от обозначения потока теплоты Q. Таким образом, общее количество затраченной теплоты на процесс разогрева определяется суммой перечисленных составляющих
Q*затр = Q*ж + Q*к+ Q*из+ Q*окр+ Q*пов (1)
Затраты теплоты на разогрев жидкости рассчитываются по ее массе Мж
Q*ж=Мжсж(t2 - t1) (2)
где сж – средняя удельная массовая теплоемкость жидкости в интервале температур от начальной t1 до конечной t2.
Пока еще не ясно, какое значение массы жидкости используется в этом уравнении - начальное или конечное, поскольку масса жидкости в баке изменяется за счет конденсации пара. Этот вопрос буде решен ниже при расчете массы пара, затрачиваемой в процессе разогрева.
Значение числа Био Bi= a d / l для металлической стенки бака мало по сравнению с 1 (проверьте) из-за ее малой толщины и относительно высокого коэффициента теплопроводности стали. Это позволяет рассматривать температурное поле в стенке бака как однородное. Кроме того, в соответствии с законом теплоотдачи применительно к внутренней поверхности бака tж- tс= q/a из-за относительно высокого значения коэффициента теплоотдачи a и сравнительно низкого значения плотности потока тепла q через стенку (почему?) температура поверхности стенки tс лишь незначительно отличается от температуры жидкости tж в баке. Эта цепочка рассуждений позволяет сделать вывод о том, что стенка бака целиком имеет ту же температуру, что и жидкость и прогревается вместе с ней. Таким образом, количество теплоты, затрачиваемое на разогрев конструкции, можно представить в форме аналогичной уравнению (2)
Q*к=Мкск(t2 - t1) (3)
Температура изоляции в процессе разогрева изменяется от начального значения t1 до некоторого среднего значения. Благодаря тому, что температурное поле в изоляции практически линейно это значение равно полусумме из значений температур ее поверхности и стенки бака, совпадающей с температурой жидкости. Расчет затрат теплоты на разогрев изоляции, как ясно будет из результатов расчета, дает незначительный вклад в величину Q*затр, определяемую формулой (1). Это дает основание приближенно принять температуру поверхности изоляции в конце разогрева равной ее начальной температуре. При этом изоляция в среднем прогреется на величину dt = (t2 - t1)/2. Тогда затраты теплоты на разогрев изоляции можно будет представить приближенной формулой
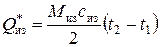 . (4)
. (4)
Такой поход позволяет рассчитывать прогрев изоляции по формулам аналогичным формулам (2 - 3), но с уменьшенной вдвое общей теплоемкостью.
В приведенных уравнениях (3 - 4) масса частей системы рассчитывается по единой формуле
M = rV. (5)
Ввиду того, что стенка бака и изоляции тонкие, их можно рассчитывать по формулам для плоской стенки как произведение площади поверхности на толщину
Vк=p(d12/4+d1H)dк ;
Vиз=p(dиз2/4+dсрH)dиз; (6)
dср = (dиз+ d2)/2,
где d1 и d2 – внутренний и наружный диаметры бака; dср и dиз – средний и наружный диаметры изоляции.
В верхних двух формулах (6) первое слагаемое в скобках учитывает площадь днища, второе – площадь боковой стенки.
Потери теплоты в окружающую среду обусловлены теплопередачей от жидкости к окружающему воздуху через стенки бака и изоляцию
Q*окр = k(átжñ -tв)Ft, (7)
где k – коэффициент теплопередачи; átжñ и tв – средняя по времени температура жидкости и температура воздуха соответственно; F – суммарная площадь боковой поверхности и днища приготовительного бака; t - продолжительность процесса.
Здесь и далее угловые скобки áñ будут использоваться для характеристики средних по времени значений параметров. Поскольку dиз/d1 < 1,5 (убедитесь в этом), то многослойную цилиндрическую стенку можно рассчитывать по формулам для плоской стенки, и величину коэффициента теплопередачи можно представить как
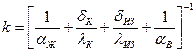 (8)
(8)
Поскольку значение коэффициента теплоотдачи со стороны жидкости существенно выше коэффициента теплоотдачи со стороны воздуха aж>> aв, а термическое сопротивление теплопроводности стенки бака намного меньше термического сопротивления теплопроводности изоляции dк/lк <<dиз/lиз, первыми двумя слагаемыми в знаменателе формулы (8) можно пренебречь и представить величину коэффициента теплопередачи в виде
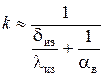 (9)
(9)
Так как вклад потерь тепла в окружающую среду мал (оцените после окончания расчетов), то величиной aв с учетом теплоотдачи свободной конвекцией и излучением можно задаться по порядку величины, приняв aв » 10 Вт/м2К. Температура жидкости в процессе разогрева острым паром изменяется во времени практически линейно, поэтому величину средней температуры жидкости átжñ в формуле (7) можно принять равной среднему арифметическому из начального и конечного ее значений.
В процессе разогрева температура жидкости превышает температуру окружающего воздуха, поэтому теплота с поверхности жидкости теряется как за счет теплоотдачи, так и за счет массоотдачи, испарения жидкости с открытой поверхности. Эта теплота подводится из объема жидкости к ее поверхности. Тепловой баланс для поверхности жидкости при этом можно представить как
qaж = qaв + rj,
или
aж(tж - tп) = aв(tп - tв)+mbr(cп - cв)/(1 -cп), (10)
где qaж и qaв – плотности потоков теплоты за счет теплоотдачи от объема жидкости к ее поверхности и от поверхности жидкости к окружающему воздуху соответственно; j – плотность потока массы с поверхности жидкости в окружающий воздух; r – удельная теплота парообразования; tп – температура поверхности жидкости; m - молярная масса пара; b - коэффициент массоотдачи;
cп и cв - молярные доли паров на поверхности жидкости и в окружающем воздухе.
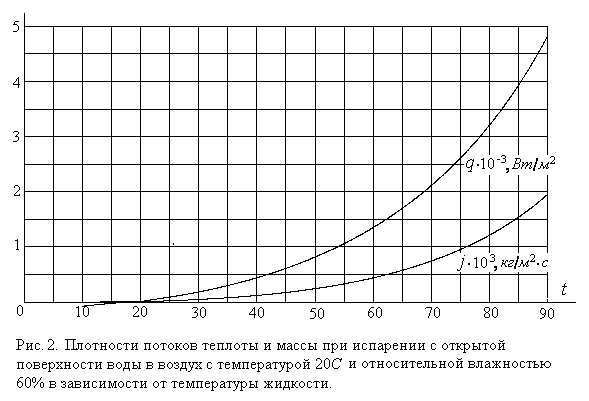
Подробнее о расчете тепломассообмена во влажном воздухе смотрите в соответствующем разделе курса «Тепломассообмен» [4]. Коэффициенты теплоотдачи aж, aв, коэффициент массоотдачи b, молярная доля паров на поверхности cп и удельная теплота парообразования зависят от температуры поверхности нелинейно, и уравнение (10) может быть решено относительно tп с помощью какой либо из итерационных процедур (половинного деления, касательных Ньютона и т.д.). Это позволит найти величину плотности потока теплоты qaж = aж(tж - tп), теряемой жидкостью через поверхность. В задачу данной работы не входит решение уравнения (10) и вычисление плотности потока теплоты. В связи с этим результаты такого решения представлены на рис. 2 графически в виде зависимости плотности потока теплоты от температуры жидкости при постоянных параметрах воздуха: температуре tв = 20С и относительной влажности 60%.
Из-за нелинейного характера представленной на рис. 2 зависимости среднее во времени значение потока теплоты с поверхности жидкости áqповñ более корректно определять не по средней температуре жидкости, а как среднее арифметическое из начального qн(t1) и конечного qк(t2) ее значений
áqповñ = (qн+qк)/2. (11)
После этого по площади поверхности жидкости в баке F и времени t легко рассчитываются потери теплоты через поверхность жидкости
Q*пов = áqповñ F t (12)
Для того, чтобы определить массу пара, затрачиваемого на разогрев системы, запишем уравнение теплового баланса в форме уравнения смешения пара с жидкостью
Mпhп+ (Mж - Mп)cжt1 = Mжcжt2 (13)
где Mп – масса пара, затраченного на разогрев жидкости; hп – энтальпия острого пара, подаваемого в бак.
Левая часть уравнения (13) определяет полные энтальпии компонентов смеси до смешения, причем начальная масса жидкости равна разности конечной массы жидкости и массы сконденсировавшегося пара (Mж - Mп). Правая часть уравнения (13) характеризует полную энтальпию образовавшейся смеси. Уравнение (13) легко преобразовать к виду
Mп (hп - cжt1) = Mж (cжt2 - cжt1) (14)
Анализ процедуры вывода уравнения (14) позволяет сделать вывод о том, что в формуле (2) при расчете затрат теплоты на нагрев жидкости должна использоваться конечная ее масса (после смешения). Тем не менее, ее величина еще не определена, поскольку она должна согласовываться с количеством жидкости, заливаемой в красильный бак, превышая массу последней на 5¸7%. Расчет массы жидкости в красильном баке будет выполнен ниже в разделе 3, при расчете разогрева красильного бака.
Уравнение (14) определяет лишь массу пара, затрачиваемого на разогрев жидкости. Нетрудно заметить, что массу пара, необходимую для разогрева всей системы можно определить по величине суммарных затрат теплоты Q*затр, определяемых уравнением (1)
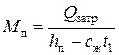 (15)
(15)
Средний по времени расход пара рассчитывается по его массе
áDñ = Mп/t (16)
Рассчитаем теперь количество отверстий в перфорированной трубе. Из-за того, что давление греющего пара в несколько раз превышает давление раствора, истечение из отверстий в трубе будет критическим, а скорость такого истечения можно рассчитать как
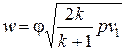
где р – давление греющего пара; v1 – удельный объем подаваемого пара; j - коэффициент скорости; k – показатель адиабаты, равный k = 1,3 для перегретого водяного пара и k = 1,13 для сухого насыщенного или слегка влажного пара.
Коэффициент скорости учитывает отклонение реальной формы отверстия от профилированного суживающегося сопла, а также необратимые потери энергии при истечении, и может быть принят равным j = 0,6. Суммарная площадь отверстий fS в перфорированной трубе определяется по среднему расходу пара и скорости истечения
fS= áDñv1/w
Диаметрами отверстий в перфорированной трубе задаются в интервале 3¸10 мм. Меньшие значения диаметра отверстий способствуют более равномерному диспергированию пара по объему бака и уменьшают вероятность проскока пара через толщу жидкости без конденсации, но зато они легче забиваются в процессе эксплуатации. Вычислив площадь проходного сечения одного отверстия (площадь круга), по суммарному проходному сечению определяют количество отверстий.
2. Установившийся режим работы приготовительного бака
В установившемся режиме разварки красителя определяемые уравнением (1) составляющие затрат теплоты, связанные с разогревом системы, обращаются в ноль, так что за счет подвода пара должны компенсироваться лишь составляющие, обусловленные потерями в окружающую среду через стенки бака и с открытой поверхности жидкости
Q*затр = Q*окр+ Q*пов. (17)
При расчете потерь теплоты в окружающую среду для приближенных оценок можно использовать подход, развитый в предыдущем разделе с заменой в формуле (7) среднего по времени значения температуры на ее конечное значение t2. Следует иметь в виду, что в установившемся режиме потери тепла в окружающую среду Q*окр дают относительно больший вклад в величину Q*затр, чем в режиме разогрева. Для более точного расчета этих потерь следовало бы прибегнуть к итерационной процедуре, учитывающей зависимость коэффициента теплопроводности изоляции от температуры, а также зависимость коэффициента теплоотдачи к окружающему воздуху от температуры поверхности изоляции.
Для определения потерь тепла с поверхности жидкости используется тот же подход, что и в предыдущем параграфе с той лишь разницей, что плотность потока теплоты с поверхности жидкости определяется по графику рис. 2 при установившейся температуре жидкости t2
Также аналогичен и поход к определению массы пара. Расчет ведется по формуле (15)с заменой t1 на t2. Расход пара (постоянный) определяется формулой (16).
3. Разогрев красильного бака глухим паром
В этом расчете ставится задача определения площади поверхности змеевика и определения расхода пара. Затраты теплоты на разогрев этого бака имеют структуру несколько отличающуюся от затрат в приготовительном баке. Поскольку красильный бак закрыт, потери теплоты с поверхности жидкости будут отсутствовать, но появится дополнительная статья расхода тепла, связанная с разогревом окрашиваемого материала Q*м
Q*затр = Q*ж + Q*к+ Q*из+ Q*м + Q*окр (18)
Расчет затрат теплоты на разогрев жидкости выполняется по тому же уравнению (2), что и в приготовительном баке, только следует иметь в виду, что начальная температура t1 для красильного бака равна конечной температуре раствора t2 в приготовительном баке. (Затратами теплоты на разогрев системы при перекачке раствора из приготовительного бака в красильный пренебрегаем).
Чтобы рассчитать величину Q*ж, необходимо предварительно найти массу жидкости, заливаемой в красильный бак. В бак предварительно загружается влажный материал массой Мм с влагосодержанием W . Влагосодержание материала определяется как отношение массы влаги Мвл, содержащейся в материале к массе Мс сухого материала
W = Mвл/Mс (19)
Учитывая, что масса влажного материала складывается из массы сухого материала и массы влаги, нетрудно получить формулу, связывающую массы сухого и влажного материала
Mм=Mс(1+W) (20)
В процессе крашения при загрузке материала должно выдерживаться определенное соотношение между массой материала и массой жидкости (раствора красителя), определяемое модулем ванны m, равным
m = Mж/Mм (21)
При поглощении влаги в малых количествах (при влагосодержаниях не превышающих 0,03) текстильный материал сжимается благодаря действию межмолекулярных сил притяжения. При поглощении значительного количества влаги, что имеет мести и в данном случае, объем влажного материала увеличивается на величину объема поглощенной влаги. Таким образом, объем заливаемой в красильный бак жидкости Vж будет определяться объемом самого бака Vб за вычетом объемов сухого материала Vс и влаги Vвл
Vж = Vб -Vс -Vвл (22)
Выражая объемы жидкости, сухого материла и влаги согласно уравнению (5) через соответствующие массы и плотности и исключая при помощи уравнений (19 ¸ 21) массы влаги, сухого и влажного материала, найдем массу жидкости (раствора), которую необходимо залить в красильный бак
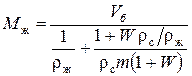 . (23)
. (23)
Масса жидкости, заливаемая в приготовительный бак, до сих пор не определена. При отсутствии потерь жидкости ее можно было бы принять равной величине Mж, рассчитанной по уравнению (23). Учитывая возможные потери и неполноту опорожнения приготовительного бака массу жидкости в нем можно принять с некоторым запасом равной 1,05 Mж, где значение Mж рассчитано по формуле (23).
Затраты теплоты на разогрев влажного материала определяются формулой
Q*м =(Мсcс+ Мвлсж)(t2 - t1),
которая при помощи уравнений (19), (20) легко преобразуется к виду
Q*м =Мм(cс+ Wсж)(t2 - t1)/(1+W), (24)
где cс удельная теплоемкость сухого материала.
Остальные составляющие затрат теплоты в уравнении (18) рассчитываются по тем же формулам, что и в разделе 1, но уже по значениям соответствующих масс (учитывая и массу крышки и изоляции на ней) и температур для красильного бака.
Масса пара, затрачиваемого на разогрев красильного бака глухим паром, рассчитывается по балансному уравнению
Мп = Q*затр/Dh,
где Dh – разность энтальпий греющего пара на входе и выходе из аппарата [5].
Расход пара рассчитывается по массе пара и продолжительности процесса так же, как и в уравнении (16).
Перейдем к определению площади поверхности змеевика. Температурный график встроенного теплообменника-змеевика показан на рис.3.
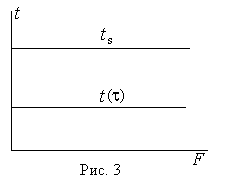 Температура греющей среды – слегка перегретого, сухого насыщенного или влажного пара постоянна как по поверхности змеевика, так и во времени и представляет собой температуру насыщения ts, определяемую давлением пара. Температура раствора t постоянна по поверхности, но изменяется во времени (растет). Таким образом, температурный напор также не изменяется по поверхности, но зависит от времени.
Температура греющей среды – слегка перегретого, сухого насыщенного или влажного пара постоянна как по поверхности змеевика, так и во времени и представляет собой температуру насыщения ts, определяемую давлением пара. Температура раствора t постоянна по поверхности, но изменяется во времени (растет). Таким образом, температурный напор также не изменяется по поверхности, но зависит от времени.
Запишем уравнение теплового баланса теплообменника в дифференциальной форме
dQ* = (Mc)Sdt = k(ts -t)Fdt, (25)
где обозначено
(Mc)S = Mжcж+Mкcк+Mмcм+Mизcиз/2 (26)
Mмcм = Мм(cс+ Wсж)/(1+W) (27)
Потерями теплоты в окружающую среду при этом пренебрегаем ввиду их малости. Уравнение (25) учитывает равенство теплоты, затраченной на нагрев системы теплоте переданной через стенку змеевика за счет теплопередачи. Интегрирование уравнения (25) по времени позволяет получить
(Mc)S(tк -tн) = k(ts - átñ)Ft, (28)
где tк и tн – конечное и начальное значения температуры раствора.
После определения средней по времени температуры раствора átñ и вычисления коэффициента теплопередачи k это уравнение позволит найти величину площади поверхности змеевика F. Для решения первой задачи найдем закон изменения температуры раствора во времени. Проинтегрировав уравнение (25) методом разделения переменных после операции потенцирования получим
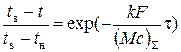 . (29)
. (29)
Среднее по времени значение определяется как среднеинтегральное, что позволяет записать
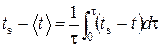 . (30)
. (30)
Вычисляя интеграл в (30) после подстановки в него функции (29) и исключая из полученного результата экспоненту с помощью того же выражения (29), получим
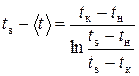 (31)
(31)
Значение коэффициента теплопередачи для змеевика записывается с учетом термического сопротивления загрязнений Rзаг
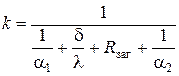 (32)
(32)
Коэффициент теплоотдачи со стороны конденсирующегося пара a1 существенно меньше, чем коэффициент теплоотдачи в жидкости a2 при свободной конвекции (a1>>a2). К тому же термическое сопротивление теплопроводности металлической стенки змеевика пренебрежимо мало. Это позволяет записать приближенное упрощенное уравнение для расчета k в виде
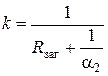 (33)
(33)
Средняя температура жидкости átñ уже известна, а температуру стенки tc, необходимую для вычисления коэффициента теплоотдачи a2 при свободной конвекции в итерационной процедуре можно воспользоваться уравнением, определяющем равенство плотностей потоков теплоты за счет теплоотдачи и через загрязнения
(ts - tc)/Rзаг =a2(tc - átñ )
Необходимым для расчета a2 значением диаметра трубы змеевика d задаемся в интервале 20 ¸ 30 мм. Сходимость итераций можно проверять по величине коэффициента теплоотдачи.
По найденной площади поверхности F рассчитывается длина l и число витков n змеевика согласно формулам
F = pdl l = npdзм
Диаметр змеевика dзм принимается меньшим внутреннего диаметра бака на величину (2 ¸ 3)d.
4. Установившийся режим крашения
В этом режиме затраты теплоты обусловлены лишь потерями в окружающую среду. Порядок расчета этой статьи теплового баланса остается прежним, с учетом того, что в качестве температуры жидкости используется температура, до которой был разогрет раствор. Поскольку в этом режиме система обогревается глухим паром, его масса определяется по тому же уравнению, что и разделе 3. Расход пара рассчитывается также как и ранее по массе пара и продолжительности процесса.
5. Расхолаживание красильного бака водой
Вода для расхолаживания подается в змеевик, площадь поверхности которого рассчитана в предыдущем разделе. И здесь ставится задача расчета расхода воды.
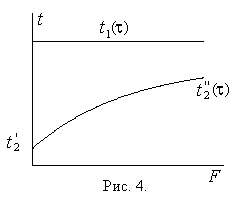 На рис. 4 представлен температурный график змеевикового теплообменника при расхолаживании. Температура t1 горячего теплоносителя (раствора) остается постоянной по поверхности, но изменяется во времени (уменьшается). Температура холодного теплоносителя на входе в теплообменник t2¢ поддерживается постоянной, а на выходе из него t2² изменяется во времени.
На рис. 4 представлен температурный график змеевикового теплообменника при расхолаживании. Температура t1 горячего теплоносителя (раствора) остается постоянной по поверхности, но изменяется во времени (уменьшается). Температура холодного теплоносителя на входе в теплообменник t2¢ поддерживается постоянной, а на выходе из него t2² изменяется во времени.
Дифференциальная форма уравнения теплового баланса имеет вид
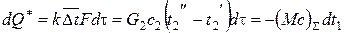 (34)
(34)
где 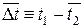 - среднее по поверхности теплообмена значение температурного напора в произвольный момент времени. Здесь и далее горизонтальная черта сверху будет использоваться для характеристики средних по поверхности величин.
- среднее по поверхности теплообмена значение температурного напора в произвольный момент времени. Здесь и далее горизонтальная черта сверху будет использоваться для характеристики средних по поверхности величин.
Второй член уравнения (34) характеризует теплоту, перенесенную за счет теплопередачи, третий – теплоту, полученную охлаждающей водой, и четвертый – теплоту, отданную раствором. Величина (Mc)S определяется теми же выражениями (26), (27), что и ранее.
Интегральная форма уравнения теплового баланса для всего периода расхолаживания будет иметь вид
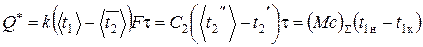 (35)
(35)
где C2 = G2c2 – расходная теплоемкость холодного теплоносителя.
Количество теплоты, передаваемой в процессе расхолаживания, рассчитывается по последнему члену в уравнении (35). Для нахождения расхода охлаждающей воды необходимо найти величину át2²ñ. Вычислим вначале среднее по поверхности значение температурного напора для любого момента времени. В соответствии с графиком рис. 4 больший температурный напор равен t1 - t2¢, а меньший t1 - t2², и искомое значение среднего по поверхности температурного напора, равное его среднелогарифмическому значению записывается как
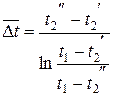 (36)
(36)
Подставляя полученное значение в уравнение, характеризующееся вторым знаком равенства в формуле (34), после простых преобразований получим
t2² - t2¢ = (t1 - t2¢)(1-exp(-N2)), (37)
где через N2 обозначено число единиц переноса
N2 = kF/C2. (38)
В уравнении (37) все члены, кроме t2² и t1, не зависят от времени. Поэтому результат его осреднения по времени можно представить как
át2²ñ - t2¢ = (át1ñ - t2¢)[1-exp(-N2)]. (39)
Для нахождения величины át1ñ, входящей в формулу (39) воспользуемся дифференциальным уравнением, определяемым последним равенством в (34), предварительно заменив в нем t2² - t2¢ при помощи формулы (37). Интегрирование полученного дифференциального уравнения метолом разделения переменных и потенцирование полученного результата позволяют получить зависимость температуры раствора от времени
t1 - t2¢ = (t1н - t2¢)exp{-C2 [1-exp(-N2)]t} (40)
Проведем процедуру осреднения во времени температуры раствора, аналогично тому, как это было сделано в разделе 3. Из полученного результата с помощью уравнения (40) исключим величину C2 [1-exp(-N2)], то дает
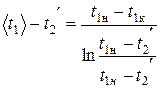 (41)
(41)
Подставим уравнение (39) в уравнение (35) со вторым знаком равенства и получим
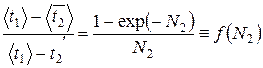 (42)
(42)
График функции f(N2), определяемый правой частью уравнения (42), показан на рис. 5. Чтобы найти величину С2 по формуле (38), по графику рис. 5 следует определить значение N2. Но для этого необходимо предварительно значение температуры 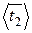 и величину коэффициента теплопередачи . Эта задача решается в процессе итераций следующим образом. Предварительно по известному количеству теплоты, площади и времени вычисляется средняя плотность теплового потока
и величину коэффициента теплопередачи . Эта задача решается в процессе итераций следующим образом. Предварительно по известному количеству теплоты, площади и времени вычисляется средняя плотность теплового потока
áqñ = Q*/(Ft)
Далее реализуется итерационная цепочка
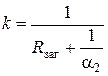 (43)
(43)
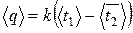 (44)
(44)
áqñ = (át1ñ - tc)/Rзаг (45)
Для реализации этой цепочки можно использовать следующую последовательность вычислений. Задаются значением коэффициента теплоотдачи a2 по порядку величины. Вычисляют коэффициент теплопередачи по формуле (43), из уравнения (44) находят 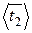 - среднюю по поверхности и времени темпера
- среднюю по поверхности и времени темпера 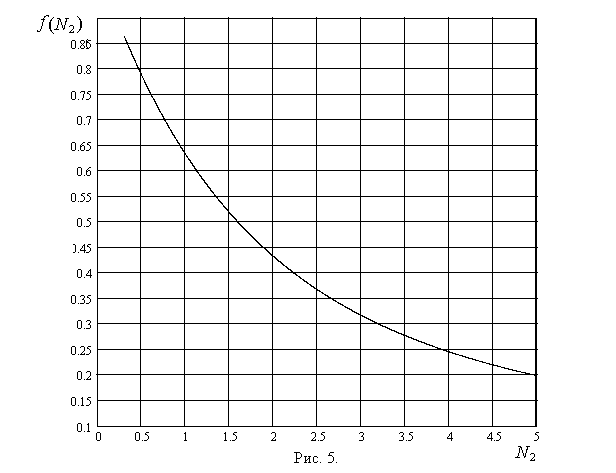 туру охлаждающей воды, а по формуле (45) среднюю по времени и поверхности температуру стенки tс. Эти две последние температуры используются при вычислении коэффициента теплоотдачи a2 по уравнению подобия для свободной конвекции, что позволяет найти уточненное значение коэффициента теплопередачи и т.д. Сходимость итераций проверяется по величине коэффициента теплопередачи k.
туру охлаждающей воды, а по формуле (45) среднюю по времени и поверхности температуру стенки tс. Эти две последние температуры используются при вычислении коэффициента теплоотдачи a2 по уравнению подобия для свободной конвекции, что позволяет найти уточненное значение коэффициента теплопередачи и т.д. Сходимость итераций проверяется по величине коэффициента теплопередачи k.
После того, как найдена в процессе итераций температура 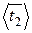 , левая часть уравнения (42) легко рассчитывается и тем самым определяется функция f(N2), по величине которой при помощи графика рис. 5 определяется величина N2. Далее по найденному значению коэффициента теплопередачи по уравнению (38) рассчитывают величину С2, а по ней – расход воды.
, левая часть уравнения (42) легко рассчитывается и тем самым определяется функция f(N2), по величине которой при помощи графика рис. 5 определяется величина N2. Далее по найденному значению коэффициента теплопередачи по уравнению (38) рассчитывают величину С2, а по ней – расход воды.
При необходимости получения более точных результатов следует численно решать нелинейное уравнение (42) относительно N2.
Представление результатов расчета
Для каждого из процессов, рассчитанных в разделах 1 - 4, составить таблицы, включающие затраты теплоты по отдельным составляющим и рассчитать их долю. Найти суммарные затраты теплоты на весь процесс обработки материала и найти удельные, отнесенные к 1кг материала. Найти суммарные затраты пара, а также удельные, отнесенные к 1кг материала.
Приложения
Плотность и теплоемкость сталей
| металлы и сплавы | Т, К | r×10-3, кг/м3 | с, кДж/(кг ×К) |
| Стали: |
7,8
| ||
| высоколегированные | 300 | 0,48-0,50 | |
| 800 | 0,55-0,60 | ||
| низко- и средне-легированные | 300 | 0,46 | |
| легированные | 800 | 0,50—0,55 | |
| стальное литье | 300 | 0,46 | |
| » » | 800 | 0,57 | |
| углеродистые | 300 | 0,46 | |
| » » | 400 | 0,50 | |
| » » | 600 | 0,52—0,58 | |
| » » | 800 | 0,66—0,69 |
Плотность текстильных материалов
| Волокно | Плотность r×10-3, кг/м3 | Волокно | Плотность r×10-3, кг/м3 |
| Хлопок | 1,5...1,55 | Медно-аммиачное | 1,52 |
| Шелк обесклеенный | 1,35 | Ацетатное | 1,33 |
| шерсть | 1,304...1,32 | Льняное | 1,5 |
| Вискозное | 1,52...1,534 | Нейлоновое | 1,14 |
Теплоемкость текстильных материалов
| Материал | cс, кДж/(кг×К) | Материал | cс, кДж/(кг×К) |
| Хлопок | 1,33 | Шелк | 1,38 |
| Лен | 1,35 | Нейлон | 1,43 |
| Шерсть | 1,36 | Вискозное волокно | 1,36 |
Характеристики теплоизоляционных материалов
| Наименование | r, кг/м3 | l, Вт/мК | СР, КДж/кгК | 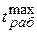 , оС , оС
|
| Картон асбестовый толщиной 2-10 мм | 1000-1300 | 0,157+14.10-5 t | 0,84 | 500 |
| Ткань асбестовая АСТ со стеклонитью | 600 | 0,124+18.10-5 t | 0,86 | 450 |
| Шнур асбестовый ШАОН диаметром 10-55 мм | 550-750 | 0,14+23.10-5 t | 0,85 | 400 |
| Асбестовермикулитовые плиты | 300 | 0,095+23,3.10-5 t | 0,84 | 600 |
| Маты из штапельного стекловолокна в рулоне | 55 | 0,04+41.10-5 t | 0,84 | 500 |
| Вата минеральная в набивке (марка 100) | 150 | 0,046+23.10-5 t | 0,92 | 600 |
| Маты прошивные из минеральной ваты ВФ-75 | 150-200 | 0,049+20.10-5 t | 0,92 | 600 |
| Плиты минераловатные на синтетическом связующем | 115 | 0,043+22,1.10-5 t | 0,92 | 400 |
| Войлок технический | 170 | 0,047+19,8.10-5 t | 1,88 | 70 |
| Полистирольные пенопластовые плиты | 25-40 | 0,052 | - | 70 |
| Полиуретановые пенопластовые плиты | 50-60 | 0,032 | - | 100 |
Литература
1. Теплоиспользующие установки в текстильной промышленности / под ред. Е.А.Ганина, М., Легпромбытиздат, 1989.
2. А.М.Бакластов, В.А.Горбенко, П.Г.Удыма, Проектирование, монтаж и эксплуатация тепломассообменных установок, М., Энергоиздат, 1981.
3. Промышленные тепломассообменные процессы и установки / под ред. А.М.Бакластова, М., Энергоатомиздат, 1986.
4. И.П.Корнюхин, Тепломассообмен в теплотехнике текстильного производства, М., Изд. МГТУ, 2004.
5. С.Л.Ривкин, А.А.Александров, Термодинамические свойства воды и водяного пара (справочник), М., Энергоатомиздат, 1984.
Содержание
Стр
Технологии обработки текстильных материалов в жидкости…………………..3
Теплотехнический расчет красильной машины периодического действия……5
1. Стадия подогрева раствора красителя в приготовительном баке…………6
2. Установившийся режим работы приготовительного бака………………...11
3. Разогрев красильного бака глухим паром……………………………………..11
4. Установившийся режим крашения……………………………………………15
5. Расхолаживание красильного бака водой……………………………………..15
Представление результатов расчета……………………………………………...18
Приложения………………………………………………………………………..18
Список литературы………………………………………………………………..20








