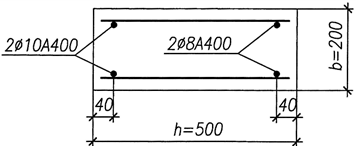
Рис. 7. Схема расположения сечений и эпюры усилий в балке
Расчет элементов нижнего пояса балки. Сечение 12, нормальное к про- дольной оси элемента (рис. 8, а) N = 986,0 кН, М = 22,02 кН·м
.
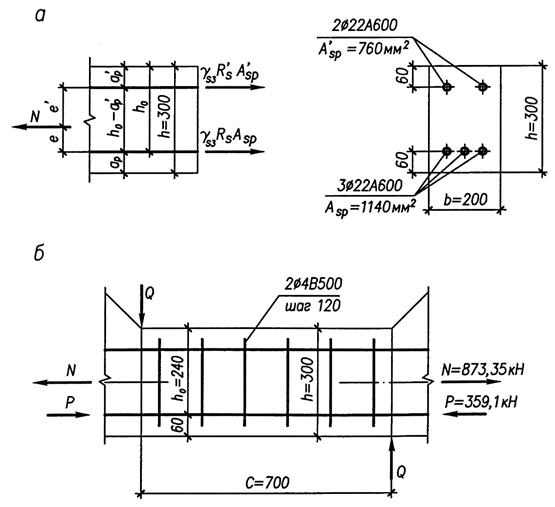
Рис. 8. К расчету прочности сечений нижнего пояса балки: а – для определения площади продольной арматуры; б – к проверке прочности по наклонным сечениям
Расчет прочности выполняем согласно п. 3.70[7] c уточнением для предва- рительно напряженного элемента. Вычисляем эксцентриситет продольной силы е0 = М / N = 22,02 / 986,0 = 0,0223 м = 22,3 мм. Эксцентриситеты арматур S p и S ' р соответственно равны:
е' = е0 + h / 2 − а' р = 22,3 + 300 / 2 − 60 = 112,3 мм;
е = − е0 + h / 2 − а р = −22,3 + 300 / 2 − 60 = 67,7 мм.
Так как е’ = 112,3 мм < h0 − а' р = 240 − 60 = 180 мм, то продольная сила приложена между равнодействующими усилий в арматуре S p и S ' р и требуемые площади арматур вычисляем по формулам (3.138) и (3.139) [7]:
A sp = Ne ' /[γ s3 R s(h0 − а' р)] = 986,0·103·112,3/[1,1·520(240 − 60)] = 1075 мм2;
где γ s3= 1,1 (см. п. 3.9 [9]).
Принимаем 3Ø22A600, A sp , fact = 1140 мм2.
A ' sp = Ne/[γ s3R s(h0−а' р)] = 986,0·103·67,7/[1,1·520(240 − 60)] = 648 мм2;
Принимаем 2Ø22A600, A sp , fact = 760 мм2.
Выполняем расчет прочности наклонного сечения нижнего пояса балки в наиболее загруженном элементе между расчетными сечениями 9 и 10 (см. рис.
3.7 и 3.8, б) в соответствии с п. 3,34 [9] c учетом указаний п. 3.71 [7] на дейст- вие поперечной силы Q = 28,4 кН.
Расчет выполняем с учетом наличия продольной растягивающей силы N =
=873,35 кН и усилия обжатия от напрягаемой арматуры, расположенной в наи- более растянутой зоне Р = σsp2A sp=350 ·1140=399000 Н =399,0 кН , где σsp2 =
=0,7σsp = 0,7·500 = 350 МПа, (коэффициент 0,7 учитывает, что полные потери
предварительного напряжения приблизительно будут равны 0,3σ sp).
Примем поперечное армирование по конструктивным соображениям в ви- де замкнутых двухветвевых хомутов из арматуры диаметром 4 мм класса В500 с максимальным конструктивным шагом s w = h0/2 =240/2 =120 мм (A sw =2·12,6=
= 25,2 мм2, R sw = 300 МПа).
Определим коэффициент φ nt по формуле (3.143) [7], принимая:
А= bh = 200 · 300 = 60000 мм2:
φ nt
= 1 +
N - P
1,5R bt A
= 1 + 873350 - 399000 = 4,765.
1,5 ×1,4 × 60000
Вычисляем величины M b и q sw :
M b = 1,5 R bt b h2 / φ
= 1,5·1,4·200·2402 / 4,765 = 5,007·106 Н·мм;
0 nt
q sw = R sw A sw / s w = 300·25,2/120 = 63,0 Н / мм.
Поскольку q sw > 0,25R bt b / φ nt = 0,25 ·1,4·200/4,765=14,69 Н / мм, то M b не корректируем.
Находим Q b , min = 0,5R bt bh0/φ nt = 0,5·1,4·200·240/4,765 =7051 H = =7,05 кН.
Так как поперечная сила не изменяется по длине элемента, принимаем длину проекции наклонного сечения равной длине элемента с =700 мм < 3h0=
= 3·240 = 720 мм. Тогда с0 = с = 700 мм > 2h0 = 2·240 = 480 мм, т.е с0 = 480 мм.
Находим Q b = M b / с = 5,007·106 / 700=7153 Н = 7,15 кН > Q b , min = 7,05 кН;
Q sw = 0,75 q sw с0 = 0,75·63,0·0.48 = 22,68 кН.
Таким образом, предельная несущая способность нижнего пояса балки в наиболее опасном наклонном сечении будет равна:
Q = Q b + Q sw= 7,15 + 22,68 = 29,83 кН > Q = 28,4 кН,
следовательно, прочность нижнего пояса балки на действие поперечной силы обеспечена. Требования п. 3.36[9] также выполняются, поскольку:
s w,max =
R bt bh02 / Q =
1,4·200·2402
/ (28,4·103) = 567 мм > s w= 120 мм.
Расчет элементов верхнего пояса балки. Сечение 4, нормальное к про- дольной оси элемента (рис. 9, а), N = 992,37 кН, М = 48,65 кН·м.
Расчетная длина в плоскости балки, согласно таблице IV.10 приложения IV, будет равна l0 = 0,9·1,5=1,35 м. Так как l0 / h = 1350 / 420 = 3,21 < 4, то расчет ведем без учета прогиба элемента.
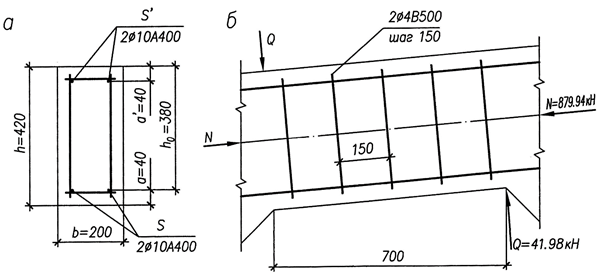
Рис. 9. К расчету прочности сечений верхнего пояса балки:
а – для определения площади продольной арматуры;
б – к проверке прочности по наклонным сечениям
Находим e0 = M /N = 48,65/992,37 = 0,049 м = 49 мм. Поскольку случайный эксцентриситет е а = h / 30 = 420 / 30 = 14 мм < е0= 49 мм, то оставляем для рас- чета е0 = 49 мм. Тогда эксцентриситет продольного усилия относительно арма- туры S будет равен е = е а + ( h0 − а') / 2 =49 + (380 − 40) / 2 = 219 мм.
Требуемую площадь сечения продольной рабочей арматуры класса А400 (R s = R sc = 350 МПа, ξ R = 0,533 и α R = 0,391) определим согласно п. 3.60 [7] по формулам (3.102) и (3.103):
N e - α R bh2

|
A' = R b 0
992,37 × 10 3 × 219 - 0,391 × 22 × 200 × 3802
=
= -261 мм2 < 0;
R sc
(h0
- a' )
350(380 - 40)

|
|
|
A = ξ R R b bh0 - N + '
R s
= 0,533 × 22 × 200 × 380 - 992,37 × 10
|
350
+ 0 = -289 мм2 < 0.
Принимаем в сжатой и растянутой зонах конструктивное армирование по
2Ø10А400,
A  = A
= A  ' = 157 мм2 > μ min= 0,001bh0=0,001·200·380=76 мм2.
' = 157 мм2 > μ min= 0,001bh0=0,001·200·380=76 мм2.
| |
| |
Элемент 1 – 2, сечение, наклонное к продольной оси (рис. 9, б), Q = 41,98 кН, N = 879,94 кН.
Расчет выполняем согласно пп. 3.41 и 3.52 [7]. Находим коэффициент φ n2
по формуле (3.84) [7]:
|
2
N æ N ö æ ö

|
φ = 1+ 3
- 4ç ÷
= 1+ 3 879,94 - 4ç 879,94 ÷
= 1+1,099 - 0,5366 = 1,562,

|
n 2
b
ç ÷
è b ø

2402,4

è 2402,4 ø
где N b =1,3R bA=1,3·22·200·420=2402,4·103 Н =2402,4 кН > N=878,94 кН.
Проверим условие (3.64) [7]:
2,5R btbh0 = 2,5·1,4·200·380 = 266·103 Н = 266 кН >Q = 41,98 кН,
т. е. условие выполняется.
Проверим условие (3.65) [7], принимая максимальное конструктивное значение с = 700 мм:
|
1,5φ R b h2 /c =1,5·1,562·1,4·200·3802
/ 700 =
=135,3 ·103 Н=135,3 кН > Q= 41,98 кН,
т. е. и второе условие выполняется. Следовательно, прочность наклонного сечения обеспечена без поперечной арматуры.
С учетом конструктивных требований для сжатых элементов принимаем поперечную арматуру для верхнего пояса балки диаметром 4 мм класса В500 с шагом, равным 15d = 15 ·10 = 150 мм.
Расчет стоек балки. Стойки решетчатой балки рассчитываются на небла- гоприятные сочетания усилий N и М без учета длительности действия нагрузок, так как всегда l0 / h < 4. Для примера рассмотрим порядок определения площади сечения продольной арматуры в сжато-изогнутой стойке 17 −18 (рис. 10), N =
=2,21 кН, М = 18,70 кН·м, −М = −8,89 кН·м.