Расчетно-графическое задание
 Министерство науки и высшего образования Российской Федерации
Министерство науки и высшего образования Российской Федерации
Федеральное государственное образовательное учреждение высшего образования
НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ АРХИТЕКТУРНО-СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ(Сибстрин)
ИНСТИТУТ ДОПОЛНИТЕЛЬНОГО ОБРАЗОВАНИЯ
Расчетно-графическое задание
Тема: «Многопролетная статическая определимая балка»
Схема 22
| Выполнил: ___________ Ибрагимов Д.И подпись фамилия и инициалы ________________ дата | Проверил: ___________ Вешкин М.С. подпись фамилия и инициалы ________________ дата |
Новосибирск 2025
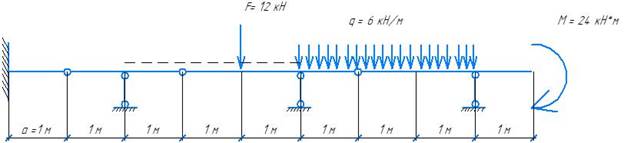
Дано: a = 1 м, F = 12кН, q = 6 кН/м, M = 24 кН*м, p = 4 кН/м
F, q, M - компоненты постоянной нагрузки;
p - временная нагрузка.
СОДЕРЖАНИЕ РАСЧЕТНОГО ЗАДАНИЯ
1. Выполнить кинематический анализ исходной расчётной схемы МСОБ. Составить рабочую схему балки.
2. Поэлементным расчётом определить опорные реакции, изгибающие моменты и поперечные силы от заданной постоянной нагрузки. Выполнить статическую проверку полученных результатов. Построить эпюры Mconst и Qconst .
3. На участке, отмеченном штриховой линией, построить объемлющую эпюру изгибающих моментов, учитывая постоянную нагрузку и временную – распределённую p, прикладываемую попролётно).
Указание: расчётные сечения назначить с шагом a /2.
1 Кинематический анализ
1.1 Количественный анализ (Предварительный)
W = 3D – 2H – C0
D – число дисков, Н – число простых шарниров, C0 – число связей с землей.
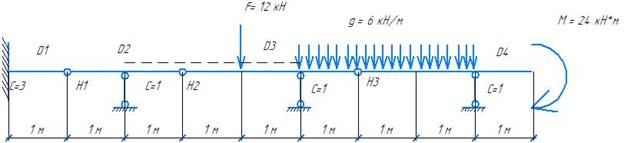
Расчетная схема
W = 3*4 – 2*3 – 6 = 0 - связей достаточно для определение ГНС. Система может быть СОС, если ГНС
1.2 Структурный анализ
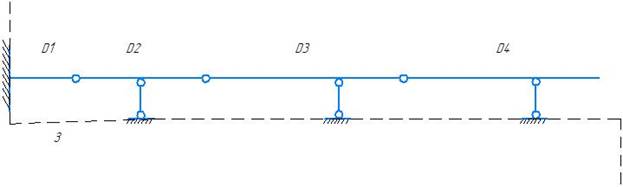
- Земля и диск D1 образуют ГНС ( заделка ) и образуют НЗ1.
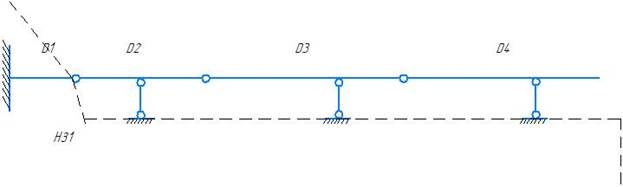
- НЗ1 с диском D2 образуют ГНС (связи: простой шарнир, линейная связь.) ось линейной связи не проходит через центр простого шарнира. Образуют НЗ2.
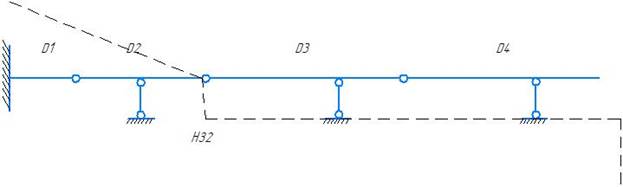 - НЗ2 с диском D3 образуют ГНС (связи: простой шарнир, линейная связь.) ось линейной связи не проходит через центр простого шарнира. Образуют НЗ3.
- НЗ2 с диском D3 образуют ГНС (связи: простой шарнир, линейная связь.) ось линейной связи не проходит через центр простого шарнира. Образуют НЗ3.
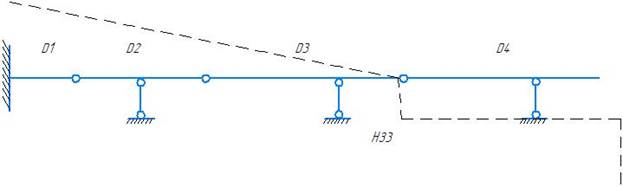 - НЗ3 с диском D4 образуют ГНС (связи: простой шарнир, линейная связь.) ось линейной связи не проходит через центр простого шарнира. Образуют НЗ4.
- НЗ3 с диском D4 образуют ГНС (связи: простой шарнир, линейная связь.) ось линейной связи не проходит через центр простого шарнира. Образуют НЗ4.
Многопролетная балка является ГНС, а значит СОС (статически определимой системой).
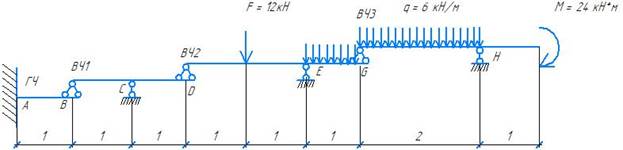
Рабочая схема балки
2) Определение опорных реакций
- Второстепенная часть 3
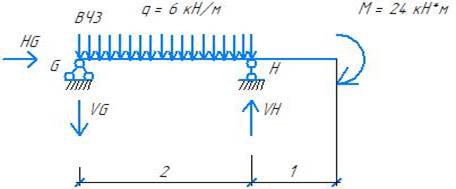
∑mG = 0
q*2*1 + M – VH*2 = 0
VH = (M + 2q)/2 = (24+6*2)/2 = 36/2 = 18 kH
∑mH = 0
-q*2*1 + M – VG*2 = 0
VG = (M – 2q)/2 = (24 – 6*2) = 12/2 = 6 kH
∑Fx = 0
HG = 0
Проверка
∑Fy = 0
-q*2 + 18 – 6 = - 12 + 18 – 6 = 0
0=0
- Второстепенная часть 2
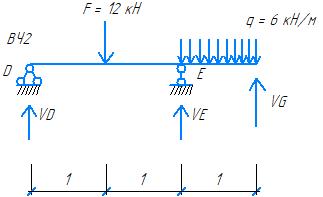
∑mE= 0
q*1*0.5 + VD*2 –F*1 – VG*1 = 0
VD = (F - q/2 + VG)/2 = (12 – 3 + 6)/2 = 15/2 = 7.5 kH
∑mD = 0
q*2.5 + F – VE*2 – VG*3 = 0
VE = (F + 2.5q – VG*3)/2 = (12 + 6*2.5– 6*3) = 9/2 = 4.5 kH
Проверка
∑Fy = 0
- q*1 – F + VG + VE + VD = 0
- 12 - 6 + 6 + 7.5 + 4.5 = 0
0=0
- Второстепенная часть 1
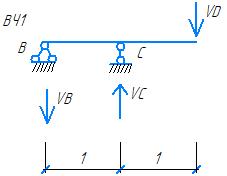
∑mC= 0
-VB + VD = 0
VB = VD = 7.5 kH
∑mB= 0
-VC + VD*2 = 0
VC = VD*2 = 15 kH
Проверка
∑Fy = 0
-7.5 + 15 – 7.5 = 0
0=0
- Главная часть
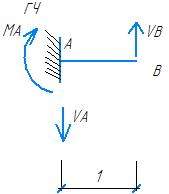
∑mA= 0
-VB + M = 0
M = VB = 7.5 kH
∑mB= 0
M - VA = 0
VA = M = 7.5 kH
Проверка
∑Fy = 0
-7.5 + 7.5 = 0
0=0
Эпюра моментов и поперечных сил
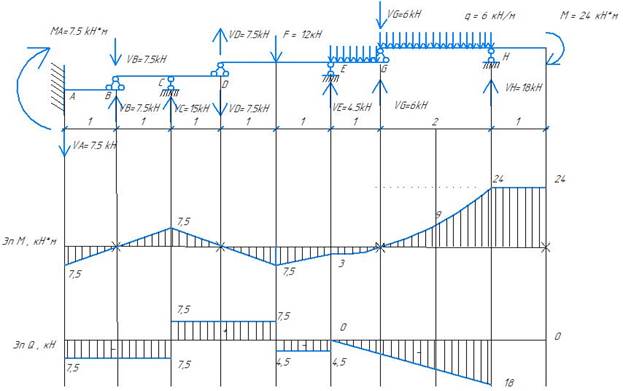
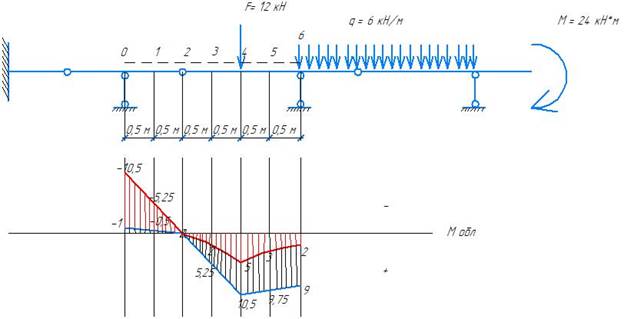
3. Построение объемлющей эпюры
Эпюра временной нагрузки 1
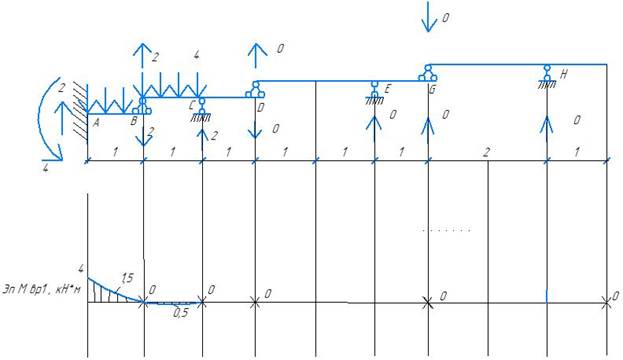
Эпюра временной нагрузки 2
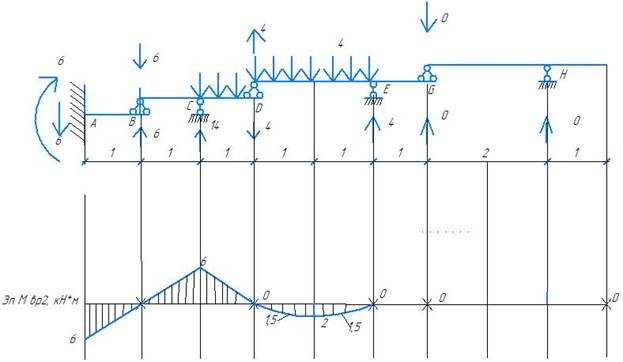
Эпюра временной нагрузки 3
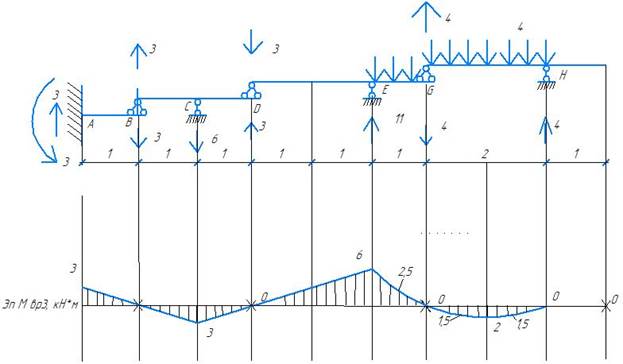
Эпюра временной нагрузки 4
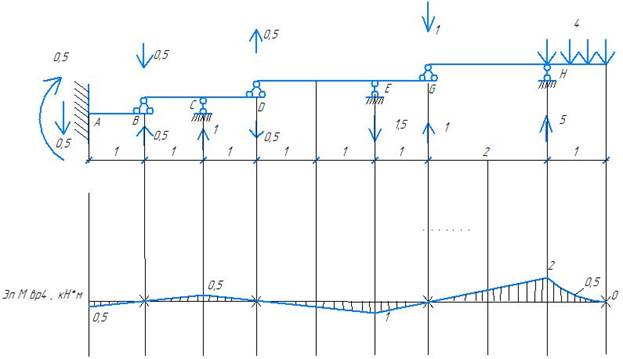
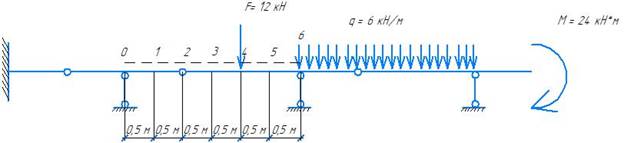
Таблица расчетных сочетаний усилий (РСУ)
Мрас (маx) = М пост + ∑ М врi (>0)
Мрас (мin) = М пост + ∑ М врi (<0)
| № | М пост | М вр1 | М вр2 | М вр3 | М вр4 | М расч | кН*м | |
| max | min | |||||||
| 0 | -7,5 | 0 | 6 | -3 | 0,5 | -1 | -10,5 | |
| 1 | -3,75 | 0 | 3 | -1,5 | 0,25 | - 0,5 | - 5,25 | |
| 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 3 | 3,75 | 0 | -1,5 | 1,5 | - 0,25 | 5,25 | 2 | |
| 4 | 7,5 | 0 | -2 | 3 | - 0,5 | 10,5 | 5 | |
| 5 | 5,25 | 0 | -1,5 | 4,5 | - 0,75 | 9,75 | 3 | |
| 6 | 3 | 0 | 0 | 6 | - 1 | 9 | 2 | |








