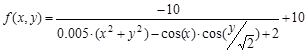Задание 1 Найти экстремум целевой функции y ( x ).
Варианты заданий по теме «Генетические алгоритмы»
Задание 1 Найти экстремум целевой функции y ( x ).
Размер популяции – 50 особей
Длина хромосомы - 20 бит
Область поиска - [ - 5 ; 5 ]
| N вар иан та | Целевая функция | Искомый экстре мум | Способ кодирования хромосом | Вероятности | Генетические операторы | ||
| скрещи вания Pc | мута ции Pm | формирование родительских пар | редукция | ||||
| 1 | Y=2*x-3.3*x.*cos(9.3*x)-2.3*sin(1.7*x) | min | двоичный код | 0,9 | 0,2 | турнир | |
| 2 | y=exp(-0.5*x.^2).*sign(cos(9.3*x-1)) | min | код Грея | 0,9 | 0,1 | случайный отбор | рулетка |
| 3 | y=-0.6*x+5.3*abs(cos(6.1*x)).*cos(3.6*x) | min | двоичный код | 0,8 | 0,2 | случайный отбор | турнир |
| 4 | y=-1.3*sin(1.6*x.^2-0.3).*exp(-0.3*x+0.5) | max | код Грея | 0,85 | 0,15 | лучшие с лучшими | рулетка |
| 5 | y=0.9*abs(sin(3.7*x)).*cos(6.1*x) | max | двоичный код | 0,9 | 0,15 | случайный отбор | турнир |
| 6 | y=0.8*x+1.4*cos(1.8*x.^2).*exp(0.4*x) | min | код Грея | 0,85 | 0,1 | лучшие с лучшими | рулетка |
| 7 | y=-sin(0.9*x-1)- sin(1.8*x-1).*cos(7.8*x) | max | двоичный код | 0,8 | 0,15 | лучшие с лучшими | турнир |
| 8 | y=0.8*x+1.1*x.*sin(9.3*x)-0.7*cos(0.8*x) | min | код Грея | 0,9 | 0,1 | случайный отбор | рулетка |
| 9 | y=0.2*x-1.1*exp(-0.4*x.^2).*sign(cos(9.5*x+1.5)) | min | двоичный код | 0,85 | 0,15 | лучшие с лучшими | турнир |
| 10 | y=0.3*x+x.*cos(7.3*x)-0.7*sin(1.3*x) | max | код Грея | 0,8 | 0,2 | случайный отбор | рулетка |
| 11 | y=exp(-0.8*x).*sign(sin(9.3*x)) | max | двоичный код | 0,85 | 0,15 | случайный отбор | турнир |
| 12 | y=0.4*sin(0.8*x+0.9)+ 0.7*cos(0.8*x-1).*sin(7.3*x) | min | код Грея | 0,8 | 0,2 | лучшие с лучшими | рулетка |
| 13 | y=-0.6*x+4.2*sin(1.5*x.^2+0.7)+0.2*(x.^2+1.4) | min | двоичный код | 0,9 | 0,1 | случайный отбор | турнир |
| 14 | Y=1.5*x+3.5*cos(2.1*x.^2+3)-0.5*(x.^2) | max | код Грея | 0,85 | 0,15 | случайный отбор | рулетка |
| 15 | Y=0.1*x-1.7*abs(sin(5.8*x)).*cos(3.2*x) | min | двоичный код | 0,8 | 0,15 | случайный отбор | турнир |
* - умножение
Способ мутации:
- при кодировании хромосомы двоичным кодом – точечная мутация.
- при кодировании хромосомы кодом Грея – инверсия
Содержание отчета:
1. График целевой функции y(x) в пределах области поиска.
2. Функция, используемая для определения приспособленности особей.
3. 3 популяции особей:
- начальная (нулевая)
- вторая
- последняя
для каждой особи указать значение х, закодированное значение х – хромосому, значение целевой функции у(х) и приспособленность f(x);
| Номер особи в популяции | x | хромосома | y(x) | f(x) |
| … | … | … | … | … |
вычислить среднюю приспособленность особей в каждой популяции.
4. Фрагменты программного кода, реализующие генетические операторы:
- генерация начальной популяции
- формирование родительских пар
- скрещивание
- точечная мутация
- редукция
Задание 2:
Найти экстремум функции двух переменных f( x, y).
- Примеры функций (на выбор):
1. 
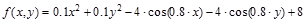(ф-я Растригина)
2. 
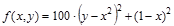(функция Розенброка)
