II. Систематизация и обобщение ранее изученного.
Тема урока: Решение задач по теме «Многогранники».
Цели урока:
Образовательная:
Ø систематизировать и обобщить знания учащихся по теме «Многогранники» и обеспечить их применение при решении задач вариантов ЕГЭ;
Ø способствовать развитию пространственного воображения и графической грамотности.
Ход урока.
I. Организационный момент (время- 3').
- Эпиграф урока: «Никакое дело нельзя хорошо сделать, если неизвестно, чего хотят достигнуть» (Антон Семенович Макаренко)
Решите кроссворд.
По горизонтали:
1)Элемент многогранника.
2)Перпендикуляр, опущенный из вершины пирамиды на основание.
3)Призма, у которой боковое ребро перпендикулярно к основанию.
4)Многогранник, две грани которого являются равными многоугольниками, лежащими в параллельных плоскостях, а остальные грани —параллелограммами, имеющими общие стороны с этими многоугольниками.
5)Теорема, связывающая число граней, число вершин и число ребер выпуклого многогранника. (Автор теоремы).
6)Призма, основанием которой является параллелограмм.
7) Правильный многогранник, каждая грань которого представляет собой
квадрат.
По вертикали:
1.Правильный восьмигранник.
2. Поверхность, составленную из многоугольников и ограничивающую некоторое геометрическое тело
3.Высота боковой грани правильной пирамиды.
4. Многогранник, одна грань которого многоугольник, а остальные грани - треугольники с общей вершиной.
5. Элемент многогранника.
6. Прямая призма, в основание которой лежит правильный многоугольник.
7. Пирамида, у которой вершинами служат вершины основания и вершины ее сечения плоскостью, параллельной основанию.
| 1 | |||||||||||||||||||
| 3 | |||||||||||||||||||
| 2 | 4 | ||||||||||||||||||
| 1 | 5 | ||||||||||||||||||
| 3 | |||||||||||||||||||
| 2 | 7 | ||||||||||||||||||
| 5 | 6 | ||||||||||||||||||
| 4 | |||||||||||||||||||
| 7 | |||||||||||||||||||
2) Тест.
1 вариант.
а) Какую фигуру представляет боковая грань призмы?
1) квадрат; 2) параллелограмм; 3) прямоугольник.
б) Какую фигуру представляет боковая грань правильной пирамиды?
1) треугольник; 2) прямоугольный треугольник; 3) равнобедренный треугольник.
в) Какой многоугольник лежит в основании правильной 4-хугольной призмы?
1) квадрат; 2)параллелограмм; 3)прямоугольник.
г) Сколько диагоналей можно провести в 4-хугольной призме?
1) 2; 2) 4; 3) 6.
д) Сколько рёбер у шестиугольной призмы?
1) 18; 2) 6; 3) 24;
е) Измерениями прямоугольного параллелепипеда называются:
1) длины трёх произвольно взятых диагоналей;
2) длины трёх равных рёбер параллелепипеда;
3) длины трёх рёбер, имеющих общую вершину;
4) длины диагоналей основания параллелепипеда;
5) длины смежных сторон и диагонали параллелепипеда.
II вариант.
а) Какой многоугольник лежит в боковой грани параллелепипеда?
. 1) квадрат; 2) параллелограмм; 3) прямоугольник
б) Какую фигуру представляет основание правильной треугольной призмы?
1) равносторонний треугольник;
2) равнобедренный треугольник;
3) прямоугольный треугольник.
в) Какую фигуру представляет боковая грань прямой призмы?
1) квадрат; 2)параллелограмм; 3)прямоугольник.
г) Какую фигуру представляют сечения, проходящие через боковые ребра у прямой призмы?
1) квадрат; 2)параллелограмм; 3)прямоугольник.
д) Сколько граней у шестиугольной пирамиды?
1) 6; 2) 7; 3) 10; 4) 1
е) Апофема- это
1) высота боковой грани пирамиды;
2) высота пирамиды;
3) высота боковой грани правильной пирамиды.
3) Составление кластера по теме «Площади».
. Посередине листа в рамке написать слово «Площадь» и для данного перечня геометрических фигур выполнить следующие задания:
1. нарисовать саму фигуру;
2. написать формулу нахождения площади этой фигуры.
Геометрические фигуры: прямоугольный треугольник, равносторонний треугольник, любой треугольник, квадрат, прямоугольник, трапеция, круг, площади боковой и полной поверхностей для призмы и пирамиды.
II. Систематизация и обобщение ранее изученного.
1) решение задач ЕГЭ. Задачи:
№1. Найдите квадрат расстояния между вершинами D и C2многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
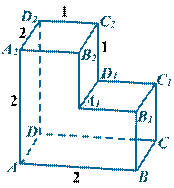
№2. Найдите угол C1BC прямоугольного параллелепипеда, для которого AB = 5 , AD = 4, AA1 = 4. Ответ дайте в градусах.
№1. Найдите расстояние между вершинами A и D1 прямоугольного параллелепипеда, для которого AB = 5, AD = 4, AA1 = 3.
№2.В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 1. Найдите уголAC1C. Ответ дайте в градусах.
№1.В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 1. Найдите расстояние между точками B и E.
№2. В правильной четырехугольной пирамиде SABCD точка O - центр основания, S -вершина,
SO = 4, SC = 5. Найдите длину отрезка AC.
2) Практическая работа.
I уровень. (Карточки зелёного цвета.)
Карточка №1.
Найти площадь поверхности данной фигуры.
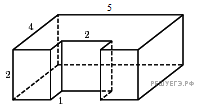
Карточка №2.
Если каждое ребро куба увеличить на 1, то его площадь поверхности увеличится на 54. Найдите ребро куба.
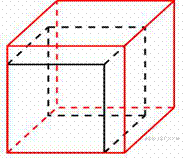
Карточка №3.
Во сколько раз увеличится площадь поверхности октаэдра, если все его ребра увеличить в 3 раза?
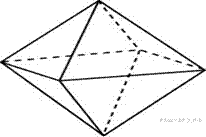
II уровень. (Карточки синего цвета.)
Карточка №1.
Основание прямого параллелепипеда - ромб. Найдите площадь боковой поверхности параллелепипеда, если площади его диагональных сечений Р и Q.
Карточка №2.
Диагональное сечение правильной четырехугольной призмы имеет площадь Q. Найдите площадь боковой поверхности призмы.
Карточка №3.
В прямой призме АВСА1В1С1 АВ = 13, ВС = 21, АС = 20. Диагональ боковой грани А1С составляет с плоскостью грани СС1В1В угол 30°. Найдите площадь полной поверхности призмы.
III уровень.(Карточки красного цвета).
Карточка №1.
Основание пирамиды - прямоугольный треугольник с катетом 4√3 см и противолежащим углом 60°. Все боковые ребра пирамиды наклонены к плоскости основания под углом 45°. Найдите площадь боковой поверхности пирамиды.
Карточка №2.
Основание пирамиды - прямоугольный треугольник с острым углом 30°. Высота пирамиды равна 4 см и образует со всеми боковыми ребрами углы 45°. Найдите площадь боковой поверхности пирамиды.
Карточка №3.
В правильной треугольной пирамиде сторона основания равна m. Угол между смежными боковыми гранями равен 120°. Найдите площадь боковой поверхности пирамиды.
V. Домашнее задание.
№1.Задача.
Сколько штук досок размером 100 мм на 2500 мм потребуется на обшивку крыши и потолка сарая, если длина крыши 4 м, ширина 3 м, а высота 2 м? Крыша имеет форму прямой треугольной призмы, в основании которой равнобедренный треугольник.








