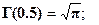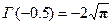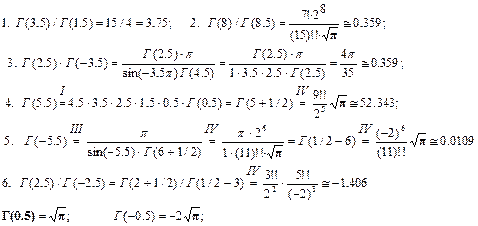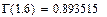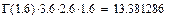Глава «Уравнение и функции Бесселя».
Методическая литература.
1. Ряды Фурье-Бесселя и их приложения: методические указания. А.С. Бондарев и др.;ЛЭТИ, СПб, 1992.
- Специальные функции: методические указания. А.С. Бондарев и др.;ЛЭТИ, СПб, 1993
3. Методы математической физики: учебное пособие. Ф.Л. Меркулов и др.СПбГЭТУ «ЛЭТИ», 2006.
§1 Гамма функция.
Известно понятие факториала для натурального числа:
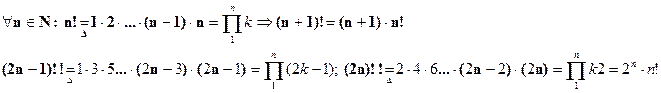
Определим на множестве R «гамма-функцию Г( x ) », которая на множестве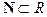 
определяет факториал натурального числа: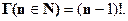 
Определение.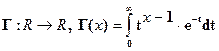 
Замечание. Функция Г(х) является сужением на R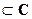 
комплексно-значной функции
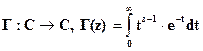
Следствия. Свойства гамма функции.
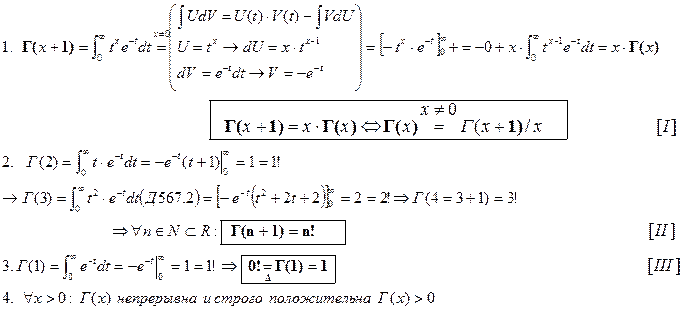
5. Утверждение.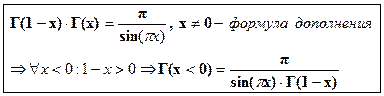 
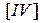
6. 
====================================================
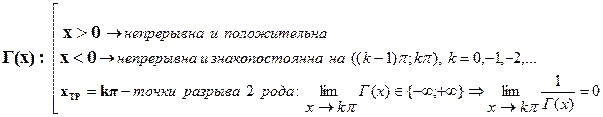
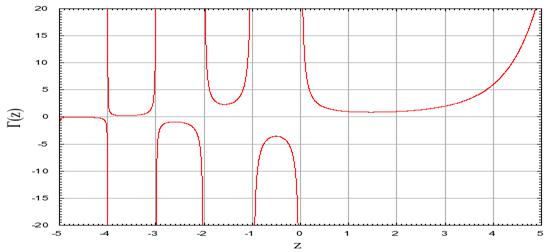
§2 Вычисление значений гамма функции.
1) 
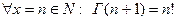
2) 
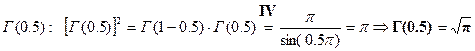
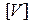
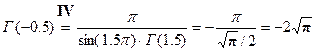
4)
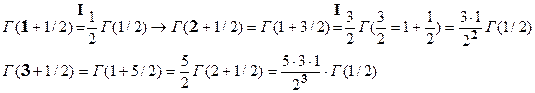
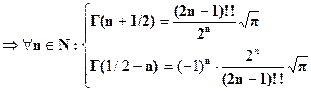
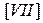
Свойства [I-VI] позволяют свести вычисление значений гамма-функции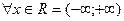 
к вычислению значений Г(х) на конечном промежутке.
5) Вычисление Г(х) через значения гамма-функции на (1;2).
5.1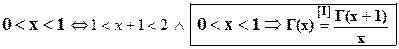 
5.2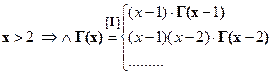 
è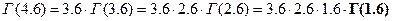 
(0.893∙10-3)
|
|
|
|
|
|
5.3 x < 0 :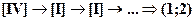 
è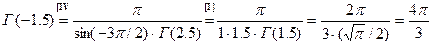 
Рекомендации по вычислениям значений гамма-функции.
(1) Вычисление Г(z) в MathCad.
Γ ( z ) возвращет значение гамма-функции в точке z .
(Для ввода оператора Г: введите G→[Ctrl]G )
(2 Для вычисления приближённых значений Г(1<x<2) можно использовать следующую аппроксимацию.
|
|
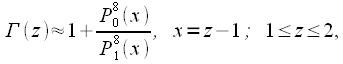
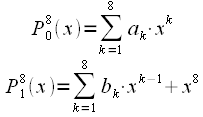
Коэффициенты полиномов аппроксимации подобраны так, чтобы обеспечивать наименьшую ошибку аппроксимации. Значения коэффициентов полиномов приведены в таблице:
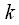
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
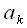
| 6.65e+4 | -3.61e+4 | -3.14e+4 | 866.97 | 629.33 | -379.8 | 24.77 | -1.716 |
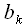
| -1.15e+5 | -1.35e+5 | 4.76e+3 | 2.25e+4 | -3107.8 | -1015.2 | 315.35 | -30.84 |
Вопросы Дифф. Зачета по теме «гамма-функция».
Вычислить, используя свойства гамма-функции и её значения 
