2. Для установившегося течения идеальной несжимаемой жидкости имеет место уравнение Бернулли
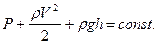
где r - плотность жидкости, V - скорость движения жидкости в данном сечении трубы, h - высота данного сечения трубы над некоторым уровнем, Р - статическое давление.
3. Скорость V истечения жидкости из малого отверстия, находящегося на глубине h относительно уровня жидкости в сосуде
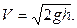
4. Сила сопротивления, испытываемая шариком при падении в вязкой жидкости (формула Стокса)
F = 6 p h rV,
где h - коэффициент внутреннего трения жидкости, r - радиус шарика, V - его скорость.
5. Характер движения жидкости (газа) определяется числом Рейнольдса
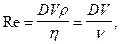
где h - динамическая вязкость жидкости (газа),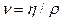 
- кинематическая вязкость, D - величина, характеризующая линейные размеры тела. Для потока жидкости в длинных трубах D - диаметр трубы, V - средняя по сечению скорость течения жидкости. Для движения шарика в жидкости D - диаметр шарика, V - скорость движения шарика.
При Re ≤ 1000 наблюдается ламинарное течение жидкости. Переход от ламинарного течения к турбулентному происходит в области 1000≤ Re≤2000. При Re = 2300 (для гладких труб) течение – турбулентное.
6. Объем жидкости (газа), протекающей за время t через длинную трубку длиной l (формула Пуазейля)
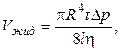
где R - радиус трубки, Dp - разность давлений на концах трубки, n - кинематическая вязкость.
1. Пренебрегая вязкостью жидкости, определить скорость истечения жидкости из малого отверстия в стенке сосуда, если высота уровня жидкости над отверстием составляет 1,5 м. (5,42 м/с)
2. В дне цилиндрического сосуда диаметром 0,5 м имеется круглое отверстие диаметром 1 см. Найти зависимость скорости понижения уровня воды в сосуде от высоты этого уровня и численное значение этой скорости для высоты уровня h = 0,2 м. (8´10-4 м/с)
3. На столе стоит сосуд с водой, в боковой поверхности которого имеется малое отверстие, расположенное на расстоянии 25 см от дна сосуда и на расстоянии 16 см от уровня воды. Уровень воды в сосуде поддерживается постоянным. На каком расстоянии от отверстия (по горизонтали) струя воды падает на стол? (40 см)
4. Цилиндрический бак высотою 1 м наполнен до краев водой. За какое время вся вода выльется через отверстие, расположенное у дна бака? Площадь поперечного сечения отверстия в 400 раз меньше площади поперечного сечения бака. (3 мин.)
5. Какое давление создает компрессор в краскопульте, если струя жидкой краски вытекает из него со скоростью 25 м/с? Плотность краски 0,8 г/см3. (2,5 атм)
6. Вода течет по цилиндрической трубе, причем за 1 с через ее поперечное сечение протекает 200 см3 воды. Динамическая вязкость воды в условиях опыта равна 0,001 Н´с/м2. Определить, при каком предельном значении диаметра трубы движение воды остается ламинарным. Считать, что ламинарность движения жидкости в цилиндрической трубе сохраняется при Re = 3000. (0,085 м)
7. В боковую поверхность сосуда вставлен горизонтальный капилляр, внутренний радиус которого 1 мм и длина 1,5 см. В сосуд налит глицерин, динамическая вязкость которого в условиях опыта равна 1,0 Н´с´м-2 Уровень глицерина в сосуде поддерживается постоянным на высоте 18 см выше капилляра. Сколько времени потребуется на то, чтобы из капилляра вытекло 5 см3 глицерина? (1,5 мин)
8. На столе стоит сосуд, в боковую поверхность которого вставлен горизонтальный капилляр на высоте 5 см от дна сосуда. Внутренний радиус капилляра 1 мм, длина 1 см. В сосуд налито машинное масло, плотность которого 900 кг/м3 и динамическая вязкость 0,5 Н´с´м-2. Уровень масла в сосуде поддерживается постоянным на высоте 50 см выше капилляра. Найти, на каком расстоянии от конца капилляра (по горизонтали) струя масла падает на стол. (0,011 м)
9. В боковую поверхность цилиндрического сосуда радиусом 2 см вставлен горизонтальный капилляр, внутренний радиус которого 1 мм и длина 2 см. В сосуд налито касторовое масло, динамическая вязкость которого в условиях опыта равна 12 г´см-1´с-1. Найти зависимость скорости понижения уровня касторового масла в сосуде от высоты этого уровня над капилляром. Найти численное значение этой скорости при высоте уровня над капилляром 26 см. (3´10-5 м/с)
10. Вода течет в горизонтально расположенной трубе переменного сечения. Скорость течения в широкой части трубы 20 см/с. Определить скорость течения воды в узкой части трубы, диаметр которой в 1,5 раза меньше диаметра широкой части. (0,45 м/с)
11. Какой наибольшей скорости может достичь дождевая капля диаметром 0,3 мм, если динамическая вязкость воздуха равна 1,2´10-4 г´см-1´с-1? (4,1 м/с)
12. Стальной шарик диаметром 1 мм падает с постоянной скоростью 0,185 см/с в большом сосуде, наполненном касторовым маслом. Найти динамическую вязкость касторового масла. (2 Н´с/м2)
13. Пробковый шарик радиусом 5 мм всплывает в большом сосуде, наполненном касторовым маслом. Определить динамическую и кинематическую вязкости касторового масла в условиях опыта, если шарик всплывает с постоянной скоростью 3,5 см/с. (1,09 Н´с/м2, 1,21´10-3 м2/с)
14. Смесь свинцовых дробинок диаметром 3 мм и 1 мм опустили в бак с глицерином глубиной 1 м. Какие дробинки упадут на дно позже? На сколько позже? Динамическая вязкость глицерина при температуре опыта 14,7 г´см-1´с-1. (на 4 мин)
15. В бочку заливается вода со скоростью 200 см3/с. На дне бочки образовалось отверстие площадью поперечного сечения 0,8 см2. Пренебрегая вязкостью воды, определить уровень воды в бочке. (31,9 см)
16. Шарик всплывает с постоянной скоростью в жидкости, плотность которой в 3 раза больше плотности материала шарика. Определить, во сколько раз сила трения, действующая на шарик, больше его веса. (2)
17. Стальной шарик диаметром 0,8 см падает с постоянной скоростью в касторовом масле с динамической вязкостью 0,99 Па´с. Определить характер движения масла, обусловленное падением в нем шарика, если критическое значение числа Рейнольдса 0,5. (турбулентное)
18. По трубе радиусом 1,5 см течет углекислый газ, плотность которого 7,5 кг/м3. Определить скорость течения газа, если за 20 минут через поперечное сечение трубы протекает 950 г газа. (0,15 м/с)
19. В сосуд заливается вода с постоянной скоростью 0,5 л/с. Пренебрегая вязкостью воды, определить диаметр отверстия в сосуде, при котором вода поддерживалось бы в нем на постоянном уровне h=20 см. (1,8 см)
20. Определить работу, которая затрачивается на преодоление трения при перемещении 1,5 м3 в горизонтальной трубе от сечения с давлением 40 кПа до сечения с давлением 20 кПа. (30 кДж)
21. В широкой части горизонтально расположенной трубы переменного сечения нефть течет со скоростью 2 м/с. Определить скорость течения нефти в узкой части трубы, если разность давлений в широкой и узкой частях трубы 50 мм рт.ст. Плотность нефти 900 кг/м3. (4,3 м/с)
22. В горизонтально расположенной трубе сечением 20 см2 течет жидкость. В одном месте труба имеет сужение сечением 12 см2. Разность уровней жидкости в двух манометрических трубках, установленных в широкой и узкой частях трубы, равна 8 см. Определить объемный расход жидкости. (1,9´10-3 м3/с)
23. Горизонтальный цилиндр насоса имеет диаметр 20 см. В нем движется со скоростью 1 м/с поршень, выталкивая воду через отверстие диаметром 2 см. С какой скоростью вода вытекает из отверстия? Каково избыточное давление воды в цилиндре? (100 м/с; 5 МН/м2)
24. Вода течет по круглой гладкой трубе диаметром 5 см со средней по сечению скоростью 10 см/с. Определить число Рейнольдса для потока жидкости в трубе и указать характер движения жидкости.(5000; движение турбулентное)
25. Бак высотой 2 м до краев заполнен жидкостью. На какой высоте должно быть проделано отверстие в стенке бака, чтобы место падения струи, вытекающей из отверстия, было на максимальном расстоянии от бака? (1 м)
26. Давление ветра на стену 200 Н/м2. Ветер дует перпендикулярно стене. Определить скорость ветра, если плотность воздуха 1,29 кг/м3.(17,4 м/с)
27. Струя воды диаметром 2 см, движущаяся со скоростью 10 м/с, ударяется о неподвижную плоскость, поставленную перпендикулярно к струе. Найти силу давления струи на плоскость, считая, что после удара о плоскость скорость частиц воды равна нулю. (31,4 Н)
28. К поршню спринцовки, расположенной горизонтально, приложена сила 15 Н. Определить скорость истечения воды из наконечника спринцовки, если площадь поршня 12 см2. (5 м/с)
29. В трубе с внутренним диаметром 3 см течет вода. Определить максимальный массовый расход воды при ламинарном течении. Считать, что ламинарность течения сохраняется при Re = 2300, вязкость воды считать равным 0,001 Па×с. (0,542 кг/с)
30. По трубе течет машинное масло. Максимальная скорость, при которой движение масла в этой трубе еще остается ламинарным, равна 3,2 см/с. При какой скорости движение глицерина в этой же трубе переходит от ламинарного к турбулентному? Считать плотность масла 900 кг/м3, вязкость масла – 0,5 Па×с. (0,048 м/с)
9 ЭЛЕМЕНТЫ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
1. Преобразования Лоренца
,
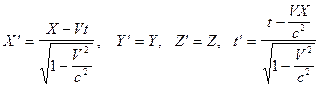где предполагается, что система отсчета К¢ движется со скоростью V в положительном направлении оси Х системы отсчета К, причем оси Х и Х¢ совпадают, а оси Y и Y¢ и Z и Z¢ параллельны . с - скорость распространения света в вакууме.
2. Длина l¢ тела, движущегося со скоростью V относительно некоторой системы отсчета К, связана с длиной l тела, неподвижного в этой системе, соотношением
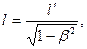
где b = V/с.
3. Промежуток времени t¢ в системе, движущейся относительно наблюдателя со скоростью V, связан с промежутком времени t в неподвижной для наблюдателя системе отсчета соотношением
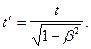
4. Релятивистский закон сложения скоростей.
Скорость тела u относительно неподвижной системы координат ХУZ связана со скоростью u¢ относительно движущейся со скоростью V системы координат Х¢Y¢Z¢ соотношением
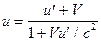
5. Зависимость массы тела от скорости его движения
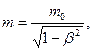
где m0 - масса покоя тела.
6. Полная энергия частицы Е прямо пропорциональна ее массе m:
E = mc 2 или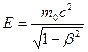 
.
Энергия покоя частицы
Ео = moc 2.