36 Фрактальная размерность
38 Методы моделирования процессов роста фрактальных структур
Процесс роста в природе может приводить к образованию расползающихся разреженных структур, называемых фрактальными. На примере одной из разновидностей фрактального роста можно объяснить такие непохожие физические явления, как образование кристаллов и движение воздушных пузырьков в жидкости
40 Перколяция
42 Методы получения фрактальных структур
В качестве первого примера рассмотрим более подробно образование фрактальных агрегатов кобальта. Малые частицы кобальта получали при испарении металла в атмосфере аргона при давлении 0,25-10 торр. Испарение металла осуществлялось с помощью нагретой вольфрамовой спирали. Конденсат металлических частиц в виде фрактальных образований собирался на медной сетке, покрытой углеродом. Средняя толщина металлического осадка составляла 10-200 мкм, причем относительный объем частиц кобальта в этом слое был в пределах 10- 2-10- 4, то есть осадок имел пористую структуру и основной объем занимали поры. Средний радиус частиц в этих образованиях увеличивался с ростом давления аргона. Фрактальная размерность агрегатов была в пределах 1,75-1,9 при давлении аргона в 0,9-8 торр, средний радиус частиц - менее 0,8 нм.
Фрактальные агрегаты могут быть получены также путем сжигания смеси в горящем пламени, если обеспечиваются условия конденсации и образования твердых частиц. Этот метод используется для получения фрактальных агрегатов SiO2 . С этой целью в водородно-кислородном пламени сжигался SiH4 . Образующийся при сжигании порошок содержит фрактальные агрегаты, состоящие из ї 103 частиц, радиус которых был в пределах 8-10 нм. Фрактальная размерность агрегатов D = 1,8-2,0. Сами частицы имели внутреннюю структуру, поскольку удельная поверхность образующихся частиц в 1,8-3,0 раза превышает поверхность частиц, являющихся сплошными. С ростом размера фрактального агрегата падают его плотность и прочность. Максимальный размер фрактальных агрегатов - микроны, а максимальное число частиц в них ї 104.
Полученные путем конденсации в газовой среде фрактальные агрегаты имеют очень высокую степень пористости. Объемная доля твердого вещества обычно составляет 10- 2-10- 4. Определение каких-либо свойств твердого тела становится при этом чрезвычайно затруднительным и в большинстве случаев даже невозможным. Поэтому актуальным является поиск способов и методов создания в твердых телах управляемой фрактальной структуры.
44 Открытые и закрытые системы. Линейные и нелинейные системы.
46 Эволюция нелинейных систем
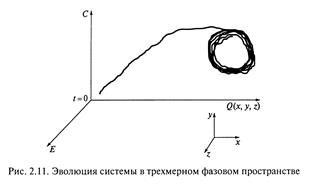
48 Понятие аттрактора
3 Принцип неопределённости Гейзенбе́рга в квантовой механике — фундаментальное неравенство (соотношение неопределённостей), устанавливающее предел точности одновременного определения пары характеризующих квантовую систему физических наблюдаемых (см. физическая величина), описываемых некоммутирующими операторами (например, координаты и импульса, тока и напряжения, электрического и магнитного поля). Соотношение неопределенностей[* 1] задаёт нижний предел для произведения среднеквадратичных отклонений пары квантовых наблюдаемых.
Если имеется несколько идентичных копий системы в данном состоянии, то измеренные значения координаты и импульса будут подчиняться определённому распределению вероятности — это фундаментальный постулат квантовой механики. Измеряя величину среднеквадратического отклонения Δx координаты и среднеквадратического отклонения Δp импульса, мы найдем что:
,
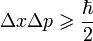где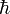 
— приведённая постоянная Планка.
§ В некоторых случаях «неопределённость» переменной определяется как наименьшая ширина диапазона, который содержит 50 % значений, что, в случае нормального распределения переменных, приводит для произведения неопределённостей к большей нижней границе .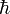
7 Тунне́льный эффект, туннели́рование — преодоление микрочастицей потенциального барьера в случае, когда её полная энергия (остающаяся при туннелировании неизменной) меньше высоты барьера. Туннельный эффект — явление исключительно квантовой природы, невозможное и даже полностью противоречащее классической механике. Аналогом туннельного эффекта в волновой оптике может служить проникновение световой волны внутрь отражающей среды (на расстояния порядка длины световой волны) в условиях, когда, с точки зрения геометрической оптики, происходит полное внутреннее отражение.
Туннельный эффект можно объяснить соотношением неопределённостей.[1] Записанное в виде:
,
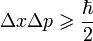оно показывает, что при ограничении квантовой частицы по координате, то есть увеличении её определённости по x, её импульс p становится менее определённым. Случайным образом неопределённость импульса Δp может добавить частице энергии для преодоления барьера. Таким образом, с некоторой вероятностью квантовая частица может проникнуть через барьер, а средняя энергия частицы останется неизменной.
9 При́нцип Па́ули (принцип запрета) — один из фундаментальных принципов квантовой механики, согласно которому два и более тождественных фермиона не могут одновременно находиться в одном квантовом состоянии.
11 Подвижность носителей заряда — коэффициент пропорциональности между дрейфовой скоростью носителей и приложенным внешним электрическим полем. Определяет способностьэлектронов и дырок в металлах и полупроводниках реагировать на внешнее воздействие.
Размерность подвижности м2/(В·с) или см2/(В·с). Фактически подвижность численно равна скорости носителей заряда при напряженности электрического поля в 1 В/м.
В анизотропной среде подвижность связывает компоненты дрейфовой скорости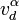 
с компонентами электрического поля Eβ
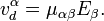
В простейшем случае изотропной и однородной среды можно записать
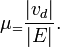
В модели Друде дрейфовая скорость с концентрацией определяют ток в системе
jα = enμEα = σEα.
И подвижность оказывается связанной с проводимостью системы
σ = enμ.
Для подвижности известно также следующее выражение, получаемое из кинетического уравнения в приближении времени релаксации :τ
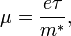
где m * — эффективная масса носителей.
13 В физике твёрдого тела, эффективной массой частицы называется динамическая масса, которая появляется при движении частицы в периодическом потенциале кристалла. Можно показать, что электроны и дырки в кристалле реагируют на электрическое поле так, как если бы они свободно двигались в вакууме, но с некой эффективной массой, которую обычно определяют в единицах массы покоя электрона me (9.11×10−31 кг). Она отлична от массы покоя электрона.
Эффективная масса определяется из аналогии со вторым законом Ньютона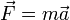 
. С помощью квантовой механики можно показать, что для электрона во внешнем электрическом полеE:
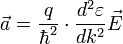
где a — ускорение, 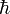— постоянная Планка, k — волновой вектор, который определяется из импульса как k = 
, 
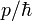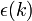— закон дисперсии, который связывает энергию с волновым вектором k. В присутствии электрического поля на электрон действует сила 
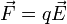, где заряд обозначен q. Отсюда можно получить выражение для эффективной массы m * :
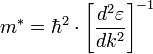
Для свободной частицы закон дисперсии квадратичен, и таким образом эффективная масса является постоянной и равной массе покоя. В кристалле ситуация более сложна и закон дисперсии отличается от квадратичного. В этом случае только в экстремумах кривой закона дисперсии, там где можно аппроксимировать параболой можно использовать понятие массы
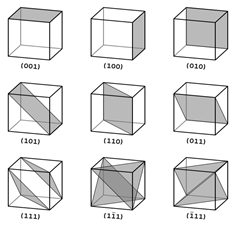17 Индексы Миллера — кристаллографические индексы, характеризующие расположение атомных плоскостей в кристалле. Индексы Миллера связаны с отрезками, отсекаемыми выбранной плоскостью на трёх осях кристаллографической системы координат (не обязательно декартовой). Таким образом, возможны три варианта относительного расположения осей и плоскости:
§ плоскость пересекает все три оси
§ плоскость пересекает две оси, а третьей параллельна
§ плоскость пересекает одну ось и параллельна двум другим
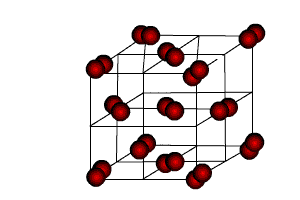25.Молекулярными называют кристаллические решётки, в узлах которых располагаются молекулы. Химические связи в них ковалентные, как полярные, так и неполярные. Связи в молекулах прочные, но между молекулами связи не прочные. Ниже представлена кристаллическая решётка I2
Вещества с МКР имеют малую твёрдость, плавятся при низкой температуре, летучие, при обычных условиях находятся в газообразном или жидком состоянии