Влияние температуры на вязкость газов[править | править исходный текст]

Дата: 2025-05-25; Просмотры: 3
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

В отличие от жидкостей, вязкость газов увеличивается с увеличением температуры (у жидкостей она уменьшается при увеличении температуры).

Формула Сазерленда может быть использована для определения вязкости идеального газа в зависимости от температуры:[1]

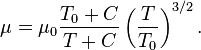
где:

· μ = динамическая вязкость в (Па·с) при заданной температуре T,

· μ0 = контрольная вязкость в (Па·с) при некоторой контрольной температуре T0,

· T = заданная температура в Кельвинах,

· T0 = контрольная температура в Кельвинах,

· C = постоянная Сазерленда для того газа, вязкость которого требуется определить.

Величина v/x называется градиентом скорости и показывает, как быстро меняется скорость при переходе от слоя к слою в направлении х, перпендикулярном направлению движения слоев

Теоретически, для хорошо отсортированного материала (песок мономиктовый) проницаемость не зависит от пористости.

Для реальных коллекторов в общем случае более пористые породы являются более проницаемыми.

Зависимость проницаемости от размера пор для фильтрации через капиллярные поры идеально пористой среды оценивается из соотношения уравнений Пуазейля и Дарси. В этом случае пористая среда представляется в виде системы прямых трубок одинакового сечения длиной L, равной длине пористой среды.

Уравнение Пуазейля описывает объёмную скорость течения жидкости через такую пористую среду:

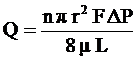, (1.22)

где r – радиус порового канала;

L – длина порового канала;

n – число пор, приходящихся на единицу площади фильтрации;

F – площадь фильтрации;

m – вязкость жидкости;

Все течения жидкости и газа качественно разделяются на 2 режима – ламинарный и турбулентный.

Ламинарное течение (lamina – пластинка, полоска) – это упорядоченное плавное течение жидкости, при котором жидкость перемещается как бы слоями, параллельными направлению течения (например – стенкам цилиндрической трубы), не перемешиваясь. Эти течения наблюдаются или у очень вязких жидкостей, или при малых скоростях течения, а также при течениях в узких трубках или при обтекании тел малых размеров.

Вообще тот или иной режим течения характеризуется числом Рейнольдса 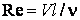, где V – характерная скорость течения, l – характерный линейный размер, 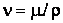– кинематический коэффициент вязкости; Re – безразмерный параметр.

Для каждого вида течения существует такое критическое число Рейнольдса, что при Re<Reкр возможно только ламинарное течение, в то время как при Re>Reкр течение может потерять устойчивость по отношению к малым возмущениям (случайным отклонениям) исходных параметров и стать турбулентным (например, для течения жидкости в цилиндрической трубе круглого поперечного сечения диаметром d Re = Vсрd/Ѕ – Reкр H 2300).

При турбулентном течении (turbulentus – беспорядочный, вихревой) частицы жидкости совершают неустановившиеся движения по сложным траекториям, что приводит к интенсивному перемешиванию между слоями жидкости, т.е. слоистая структура течения нарушается; при этом местные значения параметров движения – V, p, T,… испытывают хаотические флуктуации, т.е. случайные отклонения от средних значений, и изменяются нерегулярно во времени и пространстве.

Точное описание турбулентных течений весьма сложно, поэтому обычно для упрощения их условно заменяют фиктивными слоистыми течениями с некоторыми осредненными по времени скоростями 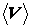, полагая 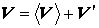, где 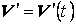–так называемая флуктуация или пульсация скорости, которая считается малой добавкой к 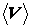, т.е. 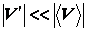; при этом фиктивное осредненное течение со скоростью 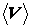часто можно считать установившимся, т.е. 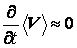, а само турбулентное течение – квазистационарным. Аналогично осредняются и другие термогазодинамические параметры: p = 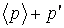, T =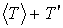

Число, или, правильнее, критерий Рейно́льдса ( 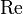), — безразмерная величина, характеризующая отношение нелинейного и диссипативного членов в уравнении Навье — Стокса[1]. Число Рейнольдса также считается критерием подобия течения вязкой жидкости.

Число Рейнольдса определяется следующим соотношением:

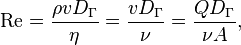
где

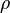· — плотность среды, кг/м3;

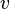· — характерная скорость, м/с;

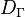· — гидравлический диаметр, м;

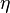· — динамическая вязкость среды, Н·с/м2;

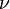· — кинематическая вязкость среды, м2/с ( );

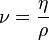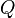· — объёмная скорость потока;

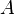· — площадь сечения трубы.

Для каждого вида течения существует критическое число Рейнольдса, 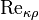, которое, как принято считать, определяет переход от ламинарного течения к турбулентному. При 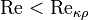течение происходит в ламинарном режиме, при 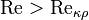возможно возникновение турбулентности. Критическое значение числа Рейнольдса зависит от конкретного вида течения (течение в круглой трубе, обтекание шара и т. п.), различными возмущениями потока, как-то изменение направленности и модуля вектора скорости потока, шероховатость стенок, близость местных сопротивлений и др. Например, для течения (точнее, для стабилизированного изотермического потока) жидкости в прямой круглой[источник не указан 688 дней] трубе с очень гладкими стенками 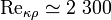. Для движения плёнки жидкости с относительно гладкой поверхностью раздела с газом при двухфазном потоке .

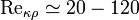Значения Re выше критического и до определённого предела относятся к переходному (смешанному) режиму течения жидкости, когда турбулентное течение более вероятно, но ламинарное иногда тоже наблюдается — то есть, неустойчивая турбулентность. Числу Reкр 2300 соответствует интервал 2300-10 000; для упомянутого примера с тонкими плёнками это 20-120 — 1600.

Число Рейнольдса как критерий перехода от ламинарного к турбулентному режиму течения и обратно относительно хорошо действует для напорных потоков. При переходе к безнапорным потокам переходная зона между ламинарным и турбулентным режимами возрастает, и использование числа Рейнольдса как критерия не всегда правомерно. Например, вводохранилищах формально вычисленные значения числа Рейнольдса очень велики, хотя там наблюдается ламинарное течение. Напротив, возмущения потока могут значительно снижать величину .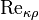

Стоит отметить, что для газов Reкр достигается при значительно бо́льших скоростях, чем у жидкостей, поскольку у первых куда больше кинематическая вязкость (в 10-15 раз).

Критерий назван в честь выдающегося английского физика О. Рейнольдса (1842—1912), автора многочисленных пионерских работ по гидродинамике.

1. Метод Короткова (механический)

Этот метод разработан русским хирургом Н.С.Коротковым в 1905 году. Для измерения давления предусмотрен очень простой прибор, состоящий из механического манометра, манжеты с грушей и фонендоскопа. Метод основан на полном пережатии манжетой плечевой артерии и выслушивании тонов, возникающих при медленном выпускании воздуха из манжеты.

Этот метод применяется в основном в профессиональной медицине, так как без специального обучения могут допускаться погрешности в показателях.

У этого метода есть как преимущества, так и недостатки.

К преимуществам относится тот факт, что метод Короткова признан официальным эталоном неинвазивного измерения артериального давления для диагностических целей и при проведении верификации автоматических измерителей артериального давления. Также для метода Короткова характерна высокая устойчивость к движениям руки.

К недостаткам метода Короткова можно отнести зависимость от индивидуальных особенностей человека, производящего измерение (хорошее зрение, слух, координация системы "руки-зрение-слух"). Метод Короткова чувствителен к шумам в помещении, точности расположения головки фонендоскопа относительно артерии. Для измерения давления по методу Короткова требуется непосредственный контакт манжеты и головки фонендоскопа с кожей пациента. Однако, метод измерения Короткова технически не сложен и обучение можно провести самостоятельно, следуя инструкции, приложенной к тонометру.